Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-26T18:55:19.139Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamics of the interaction of synthetic jet vortex rings with a stratified interface

Published online by Cambridge University Press:  06 June 2022

Lei Wang  and
Li-Hao Feng Open the ORCID record for Li-Hao Feng [Opens in a new window]
Lei Wang
Affiliation:
Fluid Mechanics Key Laboratory of Education Ministry, Beijing University of Aeronautics and Astronautics, Beijing 100191, PR China
Li-Hao Feng*
Affiliation:
Fluid Mechanics Key Laboratory of Education Ministry, Beijing University of Aeronautics and Astronautics, Beijing 100191, PR China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

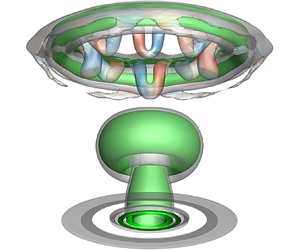
The vortex dynamics in a stratified environment is of fundamental importance in various flow systems, however, the mechanism of successive vortex–interface interactions remains not fully understood. This study investigates synthetic jet vortex rings impinging on a water–oil interface by experiment and numerical simulation. Two cases in the laminar and transitional regimes are concerned with the Froude number (Fr) of 0.35 and 0.82, respectively. The vortex rings for the two cases follow a similar evolution with three distinct stages, including vortex free-travel, vortex–interface interaction and vortex stretching. As products of the vortex–interface interaction, the secondary vortex rings are baroclinically generated in both water and oil followed by the formation of hairpin vortices through azimuthal deformation. Distinguished from an isolated vortex–interface interaction, complex interactions occur between the primary vortex ring and hairpin vortices, which can enhance the vortex ring instability in existence of the stratification for the laminar case. However, the vortex ring instability for the transitional case can develop earlier due to nonlinear effects with increasing Reynolds number. The spatio-temporal properties of the interface deformation and interfacial waves are analysed. The maximum penetration height of vortex rings scales with Fr2 as that for the isolated situation. Particularly, the transitional case is found to produce destabilization of the interfacial waves at a further radial location. The mechanism is revealed by connecting the dynamics of the vortex and the interface, which can be attributed to the radial development of perturbances stemming from the vortex ring instability under strong vortex–interface interaction.

JFM classification

Vortex Flows: Vortex dynamics Geophysical and Geological Flows: Stratified flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 943 , 25 July 2022 , A1
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Advaith, S., Manu, K.V., Tinaikar, A., Chetia, U.K. & Basu, S. 2017 Interaction of vortex ring with a stratified finite thickness interface. Phys. Fluids 29 (9), 093602.CrossRefGoogle Scholar
Archer, P.J., Thomas, T.G. & Coleman, G.N. 2008 Direct numerical simulation of vortex ring evolution from the laminar to the early turbulent regime. J. Fluid Mech. 598, 201–226.CrossRefGoogle Scholar
Archer, P.J., Thomas, T.G. & Coleman, G.N. 2010 The instability of a vortex ring impinging on a free surface. J. Fluid Mech. 642, 79–94.CrossRefGoogle Scholar
Brackbill, J., Kothe, D.B. & Zemach, C. 1992 A continuum method for modeling surface tension. J. Comput. Phys. 100 (2), 335–354.CrossRefGoogle Scholar
Brancher, P., Chomaz, J.M. & Huerre, P. 1994 Direct numerical simulations of round jets: vortex induction and side jets. Phys. Fluids 6 (5), 1768–1774.CrossRefGoogle Scholar
Cantwell, B. & Coles, D. 1983 An experimental study of entrainment and transport in the turbulent near wake of a circular cylinder. J. Fluid Mech. 136, 321–374.CrossRefGoogle Scholar
Cater, J.E. & Soria, J. 2002 The evolution of round zero-net-mass-flux jets. J. Fluid Mech. 472, 167–200.CrossRefGoogle Scholar
Cater, J.E., Soria, J. & Lim, T.T. 2004 The interaction of the piston vortex with a piston generated vortex ring. J. Fluid Mech. 499, 327–343.CrossRefGoogle Scholar
Champagnat, F., Plyer, A., Le Besnerais, G., Leclaire, B., Davoust, S. & Le Sant, Y. 2011 Fast and accurate PIV computation using highly parallel iterative correlation maximization. Exp. Fluids 50 (4), 1169–1182.CrossRefGoogle Scholar
Cheng, M., Lou, J. & Luo, L.S. 2010 Numerical study of a vortex ring impacting a flat wall. J. Fluid Mech. 660, 430–455.CrossRefGoogle Scholar
Chu, C.C., Wang, C.T. & Hsieh, C.S. 1993 An experimental investigation of vortex motions near surfaces. Phys. Fluids A: Fluid Dyn. 5 (3), 662–676.CrossRefGoogle Scholar
Cui, J. & Agarwal, R.W. 2006 Three-dimensional computation of a synthetic jet in quiescent air. AIAA J. 44 (12), 2857–2865.CrossRefGoogle Scholar
Dahm, W.J.A., Scheil, C.M. & Tryggvason, G. 1989 Dynamics of vortex interaction with a density interface. J. Fluid Mech. 205, 1–43.CrossRefGoogle Scholar
Das, D. & Arakeri, J.H. 1998 Transition of unsteady velocity profiles with reverse flow. J. Fluid Mech. 374, 251–283.CrossRefGoogle Scholar
Das, D. & Arakeri, J.H. 2000 Unsteady laminar duct flow with a given volume flow rate variation. J. Appl. Mech. 67(2), 274–281.CrossRefGoogle Scholar
Das, D., Bansal, M. & Manghnani, A. 2017 Generation and characteristics of vortex rings free of piston vortex and stopping vortex effects. J. Fluid Mech. 811, 138–167.CrossRefGoogle Scholar
Dazin, A., Dupont, P. & Stanislas, M. 2006 Experimental characterization of the instability of the vortex ring. Part II: non-linear phase. Exp. Fluids 41 (3), 401–413.CrossRefGoogle Scholar
Deng, J., Xue, J., Mao, X. & Caulfield, C.P. 2017 Coherent structures in interacting vortex rings. Phys. Rev. Fluids 2 (2), 022701.CrossRefGoogle Scholar
Derakhti, M. & Kirby, J.T. 2014 Bubble entrainment and liquid-bubble interaction under unsteady breaking waves. J. Fluid Mech. 761, 464–506.CrossRefGoogle Scholar
Gao, L., Wang, X., Yu, S.C.M. & Chyu, M.K. 2020 Development of the impulse and thrust for laminar starting jets with finite discharged volume. J. Fluid Mech. 902, A27.CrossRefGoogle Scholar
Ge, X., Vasilyev, O.V. & Hussaini, M.Y. 2019 Wavelet-based adaptive delayed detached eddy simulations for wall-bounded compressible turbulent flows. J. Fluid Mech. 873, 1116–1157.CrossRefGoogle Scholar
Glezer, A. 1988 The formation of vortex rings. Phys. Fluids 31 (12), 3532–3542.CrossRefGoogle Scholar
Glezer, A. & Amitay, M. 2002 Synthetic jets. Annu. Rev. Fluid Mech. 34, 503–529.CrossRefGoogle Scholar
Gritskevich, M.S., Garbaruk, A.V., Schütze, J. & Menter, F.R. 2012 Development of DDES and IDDES formulations for the shear stress transport model. Flow Turbul. Combust. 88 (3), 431–449.CrossRefGoogle Scholar
Hadžiabdić, M. & Hanjalić, K. 2008 Vortical structures and heat transfer in a round impinging jet. J. Fluid Mech. 596, 221–260.CrossRefGoogle Scholar
Herault, J., Facchini, G. & Bars, M.L. 2018 Erosion of a sharp density interface by a turbulent jet at moderate Froude and Reynolds numbers. J. Fluid Mech. 838, 631–657.CrossRefGoogle Scholar
Kambe, T. & Mya Oo, U. 1984 An axisymmetric viscous vortex motion and its acoustic emission. J. Phys. Soc. Japan 53 (7), 2263–2273.CrossRefGoogle Scholar
Kotapati, R.B., Mittal, R. & Cattafesta, L.N. III 2007 Numerical study of a transitional synthetic jet in quiescent external flow. J. Fluid Mech. 581, 287–321.CrossRefGoogle Scholar
Krueger, P.S. 2005 An over-pressure correction to the slug model for vortex ring circulation. J. Fluid Mech. 545, 427–443.CrossRefGoogle Scholar
Lin, H., Xiang, Y., Xu, H., Liu, H. & Zhang, B. 2020 Passive scalar mixing induced by the formation of compressible vortex rings. Acta Mechanica Sin. 36 (6), 1258–1274.CrossRefGoogle Scholar
Linden, P.F. 1973 The interaction of a vortex ring with a sharp density interface: a model for turbulent entrainment. J. Fluid Mech. 60, 467–480.CrossRefGoogle Scholar
Mansouri, Z. & Boushaki, T. 2019 Investigation of large-scale structures of annular swirling jet in a non-premixed burner using delayed detached eddy simulation. Intl J. Heat Fluid Flow 77, 217–231.CrossRefGoogle Scholar
Maxworthy, T. 1977 Some experimental studies of vortex rings. J. Fluid Mech. 81, 465–495.CrossRefGoogle Scholar
Mohasan, M., Aqeel, A.B., Lv, P.Y., Yang, Y.T. & Duan, H.L. 2021 Cavity dynamics of water drop impact onto immiscible oil pool with different viscosity. Acta Mechanica Sin. 37 (3), 447–455.CrossRefGoogle Scholar
Morre, D.W. & Saffman, P.G. 1975 The instability of a straight vortex filament in a strain field. Proc. R. Soc. A 346 (1646), 413–425.Google Scholar
Naitoh, T., Fukuda, N., Gotoh, T., Yamada, H. & Nakajima, K. 2002 Experimental study of axial flow in a vortex ring. Phys. Fluids 14 (1), 143–149.CrossRefGoogle Scholar
Olsthoorn, J. & Dalziel, S.B. 2017 Three-dimensional visualization of the interaction of a vortex ring with a stratified interface. J. Fluid Mech. 820, 549–579.CrossRefGoogle Scholar
Orlandi, P., Egermann, P. & Hopfinger, E.J. 1998 Vortex rings descending in a stratified fluid. Phys. Fluids 10 (11), 2819–2827.CrossRefGoogle Scholar
Orlandi, P. & Verzicco, R. 1993 Vortex rings impinging on walls: axisymmetric and three-dimensional simulations. J. Fluid Mech. 256, 615–646.CrossRefGoogle Scholar
Park, K.H., Chinaud, M. & Angeli, P. 2016 Transition from stratified to non-stratified oil-water flows using a bluff body. Exp. Therm. Fluid Sci. 76, 175–184.CrossRefGoogle Scholar
Ren, H. & Lu, X.Y. 2015 Dynamics and instability of a vortex ring impinging on a wall. Commun. Comput. Phys. 18 (4), 1122–1146.CrossRefGoogle Scholar
Sarpkaya, T. 1996 Vorticity, free surface, and surfactants. Annu. Rev. Fluid Mech. 28, 83–128.CrossRefGoogle Scholar
Shariff, K. & Leonard, A. 1992 Vortex rings. Annu. Rev. Fluid Mech. 24, 235–279.CrossRefGoogle Scholar
Shariff, K., Verzicco, R. & Orlandi, P. 1994 A numerical study of three-dimensional vortex ring instabilities: viscous corrections and early nonlinear stage. J. Fluid Mech. 279, 351–375.CrossRefGoogle Scholar
Shusser, M. & Gharib, M. 2000 Energy and velocity of a forming vortex ring. Phys. Fluids 12 (3), 618–621.CrossRefGoogle Scholar
Shuster, J.M. & Smith, D.R. 2007 Experimental study of the formation and scaling of a round synthetic jet. Phys. Fluids 19 (4), 045109.CrossRefGoogle Scholar
Smith, B.L. & Glezer, A. 1998 The formation and evolution of synthetic jets. Phys. Fluids 10 (9), 2281–2297.CrossRefGoogle Scholar
Song, M., Bernal, L.P. & Tryggvason, G. 1992 Head-on collision of a large vortex ring with a free surface. Phys. Fluids A: Fluid Dyn. 4 (7), 1457–1466.CrossRefGoogle Scholar
Song, M., Choi, S. & Kim, D. 2021 Interactions of the interface of immiscible liquids with an impinging vortex ring. Phys. Fluids 33 (2), 022108.CrossRefGoogle Scholar
Spalart, P.R. 2009 Detached-eddy simulation. Annu. Rev. Fluid Mech. 41, 203–229.CrossRefGoogle Scholar
Stock, M.J., Dahm, W.J.A. & Tryggvason, G. 2008 Impact of a vortex ring on a density interface using a regularized inviscid vortex sheet method. J. Comput. Phys. 227 (21), 9021–9043.CrossRefGoogle Scholar
Sullivan, I.S., Niemela, J.J., Hershberger, R.E., Bolster, D. & Donnelly, R.J. 2008 Dynamics of thin vortex rings. J. Fluid Mech. 609, 319–347.CrossRefGoogle Scholar
Van Buren, T., Whalen, E. & Amitay, M. 2014 Vortex formation of a finite-span synthetic jet: effect of rectangular orifice geometry. J. Fluid Mech. 745, 180–207.CrossRefGoogle Scholar
Verzicco, R. & Orlandi, P. 1996 A finite-difference scheme for three-dimensional incompressible flows in cylindrical coordinates. J. Comput. Phys. 123 (2), 402–414.CrossRefGoogle Scholar
Walker, J.D.A., Smith, C.R., Cerra, A.W. & Doligalski, T.L. 1987 The impact of a vortex ring on a wall. J. Fluid Mech. 181, 99–140.CrossRefGoogle Scholar
Wang, J.J. & Feng, L.H. 2018 Flow control techniques and applications. Cambridge University Press.CrossRefGoogle Scholar
Wang, L., Feng, L.H. & Xu, Y. 2019 Laminar-to-transitional evolution of three-dimensional vortical structures in a low-aspect-ratio rectangular synthetic jet. Exp. Therm. Fluid Sci. 104, 129–140.CrossRefGoogle Scholar
Wang, B., Liu, J., Yang, Y.J. & Xiao, Z.X. 2020 Numerical studies of undulation control on dynamic stall for reverse flows. Acta Mechanica Sin. 36 (2), 290–305.CrossRefGoogle Scholar
Weigand, A. & Gharib, M. 1995 Turbulent vortex ring/free surface interaction. Trans. ASME J. Fluids Engng 117 (3), 374–381.CrossRefGoogle Scholar
Widnall, S.E., Bliss, D. & Tsai, C. 1974 The instability of short waves on a vortex ring. J. Fluid Mech. 66, 35–47.CrossRefGoogle Scholar
Wu, X.G., Huang, Z.W., Dai, X.W., Mclennan, J., Zhang, S.K. & Li, R. 2020 Detached eddy simulation of the flow field and heat transfer in cryogenic nitrogen jet. Intl J. Heat Mass Transfer 150, 119275.CrossRefGoogle Scholar
Xu, Y., He, G. S., Kulkarni, V. & Wang, J. J. 2017 Experimental investigation of influence of Reynolds number on synthetic jet vortex rings impinging onto a solid wall. Exp. Fluids 58 (1), 6.CrossRefGoogle Scholar
Yeo, K.W.B., Koh, J.Y., Long, J. & New, T.H. 2020 Flow transitions in collisions between vortex-rings and density interfaces. J. Vis. 23 (5), 783–791.CrossRefGoogle Scholar
Zhou, J., Adrian, R.J., Balachandar, S. & Kendall, T.M. 1999 Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 387, 353–396.CrossRefGoogle Scholar