Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-29T12:44:09.396Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamics of spatially localized states in transitional plane Couette flow

Published online by Cambridge University Press:  25 March 2019

Anton Pershin Open the ORCID record for Anton Pershin [Opens in a new window] ,
Cédric Beaume Open the ORCID record for Cédric Beaume [Opens in a new window]  and
Steven M. Tobias Open the ORCID record for Steven M. Tobias [Opens in a new window]
Anton Pershin*
Affiliation:
School of Mathematics, University of Leeds, Leeds LS2 9JT, UK
Cédric Beaume
Affiliation:
School of Mathematics, University of Leeds, Leeds LS2 9JT, UK
Steven M. Tobias
Affiliation:
School of Mathematics, University of Leeds, Leeds LS2 9JT, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Unsteady spatially localized states such as puffs, slugs or spots play an important role in transition to turbulence. In plane Couette flow, steady versions of these states are found on two intertwined solution branches describing homoclinic snaking (Schneider et al., Phys. Rev. Lett., vol. 104, 2010, 104501). These branches can be used to generate a number of spatially localized initial conditions whose transition can be investigated. From the low Reynolds numbers where homoclinic snaking is first observed (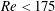$Re<175$) to transitional ones (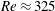$Re\approx 325$), these spatially localized states traverse various regimes where their relaminarization time and dynamics are affected by the dynamical structure of phase space. These regimes are reported and characterized in this paper for a 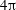$4\unicode[STIX]{x03C0}$-periodic domain in the streamwise direction as a function of the two remaining variables: the Reynolds number and the width of the localized pattern. Close to the snaking, localized states are attracted by spatially localized periodic orbits before relaminarizing. At larger values of the Reynolds number, the flow enters a chaotic transient of variable duration before relaminarizing. Very long chaotic transients (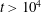$t>10^{4}$) can be observed without difficulty for relatively low values of the Reynolds number (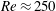$Re\approx 250$).

JFM classification

Nonlinear Dynamical Systems: Chaos Nonlinear Dynamical Systems: Pattern formation Instability: Transition to turbulence
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 867 , 25 May 2019 , pp. 414 - 437
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Avila, K., Moxey, D., de Lozar, A., Avila, M., Barkley, D. & Hof, B. 2011 The onset of turbulence in pipe flow. Science 333 (6039), 192–196.Google Scholar
Avila, M., Willis, A. P. & Hof, B. 2010 On the transient nature of localized pipe flow turbulence. J. Fluid Mech. 646, 127–136.Google Scholar
Barkley, D. 2016 Theoretical perspective on the route to turbulence in a pipe. J. Fluid Mech. 803, P1.Google Scholar
Barkley, D. & Tuckerman, L. S. 2005 Turbulent-laminar patterns in plane Couette flow. In IUTAM Symposium on Laminar-Turbulent Transition and Finite Amplitude Solutions, pp. 107–127. Springer.Google Scholar
Beaume, C., Bergeon, A. & Knobloch, E. 2013 Convectons and secondary snaking in three-dimensional natural doubly diffusive convection. Phys. Fluids 25 (2), 024105.Google Scholar
Beaume, C., Bergeon, A. & Knobloch, E. 2018 Three-dimensional doubly diffusive convectons: instability and transition to complex dynamics. J. Fluid Mech. 840, 74–105.Google Scholar
Bergeon, A. & Knobloch, E. 2008 Spatially localized states in natural doubly diffusive convection. Phys. Fluids 20, 034102.Google Scholar
Burke, J. & Dawes, J. H. P. 2012 Localized states in an extended Swift–Hohenberg equation. SIAM J. Appl. Dyn. Syst. 11 (1), 261–284.Google Scholar
Burke, J. & Knobloch, E. 2006 Localized states in the generalized Swift–Hohenberg equation. Phys. Rev. E 73 (5), 056211.Google Scholar
Chantry, M., Tuckerman, L. S. & Barkley, D. 2017 Universal continuous transition to turbulence in a planar shear flow. J. Fluid Mech. 824, R1.Google Scholar
Coullet, P., Riera, C. & Tresser, C. 2000 Stable static localized structures in one dimension. Phys. Rev. Lett. 84, 3069–3072.Google Scholar
Dauchot, O. & Daviaud, F. 1995 Finite amplitude perturbation and spots growth mechanism in plane Couette flow. Phys. Fluids 7 (2), 335–343.Google Scholar
Duguet, Y., Le Maître, O. & Schlatter, P. 2011 Stochastic and deterministic motion of a laminar-turbulent front in a spanwisely extended Couette flow. Phys. Rev. E 84 (6), 066315.Google Scholar
Duguet, Y. & Schlatter, P. 2013 Oblique laminar-turbulent interfaces in plane shear flows. Phys. Rev. Lett. 110, 034502.Google Scholar
Duguet, Y., Schlatter, P. & Henningson, D. S. 2009 Localized edge states in plane Couette flow. Phys. Fluids 21 (11), 111701.Google Scholar
Eckhardt, B., Schneider, T. M., Hof, B. & Westerweel, J. 2007 Turbulence transition in pipe flow. Annu. Rev. Fluid Mech. 39, 447–468.Google Scholar
Gibson, J. F.2014 Channelflow: a spectral Navier–Stokes simulator in C++. Tech. Rep., University of New Hampshire, Channelflow.org.Google Scholar
Gibson, J. F., Halcrow, J. & Cvitanović, P. 2009 Equilibrium and travelling-wave solutions of plane Couette flow. J. Fluid Mech. 638, 243–266.Google Scholar
Gibson, J. F. & Schneider, T. M. 2016 Homoclinic snaking in plane Couette flow: bending, skewing and finite-size effects. J. Fluid Mech. 794, 530–551.Google Scholar
Halcrow, J., Gibson, J. F., Cvitanović, P. & Viswanath, D. 2009 Heteroclinic connections in plane Couette flow. J. Fluid Mech. 621, 365–376.Google Scholar
Hamilton, J. M., Kim, J. & Waleffe, F. 1995 Regeneration mechanisms of near-wall turbulence structures. J. Fluid Mech. 287, 317–348.Google Scholar
Kawahara, G. & Kida, S. 2001 Periodic motion embedded in plane Couette turbulence: regeneration cycle and burst. J. Fluid Mech. 449, 291–300.Google Scholar
Knobloch, E. 2015 Spatial localization in dissipative systems. Annu. Rev. Condens. Matter Phys. 6 (1), 325–359.Google Scholar
Lemoult, G., Shi, L., Avila, K., Jalikop, S. V., Avila, M. & Hof, B. 2016 Directed percolation phase transition to sustained turbulence in Couette flow. Nat. Phys. 12 (3), 254–258.Google Scholar
Lloyd, D. J. B., Gollwitzer, C., Rehberg, C. & Richter, R. 2015 Homoclinic snaking near the surface instability of a polarizable fluid. J. Fluid Mech. 783, 283–305.Google Scholar
Mercader, I., Batiste, O., Alonso, A. & Knobloch, E. 2011 Convectons, anticonvectons and multiconvectons in binary fluid convection. J. Fluid Mech. 667, 586–606.Google Scholar
Meseguer, A. & Trefethen, L. N. 2003 Linearized pipe flow to Reynolds number 107 . J. Comput. Phys. 186, 178–197.Google Scholar
Nagata, M. 1990 Three-dimensional finite-amplitude solutions in plane Couette flow: bifurcation from infinity. J. Fluid Mech. 217, 519–527.Google Scholar
Olvera, D. & Kerswell, R. R. 2017 Optimizing energy growth as a tool for finding exact coherent structures. Phys. Rev. Fluids 2, 083902.Google Scholar
Orszag, S. A. 1971 Accurate solution of the Orr–Sommerfeld stability equation. J. Fluid Mech. 50, 689–703.Google Scholar
Pomeau, Y. 1986 Front motion, metastability and subcritical bifurcations in hydrodynamics. Physica D 23 (1–3), 3–11.Google Scholar
Romanov, V. A. 1973 Stability of plane-parallel Couette flow. Funct. Anal. Appl. 7 (2), 137–146.Google Scholar
Saarloos, W. V. 2003 Front propagation into unstable states. Phys. Rep. 386, 29–222.Google Scholar
Sano, M. & Tamai, K. 2016 A universal transition to turbulence in channel flow. Nat. Phys. 12 (3), 249–253.Google Scholar
Schmid, P. J. & Henningson, D. S. 2001 Stability and Transition in Shear Flows, vol. 142. Springer.Google Scholar
Schmiegel, A. & Eckhardt, B. 2000 Persistent turbulence in annealed plane Couette flow. Europhys. Lett. 51 (4), 395–400.Google Scholar
Schneider, T. M., Eckhardt, B. & Yorke, J. A. 2007 Turbulence transition and the edge of chaos in pipe flow. Phys. Rev. Lett. 99 (3), 034502.Google Scholar
Schneider, T. M., Gibson, J. F. & Burke, J. 2010a Snakes and ladders: localized solutions of plane Couette flow. Phys. Rev. Lett. 104 (10), 104501.Google Scholar
Schneider, T. M., Gibson, J. F., Lagha, M., De Lillo, F. & Eckhardt, B. 2008 Laminar-turbulent boundary in plane Couette flow. Phys. Rev. E 78 (3), 037301.Google Scholar
Schneider, T. M., Marinc, D. & Eckhardt, B. 2010b Localized edge states nucleate turbulence in extended plane Couette cells. J. Fluid Mech. 646, 441–451.Google Scholar
Shi, L., Avila, M. & Hof, B. 2013 Scale invariance at the onset of turbulence in Couette flow. Phys. Rev. Lett. 110 (20), 204502.Google Scholar
Skufca, J. D., Yorke, J. A. & Eckhardt, B. 2006 Edge of chaos in a parallel shear flow. Phys. Rev. Lett. 96 (17), 174101.Google Scholar
Viswanath, D. 2007 Recurrent motions within plane Couette turbulence. J. Fluid Mech. 580, 339–358.Google Scholar
Waleffe, F. 1997 On a self-sustaining process in shear flows. Phys. Fluids 9 (4), 883–900.Google Scholar
Waleffe, F. 2009 Turbulence and Interactions: Exact Coherent Structures in Turbulent Shear Flows. Springer.Google Scholar
Wang, J., Gibson, J. & Waleffe, F. 2007 Lower branch coherent states in shear flows: transition and control. Phys. Rev. Lett. 98 (20), 204501.Google Scholar
Willis, A. P. & Kerswell, R. R. 2007 Critical behavior in the relaminarization of localized turbulence in pipe flow. Phys. Rev. Lett. 98 (1), 014501.Google Scholar
Woods, P. D. & Champneys, A. R. 1999 Heteroclinic tangles and homoclinic snaking in the unfolding of a degenerate reversible Hamiltonian–Hopf bifurcation. Physica D 129, 147–170.Google Scholar