Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-23T18:09:56.292Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamics of sessile drops. Part 1. Inviscid theory

Published online by Cambridge University Press:  31 October 2014

J. B. Bostwick  and
P. H. Steen
J. B. Bostwick*
Affiliation:
Department of Engineering Science and Applied Mathematics Northwestern University, Evanston, IL 60208, USA
P. H. Steen
Affiliation:
Field of Theoretical and Applied Mechanics, Cornell University, Ithaca, NY 14853, USA School of Chemical and Biomolecular Engineering and Center for Applied Mathematics, Cornell University, Ithaca, NY 14853, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A sessile droplet partially wets a planar solid support. We study the linear stability of this spherical-cap base state to disturbances whose three-phase contact line is (i) pinned, (ii) moves with fixed contact angle and (iii) moves with a contact angle that is a smooth function of the contact-line speed. The governing hydrodynamic equations for inviscid motions are reduced to a functional eigenvalue problem on linear operators, which are parameterized by the base-state volume through the static contact angle and contact-line mobility via a spreading parameter. A solution is facilitated using inverse operators for disturbances (i) and (ii) to report frequencies and modal shapes identified by a polar 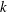$k$ and azimuthal 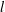$l$ wavenumber. For the dynamic contact-line condition (iii), we show that the disturbance energy balance takes the form of a damped-harmonic oscillator with ‘Davis dissipation’ that encompasses the dynamic effects associated with (iii). The effect of the contact-line motion on the dissipation mechanism is illustrated. We report an instability of the super-hemispherical base states with mobile contact lines (ii) that correlates with horizontal motion of the centre-of-mass, called the ‘walking’ instability. Davis dissipation from the dynamic contact-line condition (iii) can suppress the instability. The remainder of the spectrum exhibits oscillatory behaviour. For the hemispherical base state with mobile contact line (ii), the spectrum is degenerate with respect to the azimuthal wavenumber. We show that varying either the base-state volume or contact-line mobility lifts this degeneracy. For most values of these symmetry-breaking parameters, a certain spectral ordering of frequencies is maintained. However, because certain modes are more strongly influenced by the support than others, there are instances of additional modal degeneracies. We explain the physical reason for these and show how to locate them.

JFM classification

Waves/Free-surface Flows: Capillary waves Interfacial Flows (free surface): Contact lines Drops and Bubbles: Drops
Type
Papers
Information
Journal of Fluid Mechanics , Volume 760 , 10 December 2014 , pp. 5 - 38
Check for updates
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alabuzhev, A. A. & Lyubimov, D. V. 2007 Effect of the contact-line dynamics on the natural oscillations of a cylindrical droplet. J. Appl. Mech. Tech. Phys. 48 (5), 686–693.Google Scholar
Alabuzhev, A. A. & Lyubimov, D. V. 2012 Effect of the contact-line dynamics on the oscillations of a compressed droplet. J. Appl. Mech. Tech. Phys. 53 (1), 9–19.Google Scholar
Basaran, O. & DePaoli, D. 1994 Nonlinear oscillations of pendant drops. Phys. Fluids 6, 2923–2943.Google Scholar
Bostwick, J. B. & Steen, P. H. 2009 Capillary oscillations of a constrained liquid drop. Phys. Fluids 21, 032108.Google Scholar
Bostwick, J. B. & Steen, P. H. 2010 Stability of constrained cylindrical interfaces and the torus lift of Plateau–Rayleigh. J. Fluid Mech. 647, 201–219.Google Scholar
Bostwick, J. B. & Steen, P. H. 2013a Coupled oscillations of deformable spherical-cap droplets. Part 1. Inviscid motions. J. Fluid Mech. 714, 312–335.Google Scholar
Bostwick, J. B. & Steen, P. H. 2013b Coupled oscillations of deformable spherical-cap droplets. Part 2. Viscous motions. J. Fluid Mech. 714, 336–360.Google Scholar
Brunet, P., Eggers, J. & Deegan, R. D. 2009 Motion of a drop driven by substrate vibrations. Eur. Phys. J. Spec. Top. 166, 11–14.CrossRefGoogle Scholar
Brunet, P. & Snoeijer, J. H. 2011 Star-drops formed by periodic excitation and on an air cushion – a short review. Eur. Phys. J. Spec. Topics 192 (1), 207–226.Google Scholar
Celestini, F. & Kofman, R. 2006 Vibration of submillimeter-size supported droplets. Phys. Rev. E 73 (4), 041602.Google Scholar
Chandrasekhar, S. 1961 Hydrodynamic and Hydromagnetic Stability. Oxford University Press.Google Scholar
Chang, C. T.2013 Excited sessile drops perform harmonically, http://www.youtube.com/watch?v=Bk7xh4DqkiY, Published 23 November 2013.Google Scholar
Chang, C. T., Bostwick, J. B., Daniel, S. & Steen, P. H.2014 Dynamics of sessile drops. Part 2. Experiments (submitted).Google Scholar
Chang, C. T., Bostwick, J. B., Steen, P. H. & Daniel, S. 2013 Substrate constraint modifies the Rayleigh spectrum of vibrating sessile drops. Phys. Rev. E 88, 023015.Google Scholar
Chebel, N. A., Risso, F. & Masbernat, O. 2011 Inertial modes of a periodically forced buoyant drop attached to a capillary. Phys. Fluids 23 (10), 102104.Google Scholar
Courant, R. & Hilbert, D. 1953 Methods of Mathematical Physics, Vol. I. Wiley-Interscience Publications.Google Scholar
Daniel, S., Sircar, S., Gliem, J. & Chaudhury, M. K. 2004 Racheting motion of liquid drops on gradient surfaces. Langmuir 20, 4085–4092.CrossRefGoogle Scholar
Davis, S. H. 1980 Moving contact lines and rivulet instabilities. Part 1. The static rivulet. J. Fluid Mech. 98, 225–242.Google Scholar
DePaoli, W. D., Feng, J. Q., Basaran, O. A. & Scott, T. C. 1995 Hysteresis in forced oscillations of pendant drops. Phys. Fluids 7, 1181–1183.Google Scholar
Dong, L., Chaudhury, A. & Chaudhury, M. K. 2006 Lateral vibration of a water drop and its motion on a vibrating surface. Eur. Phys. J. E 21 (3), 231–242.Google Scholar
Dorbolo, S., Terwagne, D., Vandewalle, N. & Gilet, T. 2008 Resonant and rolling droplet. New J. Phys. 10 (11), 113021.Google Scholar
Dupré, A. 1869 Théorie Méchanique de La Chaleur. Gauthier-Villars.Google Scholar
Dussan, E. B. V. 1979 On the spreading of liquid on solid surfaces: static and dynamic contact lines. Annu. Rev. Fluid Mech. 11, 371–400.CrossRefGoogle Scholar
Faraday, M. 1831 On a peculiar class of acoustical figures, and on certain forms assumed by groups of particles upon vibrating elastic surfaces. Phil. Trans. R. Soc. Lond. 121, 299–340.Google Scholar
Fayzrakhmanova, I. S. & Straube, A. V. 2009 Stick–slip dynamics of an oscillated sessile drop. Phys. Fluids 21, 072104.CrossRefGoogle Scholar
Field, M., Golubitsky, M. & Stewart, I. 1991 Bifurcations on hemispheres. J. Nonlinear Sci. 1, 201–223.CrossRefGoogle Scholar
Hocking, L. M. 1987 The damping of capillary–gravity waves at a rigid boundary. J. Fluid Mech. 179, 253–266.Google Scholar
Ilyukhina, M. A. & Makov, Y. N. 2009 Analysis of shape perturbations of a drop on a vibrating substrate for different wetting angles. Acoust. Phys. 55 (6), 722–728.Google Scholar
James, A., Smith, M. K. & Glezer, A. 2003a Vibration-induced drop atomization and the numerical simulation of low-frequency single-droplet ejection. J. Fluid Mech. 476, 29–62.CrossRefGoogle Scholar
James, A., Vukasinovic, B., Smith, M. K. & Glezer, A. 2003b Vibration-induced drop atomization and bursting. J. Fluid Mech. 476, 1–28.CrossRefGoogle Scholar
Kreyszig, E. 1991 Differential Geometry. Dover.Google Scholar
Lamb, H. 1932 Hydrodynamics. Cambridge University Press.Google Scholar
Lanczos, C. 1986 The Variational Principles of Mechanics. Dover.Google Scholar
Lundgren, T. S. & Mansour, N. N. 1988 Oscillations of drops in zero gravity with weak viscous effects. J. Fluid Mech. 194, 479–510.Google Scholar
Lyubimov, D. V., Lyubimova, T. P. & Shklyaev, S. V. 2004 Non-axisymmetric oscillations of a hemispheric drop. Fluid Dyn. 39, 851–862.Google Scholar
Lyubimov, D. V., Lyubimova, T. P. & Shklyaev, S. V. 2006 Behavior of a drop on an oscillating solid plate. Phys. Fluids 18, 012101.CrossRefGoogle Scholar
MacRobert, T. M. 1967 Spherical Harmonics. Pergamon.Google Scholar
Miles, J. & Henderson, D. 1990 Parametrically forced surface waves. Annu. Rev. Fluid Mech. 22, 143–165.Google Scholar
Miller, C. A. & Scriven, L. E. 1968 The oscillations of a fluid droplet immersed in another fluid. J. Fluid Mech. 32, 417–435.Google Scholar
Milne, A. J. B., Defez, B., Cabrerizo-Vílchez, M. & Amirfazli, A. 2014 Understanding (sessile/constrained) bubble and drop oscillations. Adv. Colloid Interface Sci. 203, 22–36.Google Scholar
Myshkis, A. D., Babskii, V. G., Slobozhanin, N. D. & Tyuptsov, A. D. 1987 Low-Gravity Fluid Mechanics. Springer.Google Scholar
Noblin, X., Buguin, A. & Brochard-Wyart, F. 2004 Vibrated sessile drops: transition between pinned and mobile contact lines. Eur. Phys. J. E 14, 395–404.CrossRefGoogle Scholar
Noblin, X., Buguin, A. & Brochard-Wyart, F. 2005 Triplon modes of puddles. Phys. Rev. Lett. 94, 166102.Google Scholar
Noblin, X., Kofman, R. & Celestini, F. 2009 Ratchet-like motion of a shaken drop. Phys. Rev. Lett. 19, 194504.Google Scholar
Prosperetti, A. 1980 Normal-mode analysis for the oscillations of a viscous liquid drop in an immiscible liquid. J. Mec. 19, 149–182.Google Scholar
Prosperetti, A. 2012 Linear oscillations of constrained drops, bubbles and plane liquid surfaces. Phys. Fluids 24, 032109.Google Scholar
Ramalingam, S. K. & Basaran, O. A. 2010 Axisymmetric oscillation modes of a double droplet system. Phys. Fluids 22, 112111.CrossRefGoogle Scholar
Rayleigh, Lord 1879 On the capillary phenomenon of jets. Proc. R. Soc. Lond. 29, 71–97.Google Scholar
Segel, L. A. 1987 Mathematics Applied to Continuum Mechanics. Dover.Google Scholar
Sharp, J. S. 2012 Resonant properties of sessile droplets; contact angle dependence of the resonant frequency and width in glycerol/water mixtures. Soft Matt. 8, 399–407.CrossRefGoogle Scholar
Sharp, J. S., Farmer, D. J. & Kelly, J. 2011 Contact angle dependence of the resonant frequency of sessile water droplets. Langmuir 27 (15), 9367–9371.Google Scholar
Strani, M. & Sabetta, F. 1984 Free vibrations of a drop in partial contact with a solid support. J. Fluid Mech. 141, 233–247.Google Scholar
Taylor, J. R. 2005 Classical Mechanics. University Science Books.Google Scholar
Trinh, E. & Wang, T. G. 1982 Large-amplitude free and driven drop-shape oscillation: experimental results. J. Fluid Mech. 122, 315–338.Google Scholar
Tsamopoulos, J. A. & Brown, R. A. 1983 Nonlinear oscillations of inviscid drops and bubbles. J. Fluid Mech. 127, 519–537.Google Scholar
Vukasinovic, B., Smith, M. K. & Glezer, A. 2007 Dynamics of a sessile drop in forced vibration. J. Fluid Mech. 587, 395–423.CrossRefGoogle Scholar
Walter, J. 1973 Regular eigenvalue problems with eigenvalue parameter in the boundary condition. Math. Z. 133, 301–312.Google Scholar
Wang, T. G., Anilkumar, A. V. & Lee, C. P. 1996 Oscillations of liquid drops: results from USML-1 experiments in space. J. Fluid Mech. 308, 1–14.CrossRefGoogle Scholar
Weiland, R. H. & Davis, S. H. 1981 Moving contact lines and rivulet instabilities. Part 2. Long waves on flat rivulets. J. Fluid Mech. 107, 261–280.Google Scholar
Wilkes, E. & Basaran, O. 2001 Drop ejection from an oscillating rod. J. Colloid Interface Sci. 242, 180–201.Google Scholar
Yoshiyasu, N., Matsuda, K. & Takaki, R. 1996 Self-induced vibration of a water drop placed on an oscillating plate. J. Phys. Soc. Japan 65 (7), 2068–2071.CrossRefGoogle Scholar
Young, T. 1805 An essay on the cohesion of fluids. Phil. Trans. R. Soc. Lond. 95, 65–87.Google Scholar
Young, G. W. & Davis, S. H. 1987 Rivulet instabilities. J. Fluid Mech. 176, 1–31.Google Scholar