Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-23T05:41:56.281Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamics of non-circular finite-release gravity currents

Published online by Cambridge University Press:  22 October 2015

N. Zgheib ,
T. Bonometti  and
S. Balachandar
N. Zgheib
Affiliation:
Department of Mechanical and Aerospace Engineering, University of Florida, Gainesville, FL 32611, USA INPT, UPS, IMFT (Institut de Mécanique des Fluides de Toulouse), UMR 5502, Université de Toulouse, Allée Camille Soula, 31400 Toulouse, France
T. Bonometti*
Affiliation:
INPT, UPS, IMFT (Institut de Mécanique des Fluides de Toulouse), UMR 5502, Université de Toulouse, Allée Camille Soula, 31400 Toulouse, France
S. Balachandar
Affiliation:
Department of Mechanical and Aerospace Engineering, University of Florida, Gainesville, FL 32611, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The present work reports some new aspects of non-axisymmetric gravity currents obtained from laboratory experiments, fully resolved simulations and box models. Following the earlier work of Zgheib et al. (Theor. Comput. Fluid Dyn., vol. 28, 2014, pp. 521–529) which demonstrated that gravity currents initiating from non-axisymmetric cross-sectional geometries do not become axisymmetric, nor do they retain their initial shape during the slumping and inertial phases of spreading, we show that such non-axisymmetric currents eventually reach a self-similar regime during which (i) the local front propagation scales as 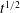$t^{1/2}$ as in circular releases and (ii) the non-axisymmetric front has a self-similar shape that primarily depends on the aspect ratio of the initial release. Complementary experiments of non-Boussinesq currents and top-spreading currents suggest that this self-similar dynamics is independent of the density ratio, vertical aspect ratio, wall friction and Reynolds number 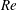$\mathit{Re}$, provided the last is large, i.e. 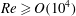$\mathit{Re}\geqslant O(10^{4})$. The local instantaneous front Froude number obtained from the fully resolved simulations is compared to existing models of Froude functions. The recently reported extended box model is capable of capturing the dynamics of such non-axisymmetric flows. Here we use the extended box model to propose a relation for the self-similar horizontal aspect ratio 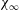${\it\chi}_{\infty }$ of the propagating front as a function of the initial horizontal aspect ratio 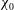${\it\chi}_{0}$, namely 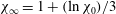${\it\chi}_{\infty }=1+(\ln {\it\chi}_{0})/3$. The experimental and numerical results are in good agreement with the proposed relation.

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Geophysical and Geological Flows: Gravity currents
Type
Papers
Information
Journal of Fluid Mechanics , Volume 783 , 25 November 2015 , pp. 344 - 378
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Allen, J. R. L. 1982 Sedimentary Structures: Their Character and Physical Basis. Elsevier.Google Scholar
Bagnold, R. A. 1941 The Physics of Blown Sand and Desert Dunes. Methuen.Google Scholar
Benjamin, T. 1968 Gravity currents and related phenomena. J. Fluid Mech. 31, 209–248.CrossRefGoogle Scholar
Bonometti, T. & Balachandar, S. 2008 Effect of Schmidt number on the structure and propagation of density currents. Theor. Comput. Fluid Dyn. 22, 341–361.Google Scholar
Bonometti, T., Balachandar, S. & Magnaudet, J. 2008 Wall effects in non-Boussinesq density currents. J. Fluid Mech. 616, 445–475.Google Scholar
Borden, Z. & Meiburg, E. 2013 Circulation based models for Boussinesq gravity currents. Phys. Fluids 25, 101301.CrossRefGoogle Scholar
Britter, R. E. & Simpson, J. E. 1978 Experiments on the dynamics of a gravity current head. J. Fluid Mech. 88, 223–240.Google Scholar
Cantero, M., Balachandar, S. & Garcia, M. 2007b High-resolution simulations of cylindrical density currents. J. Fluid Mech. 590, 437–469.CrossRefGoogle Scholar
Cantero, M., Lee, J. R., Balachandar, S. & Garcia, M. 2007a On the front velocity of gravity currents. J. Fluid Mech. 586, 1–39.Google Scholar
Canuto, C., Hussaini, M., Quarteroni, A. & Zang, T. 1988 Spectral Methods in Fluid Dynamics. Springer.CrossRefGoogle Scholar
Chakraborty, P., Balachandar, S. & Adrian, R. 2005 On the relationships between local vortex identification schemes. J. Fluid Mech. 535, 189–214.Google Scholar
Cortese, T. & Balachandar, S. 1995 High performance spectral simulation of turbulent flows in massively parallel machines with distributed memory. Int. J. Supercomput. Appl. 9, 187–204.Google Scholar
Dade, W. & Huppert, H. 1995 A box model for non-entraining suspension-driven gravity surges on horizontal surfaces. Sedimentology 42, 453–471.CrossRefGoogle Scholar
Didden, N. & Maxworthy, T. 1982 Viscous spreading of plane and axisymmetric gravity currents. J. Fluid Mech. 121, 27–42.CrossRefGoogle Scholar
Fannelop, T. & Waldman, G. 1971 The dynamics of oil slicks – or ‘creeping crude’. AIAA J. 41, 1–10.Google Scholar
Fay, J. 1969 The spreads of oil slicks on a calm sea. In Oils in the Sea (ed. Hoult, D. P.), pp. 53–63. Springer.CrossRefGoogle Scholar
Francis, P. 1993 Volcanoes: A Planetary Perspective (ed. Francis, P.). Clarendon.Google Scholar
Gladstone, C., Phillips, J. C. & Sparks, R. S. J. 1998. Experiments on bidisperse, constant-volume gravity currents: propagation and sediment deposition. Sedimentology 45, 833–844.CrossRefGoogle Scholar
Gutmark, E. J. & Grinstein, F. F. 1999 Flow control with noncircular jets. Annu. Rev. Fluid Mech. 31, 239–272.CrossRefGoogle Scholar
Härtel, C., Fredrik, C. & Mattias, T. 2000. Analysis and direct numerical simulation of the flow at a gravity-current head. Part 2. The lobe-and-cleft instability. J. Fluid Mech. 418, 213–229.Google Scholar
Hoult, D. P. 1972 Oil spreading on the sea. Annu. Rev. Fluid Mech. 4, 341–368.CrossRefGoogle Scholar
Huppert, H. E. 1982. Propagation of two-dimensional and axisymmetric viscous gravity currents over a rigid horizontal surface. J. Fluid Mech. 121, 43–58.Google Scholar
Huppert, H. & Simpson, J. 1980 The slumping of gravity currents. J. Fluid Mech. 99, 785–799.Google Scholar
Huq, P. 1996 The role of aspect ratio on entrainment rates of instantaneous, axisymmetric finite volume releases of density fluid. J. Hazard. Mater. 49, 89–101.Google Scholar
Kubat, M., Holte, R. C. & Matwin, S. 1998. Machine learning for the detection of oil spills in satellite radar images. Mach. Learn. 30, 195–215.CrossRefGoogle Scholar
List, E. J. 1982. Turbulent jets and plumes. Annu. Rev. Fluid Mech. 14, 189–212.Google Scholar
Lowe, D. R. 1982 Sediment gravity flows. Part II: depositional models with special reference to the deposits of high-density turbidity currents. J. Sedim. Res. 52, 279–297.Google Scholar
Quinn, W. R. 1989. On mixing in an elliptic turbulent free jet. Phys. Fluids A 1, 1716–1722.CrossRefGoogle Scholar
Rottman, J. W. & Simpson, J. E. 1983 Gravity currents produced by instantaneous releases of a heavy fluid in a rectangular channel. J. Fluid Mech. 135, 95–110.Google Scholar
Sahuri, R. M., Kaminski, A. K., Flynn, M. R. & Ungarish, M. 2015 Axisymmetric gravity currents in two-layer density-stratified media. Environ. Fluid Mech. 15, 1035–1051.Google Scholar
Simpson, J. E. 1972 Effects of the lower boundary on the head of a gravity current. J. Fluid Mech. 53, 759–768.CrossRefGoogle Scholar
Simpson, J. E. 1982 Gravity currents in the laboratory, atmosphere and oceans. Annu. Rev. Fluid Mech. 14, 213–234.CrossRefGoogle Scholar
Ungarish, M. 2009 An Introduction to Gravity Currents and Intrusions. CRC Press.Google Scholar
Ungarish, M. & Zemach, T. 2005 On the slumping of high Reynolds number gravity currents in two-dimensional and axisymmetric configurations. Eur. J. Mech. (B/Fluids) 24, 71–90.CrossRefGoogle Scholar
Unverdi, S. & Tryggvason, G. 1992 A front-tracking method for viscous, incompressible multi-fluid flows. J. Comput. Phys. 100, 25–37.CrossRefGoogle Scholar
Yarin, A. L. 2006 Drop impact dynamics: splashing, spreading, receding, bouncing …. Annu. Rev. Fluid Mech. 38, 159–192.CrossRefGoogle Scholar
Zgheib, N., Bonometti, T. & Balacandar, S. 2014 Long-lasting effect of initial configuration in gravitational spreading of material fronts. Theor. Comput. Fluid Dyn. 28, 521–529.Google Scholar
Zhou, J., Adrian, R., Balachandar, S. & Kendall, T. 1999 Mechanics for generating coherent packets of hairpin vortices. J. Fluid Mech. 387, 353–396.Google Scholar

Zgheib et al. supplementary movie

Cylindrical gravity current (Exp 1)

Download Zgheib et al. supplementary movie(Video)
Video 7 MB

Zgheib et al. supplementary movie

Cylindrical gravity current (Exp 1)

Download Zgheib et al. supplementary movie(Video)
Video 2.6 MB

Zgheib et al. supplementary movie

Cylindrical gravity current, top view (Exp 1)

Download Zgheib et al. supplementary movie(Video)
Video 3.7 MB

Zgheib et al. supplementary movie

Cylindrical gravity current, top view (Exp 1)

Download Zgheib et al. supplementary movie(Video)
Video 1.7 MB

Zgheib et al. supplementary movie

Non-circular gravity current (Exp 2)

Download Zgheib et al. supplementary movie(Video)
Video 6.8 MB

Zgheib et al. supplementary movie

Non-circular gravity current (Exp 2)

Download Zgheib et al. supplementary movie(Video)
Video 2.9 MB