Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-19T05:43:45.467Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamics of liquid films on vertical fibres in a radial electric field

Published online by Cambridge University Press:  02 July 2014

Zijing Ding ,
Jinlong Xie ,
Teck Neng Wong  and
Rong Liu
Zijing Ding*
Affiliation:
School of Mechanical and Aerospace Engineering, Nanyang Technological University, 639798, Republic of Singapore
Jinlong Xie
Affiliation:
School of Mechanical and Aerospace Engineering, Nanyang Technological University, 639798, Republic of Singapore
Teck Neng Wong*
Affiliation:
School of Mechanical and Aerospace Engineering, Nanyang Technological University, 639798, Republic of Singapore
Rong Liu
Affiliation:
Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, China
*
†Email addresses for correspondence: [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The long-wave behaviour of perfectly conducting liquid films flowing down a vertical fibre in a radial electric field was investigated by an asymptotic model. The validity of the asymptotic model was verified by the fully linearized problem, which showed that results were in good agreement in the long-wave region. The linear stability analysis indicated that, when the ratio (the radius of the outer cylindrical electrode over the radius of the liquid film) 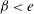$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\beta <e$, the electric field enhanced the long-wave instability; when 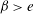$\beta >e$, the electric field impeded the long-wave instability; when 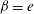$\beta =e$, the electric field did not affect the long-wave instability. The nonlinear evolution study of the asymptotic model compared well with the linear theory when 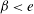$\beta <e$. However, when 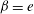$\beta =e$, the nonlinear evolution study showed that the electric field enhanced the instability which may cause the interface to become singular. When 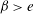$\beta >e$, the nonlinear evolution studies showed that the influence of the electric field on the nonlinear behaviour of the interface was complex. The electric field either enhanced or impeded the interfacial instability. In addition, an interesting phenomenon was observed by the nonlinear evolution study that the electric field may cause an oscillation in the amplitude of permanent waves when 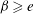$\beta \ge e$. Further study on steady travelling waves was conducted to reveal the influence of electric field on the wave speed. Results showed that the electric field either increased or decreased the wave speed as well as the wave amplitude and flow rate. In some situations, the wave speed may increase/decrease while its amplitude decreased/increased as the strength of the external electric field increased.

JFM classification

Interfacial Flows (free surface): Interfacial Flows (free surface) MHD and Electrohydrodynamics: MHD and Electrohydrodynamics Instability: Nonlinear instability
Type
Papers
Information
Journal of Fluid Mechanics , Volume 752 , 10 August 2014 , pp. 66 - 89
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Basset, A. 1894 Waves and jets in a viscous liquid. Am. J. Maths 16, 93–110.Google Scholar
Collins, R., Harris, M. & Basaran, O. 2007 Breakup of electrified jets. J. Fluid Mech. 588, 75–129.Google Scholar
Conroy, D., Matar, O., Craster, R. & Papageorgiou, D. 2011 Breakup of an electrified perfectly conducting, viscous thread in an AC field. Phys. Rev. E 83, 066314.Google Scholar
Craster, R. & Matar, O. 2006 On viscous beads flowing down a vertical fibre. J. Fluid Mech. 553, 85–105.Google Scholar
De Ryck, A. & Quéré, D. 1996 Inertial coating of a fiber. J. Fluid Mech. 311, 219–237.CrossRefGoogle Scholar
Ding, Z. & Liu, Q. 2011 Stability of liquid films on a porous vertical cylinder. Phys. Rev. E 84, 046307.Google Scholar
Ding, Z., Wong, T., Liu, R. & Liu, Q. 2013 Viscous liquid films on a porous vertical cylinder: dynamics and stability. Phys. Fluids 25, 064101.CrossRefGoogle Scholar
Duprat, C., Ruyer-Quil, C. & Giorgiutti-Dauphiné, F. 2009 Experimental study of the instability of a film flowing down a vertical fiber. Eur. Phys. J. Spec. Top. 166, 63–66.Google Scholar
Frenkel, A. 1992 Nonlinear thoery of strongly undulating thin films flowing down vertical cylinders. Europhys. Lett. 18, 583–588.Google Scholar
Goren, S. 1962 The instability of an annular thread of liquid. J. Fluid Mech. 12, 309–319.Google Scholar
Kliakhandler, I., Davis, S. & Bankhoff, S. 2001 Viscous beads on vertical fibre. J. Fluid Mech. 429, 381–390.Google Scholar
Lin, S. P. & Liu, W. C. 1975 Instability of film coating of wires and tubes. AIChE J. 21, 775–782.Google Scholar
Lister, J., Rallison, J., King, A., Cummings, L. & Jensen, O. 2006 Capillary drainage of an annular film: the dynamics of collars and lobes. J. Fluid Mech. 552, 311–343.Google Scholar
López-Herrera, J., Riesco-Chueca, P. & Gañón-Calvo, A. 2005 Linear stability analysis of axisymmetric perturbations in imperfectly conducting liquid jets. Phys. Fluids 17, 034106.Google Scholar
Pumir, A., Manneville, P. & Pomeau, Y. 1983 On solitary waves running down an inclined plane. J. Fluid Mech. 135, 27–50.Google Scholar
Quéré, D. 1990 Thin-films flowing on vertical fibers. Europhys. Lett. 13, 721–726.Google Scholar
Quéré, D. 1999 Fluid coating on a fiber. Annu. Rev. Fluid Mech. 31, 347–384.Google Scholar
Ruyer-Quil, C. & Kalliadasis, S. 2012 Wavy regimes of film flow down a fiber. Phys. Rev. E 85, 046302.CrossRefGoogle ScholarPubMed
Ruyer-Quil, C. & Manneville, P. 1998 Modeling Film flows down inclined planes. Eur. Phys. J. B 6, 277–292.Google Scholar
Ruyer-Quil, C., Treveleyan, P., Giorgiutti-Dauphiné, F. & Kalliadasis, S. 2008 Modeling film flows down a fibre. J. Fluid Mech. 603, 431–462.Google Scholar
Saville, D. 1971 Stability of electrically charged viscous cylinders. Phys. Fluids 14, 1095–1099.Google Scholar
Shkadov, V. Ya., Beloglazkin, A. & Gerasimov, S. 2008 Solitary waves in a viscous liquid film flowing down a thin vertical cylinder. Moscow Univ. Mech. Bull. 63, 122–128.Google Scholar
Sisoev, G., Craster, R., Matar, O. & Gerasimov, S. 2006 Film flow down a fibre at moderate flow rates. Chem. Engng Sci. 61, 7279–7298.Google Scholar
Son, P. & Ohba, K. 1998 Instability of a perfectly conducting liquid jet in electrohydrodynamic spraying: perturbation analysis and experimental verification. J. Phys. Soc. Japan 67, 825–832.CrossRefGoogle Scholar
Taylor, G. 1969 Electrically driven jets. Proc. R. Soc. Lond. A 313, 453–475.Google Scholar
Trifonov, Yu. Ya. 1992 Steady-state traveling waves on the surface of a viscous liquid film falling down on vertical wires and tubes. AIChE J. 38, 821–834.CrossRefGoogle Scholar
Wang, Q. 2012 Breakup of a poorly conducting liquid thread subject to a radial electric field at zero Reynolds number. Phys. Fluids 24, 102102.Google Scholar
Wang, Q., Mählmann, S. & Papageorgiou, D. 2009 Dynamics of liquid jets and threads under the action of radial electric fields: microthread formation and touchdown singularities. Phys. Fluids 21, 032109.Google Scholar
Wang, Q. & Papageorgiou, D. 2011 Dynamics of a viscous thread surrounded by another viscous fluid in a cylindrical tube under the action of a radial electric field: breakup and touchdown singularities. J. Fluid Mech. 683, 27–56.CrossRefGoogle Scholar
Wray, A., Matar, O. & Papageorgiou, D. 2012 Nonlinear waves in electrified viscous film flow down a vertical cylinder. IMA J. Appl. Maths 77, 430–440.CrossRefGoogle Scholar
Zuccher, S. 2008 Experimental investigations of the liquid-film instabilities forming on a wire under the action of a die. Intl J. Heat Fluid Flow 29, 1586–1592.Google Scholar