Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-29T18:55:36.889Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamics of large-scale circulation of turbulent thermal convection in a horizontal cylinder

Published online by Cambridge University Press:  06 February 2014

Hao Song ,
Eric Brown ,
Russell Hawkins  and
Penger Tong
Hao Song
Affiliation:
Department of Physics, Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong
Eric Brown
Affiliation:
Department of Mechanical Engineering and Materials Science, Yale University, New Haven, CT 06520, USA
Russell Hawkins
Affiliation:
School of Natural Sciences, University of California, Merced, CA 95343, USA
Penger Tong*
Affiliation:
Department of Physics, Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A systematic study of the effects of cell geometry on the dynamics of large-scale flows in turbulent thermal convection is carried out in horizontal cylindrical cells of different lengths filled with water. Four different flow modes are identified with increasing aspect ratio 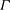$\Gamma $. For small aspect ratios (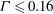$\Gamma \leq 0.16$), the flow is highly confined in a thin disc-like cell with a quasi-two-dimensional (quasi-2D) large-scale circulation (LSC) in the circular plane of the cell. For larger aspect ratios (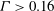$\Gamma >0.16$), we observe periodic switching of the angular orientation 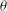$\theta $ of the rotation plane of LSC between the two longest diagonals of the cell. The sides of the container along which the LSC oscillates changes at a critical aspect ratio 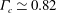$\Gamma _{c}\simeq 0.82$. The measured switching period is equal to the LSC turnover time for 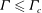$\Gamma \leq \Gamma _c$, shows a sharp increase at 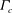$\Gamma _{c}$ and decays exponentially to the LSC turnover time with increasing 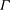$\Gamma $. For 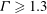$\Gamma \geq 1.3$, a periodic rocking of LSC along the long axis of the cylinder is also observed. The measured probability density function 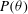$P(\theta )$ of the LSC orientation 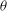$\theta $ peaks at the two diagonal positions, and its shape is described by a phenomenological model proposed by Brown & Ahlers (Phys. Fluids, vol. 20, 2008b, 075101; J. Fluid Mech., vol. 638, 2009, pp. 383–400). Using this model, we describe the dynamics of the LSC orientation 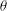$\theta $ by stochastic motion in a double-well potential. The potential is predicted from a model in which the sidewall shape produces an orientation-dependent pressure on the LSC. This model also captures key features of the four flow modes. The experiment reveals an interesting array of rich dynamics of LSC in the horizontal cylinders, which are very different from those observed in the upright cylindrical convection cells. The success of the model for both upright and horizontal cylinders suggests that it can be applied to different geometries.

JFM classification

Nonlinear Dynamical Systems: Low-dimensional models Turbulent Flows: Turbulent convection Turbulent Flows: Turbulent transition
Type
Papers
Information
Journal of Fluid Mechanics , Volume 740 , 10 February 2014 , pp. 136 - 167
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlers, G., Funfschilling, D. & Bodenschatz, E. 2009a Transitions in heat transport by turbulent convection at Rayleigh numbers up to $10^{15}$. New J. Phys. 11, 123001.CrossRefGoogle Scholar
Ahlers, G., Grossmann, S. & Lohse, D. 2009b Heat transfer and large-scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81 (2), 503–537.CrossRefGoogle Scholar
Arrhenius, S. 1889 On the reaction rate of the inversion of non-refined sugar upon souring. Z. Phys. Chem. 4, 226–248.Google Scholar
Belmonte, A., Tilgner, A. & Libchaber, A. 1993 Boundary layer length scales in thermal turbulence. Phys. Rev. Lett. 70, 4067–4070.Google Scholar
Brent, A. D., Voller, V. R. & Reid, K. J. 1988 Enthalpy-porosity technique for modelling convection-diffusion phase change application to the melting of a pure metal. Numer. Heat Transfer 13, 297–318.CrossRefGoogle Scholar
Brown, E. & Ahlers, G. 2006 Rotations and cessations of the large-scale circulation in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 568, 351–386.Google Scholar
Brown, E. & Ahlers, G. 2007 Large-scale circulation model for turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 98 (13), 134501.CrossRefGoogle ScholarPubMed
Brown, E. & Ahlers, G. 2008a Azimuthal asymmetries of the large-scale circulation in turbulent Rayleigh–Bénard convection. Phys. Fluids 20, 105105.Google Scholar
Brown, E. & Ahlers, G. 2008b A model of diffusion in a potential well for the dynamics of the large-scale circulation in turbulent Rayleigh–Bénard convection. Phys. Fluids 20, 075101.Google Scholar
Brown, E. & Ahlers, G. 2009 The origin of oscillations of the large-scale circulation of turbulent Rayleigh–Bénard convection. J. Fluid Mech. 638, 383–400.Google Scholar
Castaing, B., Gunaratne, G., Heslot, F., Libchaber, A., Kadanoff, L., Thomae, S., Wu, X., Zaleski, S. & Zanetti, G. 1989 Scaling of hards thermal turbulence in Rayleigh–Bénard convection. J. Fluid Mech. 204, 1–30.Google Scholar
Cattaneo, F., Emonet, T. & Weiss, N. 2003 On the interaction between convection and magnetic fields. Astrophys. J. 588, 1183–1198.Google Scholar
Chavanne, X., Chillà, F., Chabaud, B., Castaing, B. & Hébral, B. 2001 Turbulent Rayleigh–Bénard convection in gaseous and liquid He. Phys. Fluids 13, 1300.Google Scholar
Chillà, F. & Schumacher, J. 2012 New perspectives in turbulent Rayleigh–Bénard convection. Eur. Phys. J. E 35, 58.Google Scholar
Cioni, S., Ciliberto, S. & Sommeria, J. 1997 Strongly turbulent Rayleigh–Bénard convection in mercury: comparison with results at moderate Prandtl number. J. Fluid Mech. 335, 111–140.Google Scholar
Daya, Z. A. & Ecke, R. E. 2001 Does turbulent convection feel the shape of the container?. Phys. Rev. Lett. 87 (18), 184501.Google Scholar
Du, Y.-B. & Tong, P. 2000 Turbulent thermal convection in a cell with ordered rough boundaries. J. Fluid Mech. 407, 57–84.Google Scholar
Du, Y.-B. & Tong, P. 2001 Temperature fluctuations in a convection cell with rough upper and lower surfaces. Phys. Rev.E 63, 046303.Google Scholar
Dykman, M. I., Mannella, R., McClintock, P. V. E., Moss, F. & Soskin, S. M. 1988 Spectral density fluctuations of a double-well dung oscillator driven by white noise. Phys. Rev. A 37, 1303.Google Scholar
Funfschilling, D. & Ahlers, G. 2004 Plume motion and large-scale circulation in a cylindrical Rayleigh–Bénard cell. Phys. Rev. Lett. 92 (19), 194502.CrossRefGoogle Scholar
Funfschilling, D., Brown, E., Nikolaenko, A. & Ahlers, G. 2005 Heat transport by turbulent Rayleigh–Bénard convection in cylindrical samples with aspect ratio one and larger. J. Fluid Mech. 536, 145–154.Google Scholar
Gitterman, M. 2005 The Noisy Oscillator, The First Hundred Years, From Einstein Until Now. World Scientific.Google Scholar
Hanggi, P., Talkner, P. & Borkovec, M. 1990 Reaction rate theory: fifty years after Kramers. Rev. Mod. Phys. 62, 251–342.Google Scholar
Hartmann, D. L., Moy, L. A. & Fu, Q. 2001 Tropical convection and the energy balance at the top of the atmosphere. J. Clim. 14, 4495–4511.Google Scholar
He, X., Funfschilling, D., Nobach, H., Bodenschatz, E. & Ahlers, G. 2012 Transition to the ultimate state of turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 108, 024502.Google Scholar
Hunt, G. R. & Linden, P. F. 1999 The fluid mechanics of natural ventilation displacement ventilation by buoyancy-driven flows assisted by wind. Build. Environ. 34, 707–720.Google Scholar
Kadanoff, L. P. 2001 Turbulent heat flow: structures and scaling. Phys. Today 54, 34–39.Google Scholar
Kramers, H. A. 1940 Brownian motion in a field of force and the diffusion model of chemical reaction. Physica 7, 284–304.CrossRefGoogle Scholar
Lohse, D. & Xia, K.-Q. 2010 Small-scale properties of turbulent Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 42, 335–364.Google Scholar
Marshall, J. & Schott, F. 1999 Open-ocean convection: observations, theory, and models. Rev. Geophys. 37, 1–64.Google Scholar
McKenzie, D. P., Roberts, J. M. & Weiss, N. O. 1974 Convection in the Earths mantle: towards a numerical simulation. J. Fluid Mech. 62, 465–538.Google Scholar
Niemela, J. J., Skrbek, L., Sreenivasan, K. R. & Donnelly, R. J. 2000 Turbulent convection at very high Rayleigh numbers. Nature 404, 837–840.CrossRefGoogle ScholarPubMed
Niemela, J. J. & Sreenivasan, K. R. 2003 Rayleigh-number evolution of large-scale coherent motion in turbulent convection. Eur. Phys. Lett. 62, 829.Google Scholar
du Puits, R., Resagk, C. & Thess, A. 2007 Breakdown of wind in turbulent thermal convection. Phys. Rev. E 75, 016302.Google Scholar
du Puits, R., Resagk, C. & Thess, A. 2009 Structure of viscous boundary layers in turbulent Rayleigh–Bénard convection. Phys. Rev. E 63, 046303.Google Scholar
Qiu, X.-L., Shang, X.-D., Tong, P. & Xia, K.-Q. 2004 Velocity oscillations in turbulent Rayleigh–Bénard convection. Phys. Fluids 16, 412–423.Google Scholar
Qiu, X.-L. & Tong, P. 2001a Large-scale velocity structures in turbulent thermal convection. Phys. Rev. E 64 (3), 036304.Google Scholar
Qiu, X.-L. & Tong, P. 2001b Onset of coherent oscillations in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 87 (9), 094501.Google Scholar
Qiu, X.-L. & Tong, P. 2002 Temperature oscillations in turbulent Rayleigh–Bénard convection. Phys. Rev. E 66 (2), 026308.Google Scholar
Resagk, C., du Puits, R., Thess, A., Dolzhansky, F. V., Grossmann, S., Araujo, F. F. & Lohse, D. 2006 Oscillations of the large-scale wind in turbulent thermal convection. Phys. Fluids 18, 095105.Google Scholar
Settles, G. S. 2001 Schlieren and Shadowgraph Techniques: Visualizing Phenomena in Transparent Media. Springer.Google Scholar
Song, H.Effects of geometry on turbulent Rayleigh–Bénard convection. PhD thesis, Hong Kong University of Science and Technology.Google Scholar
Song, H. & Tong, P. 2010 Scaling laws in turbulent Rayleigh–Bénard convection under different geometry. Eur. Phys. Lett. 90, 44001.Google Scholar
Song, H., Villermaux, E. & Tong, P. 2011 Coherent oscillations of turbulent Rayleigh–Bénard convection in a thin vertical disk. Phys. Rev. Lett. 106, 184504.CrossRefGoogle Scholar
Sun, C., Cheung, Y. H. & Xia, K. Q. 2008 Experimental studies of the viscous boundary layer properties in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 605, 79–113.CrossRefGoogle Scholar
Sun, C., Ren, L. Y., Song, H. & Xia, K.-Q. 2005a Heat transport by turbulent Rayleigh–Bénard convection in 1m diameter cylindrical cells of widely varying aspect ratio. J. Fluid Mech. 542, 165–174.Google Scholar
Sun, C., Xia, K.-Q. & Tong, P. 2005b Three-dimensional flow structures and dynamics of turbulent thermal convection in a cylindrical cell. Phys. Rev. E 72 (2), 026302.Google Scholar
Sun, C., Zhou, Q. & Xia, K.-Q. 2006 Cascades of velocity and temperature fluctuations in buoyancy-driven thermal turbulence. Phys. Rev. Lett. 97, 144504.Google Scholar
Urban, P., Musilová, V. & Skrbek, L. 2011 Efficiency of heat transfer in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 107, 014302.Google Scholar
Villermaux, E. 1995 Memory-induced low frequency oscillations in closed convection boxes. Phys. Rev. Lett. 75 (25), 4618–4621.Google Scholar
Xi, H.-D. & Xia, K.-Q. 2007 Cessations and reversals of the large-scale circulation in turbulent thermal convection. Phys. Rev. E 75 (6), 066307.Google ScholarPubMed
Xi, H.-D., Zhou, Q. & Xia, K.-Q. 2006 Azimuthal motion of the mean wind in turbulent thermal convection. Phys. Rev. E 73 (5), 056312.Google ScholarPubMed
Xi, H.-D., Zhou, S.-Q., Zhou, Q., Chan, T.-S. & Xia, K.-Q. 2009 Origin of the temperature oscillation in turbulent thermal convection. Phys. Rev. Lett. 102 (4), 044503.Google Scholar
Xin, Y. B., Xia, K. Q. & Tong, P. 1996 Measured velocity boundary layers in turbulent convection. Phys. Rev. Lett. 77, 1266–1269.Google Scholar
Zhou, S. Q., Sun, C. & Xia, K.-Q. 2007 Measured oscillations of the velocity and temperature fields in turbulent Rayleigh–Bénard convection in a rectangular cell. Phys. Rev. E 76, 036301.Google Scholar
Zhou, Q., Xi, H. D., Zhou, S. Q., Sun, C. & Xia, K.-Q. 2009 Oscillations of the large-scale circulation in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 630, 367–390.Google Scholar
Zocchi, G., Moses, E. & Libchaber, A. 1990 Coherent structures in turbulent convection, an experimental study. Physica A 166, 387–407.CrossRefGoogle Scholar