Article contents
Dynamics of helicity in homogeneous skew-isotropic turbulence
Published online by Cambridge University Press: 25 May 2017
Abstract
The dynamics of helicity in homogeneous skew-isotropic freely decaying turbulence is investigated, at very high Reynolds numbers, thanks to a classical eddy-damped quasi-normal Markovian (EDQNM) closure. In agreement with previous direct numerical simulations, a 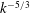 $k^{-5/3}$ inertial range is obtained for both the kinetic energy and helical spectra. In the early stage of the decay, when kinetic energy, initially only present at large scales cascades towards small scales, it is found that helicity slightly slows down the nonlinear transfers. Then, when the turbulence is fully developed, theoretical decay exponents are derived and assessed numerically for helicity. Furthermore, it is found that the presence of helicity does not modify the decay rate of the kinetic energy with respect to purely isotropic turbulence, except in Batchelor turbulence where the kinetic energy decays slightly more rapidly. In this case, non-local expansions are used to show analytically that the permanence of the large eddies hypothesis is verified for the helical spectrum, unlike the kinetic energy one. Moreover, the
$k^{-5/3}$ inertial range is obtained for both the kinetic energy and helical spectra. In the early stage of the decay, when kinetic energy, initially only present at large scales cascades towards small scales, it is found that helicity slightly slows down the nonlinear transfers. Then, when the turbulence is fully developed, theoretical decay exponents are derived and assessed numerically for helicity. Furthermore, it is found that the presence of helicity does not modify the decay rate of the kinetic energy with respect to purely isotropic turbulence, except in Batchelor turbulence where the kinetic energy decays slightly more rapidly. In this case, non-local expansions are used to show analytically that the permanence of the large eddies hypothesis is verified for the helical spectrum, unlike the kinetic energy one. Moreover, the 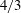 $4/3$ law for the two-point helical structure function is assessed numerically at very large Reynolds numbers. Afterwards, the evolution equation of the helicity dissipation rate is investigated analytically, which provides significant simplifications and leads notably to the definition of a helical derivative skewness and of a helical Taylor scale, which is numerically very close to the classical Taylor longitudinal scale at large Reynolds numbers. Finally, when both a mean scalar gradient and helicity are combined, the quadrature spectrum, linked to the antisymmetric part of the scalar flux, appears and scales like
$4/3$ law for the two-point helical structure function is assessed numerically at very large Reynolds numbers. Afterwards, the evolution equation of the helicity dissipation rate is investigated analytically, which provides significant simplifications and leads notably to the definition of a helical derivative skewness and of a helical Taylor scale, which is numerically very close to the classical Taylor longitudinal scale at large Reynolds numbers. Finally, when both a mean scalar gradient and helicity are combined, the quadrature spectrum, linked to the antisymmetric part of the scalar flux, appears and scales like 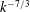 $k^{-7/3}$ and then like
$k^{-7/3}$ and then like 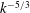 $k^{-5/3}$ in the inertial range.
$k^{-5/3}$ in the inertial range.
JFM classification
- Type
- Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 17
- Cited by



