Published online by Cambridge University Press: 11 April 2019
Continents exert a thermal blanket effect to the mantle underneath by locally accumulating heat and modifying the flow structures, which in turn affects continent motion. This dynamic feedback is studied numerically with a simplified model of an insulating plate over a thermally convecting fluid with infinite Prandtl number at Rayleigh numbers of the order of 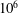 $10^{6}$. Several plate–fluid coupling modes are revealed as the plate size varies. In particular, small plates show long durations of stagnancy over cold downwellings. Between long stagnancies, bursts of velocity are observed when the plate rides on a single convection cell. As plate size increases, the coupled system transitions to another type of short-lived stagnancy, in which case hot plumes develop underneath. For an even larger plate, a unidirectional moving mode emerges as the plate modifies impeding flow structures it encounters while maintaining a single convection cell underneath. These identified modes are reminiscent of some real cases of continent–mantle coupling. Results show that the capability of a plate to overcome impeding flow structures increases with plate size, Rayleigh number and intensity of internal heating. Compared to cases with a fixed plate, cases with a freely drifting plate are associated with higher Nusselt number and more convection cells within the flow domain.
$10^{6}$. Several plate–fluid coupling modes are revealed as the plate size varies. In particular, small plates show long durations of stagnancy over cold downwellings. Between long stagnancies, bursts of velocity are observed when the plate rides on a single convection cell. As plate size increases, the coupled system transitions to another type of short-lived stagnancy, in which case hot plumes develop underneath. For an even larger plate, a unidirectional moving mode emerges as the plate modifies impeding flow structures it encounters while maintaining a single convection cell underneath. These identified modes are reminiscent of some real cases of continent–mantle coupling. Results show that the capability of a plate to overcome impeding flow structures increases with plate size, Rayleigh number and intensity of internal heating. Compared to cases with a fixed plate, cases with a freely drifting plate are associated with higher Nusselt number and more convection cells within the flow domain.