Published online by Cambridge University Press: 17 April 2015
The rotational motion of a prolate spheroidal particle suspended in shear flow is studied by a lattice Boltzmann method with external boundary forcing (LB-EBF). It has previously been shown that the case of a single neutrally buoyant particle is a surprisingly rich dynamical system that exhibits several bifurcations between rotational states due to inertial effects. It was observed that the rotational states were associated with either fluid inertia effects or particle inertia effects, which are always in competition. The effects of fluid inertia are characterized by the particle Reynolds number 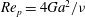 $\mathit{Re}_{p}=4Ga^{2}/{\it\nu}$, where
$\mathit{Re}_{p}=4Ga^{2}/{\it\nu}$, where 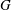 $G$ is the shear rate,
$G$ is the shear rate,  $a$ is the length of the particle major semi-axis and
$a$ is the length of the particle major semi-axis and  ${\it\nu}$ is the kinematic viscosity. Particle inertia is associated with the Stokes number
${\it\nu}$ is the kinematic viscosity. Particle inertia is associated with the Stokes number 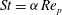 $\mathit{St}={\it\alpha}\,\mathit{Re}_{p}$, where
$\mathit{St}={\it\alpha}\,\mathit{Re}_{p}$, where  ${\it\alpha}$ is the solid-to-fluid density ratio. Previously, the neutrally buoyant case (
${\it\alpha}$ is the solid-to-fluid density ratio. Previously, the neutrally buoyant case (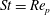 $\mathit{St}=\mathit{Re}_{p}$) was studied extensively. However, little is known about how these results are affected when
$\mathit{St}=\mathit{Re}_{p}$) was studied extensively. However, little is known about how these results are affected when 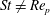 $\mathit{St}\neq \mathit{Re}_{p}$, and how the aspect ratio
$\mathit{St}\neq \mathit{Re}_{p}$, and how the aspect ratio 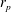 $r_{p}$ (major axis/minor axis) influences the competition between fluid and particle inertia in the absence of gravity. This work gives a full description of how prolate spheroidal particles in the range
$r_{p}$ (major axis/minor axis) influences the competition between fluid and particle inertia in the absence of gravity. This work gives a full description of how prolate spheroidal particles in the range 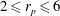 $2\leqslant r_{p}\leqslant 6$ behave depending on the chosen
$2\leqslant r_{p}\leqslant 6$ behave depending on the chosen 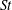 $\mathit{St}$ and
$\mathit{St}$ and 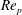 $\mathit{Re}_{p}$. Furthermore, consequences for the rheology of a dilute suspension containing such particles are discussed. Finally, grid resolution close to the particle is shown to affect the quantitative results considerably. It is suggested that this resolution is a major cause of quantitative discrepancies between different studies. Thus, the results of this work and previous direct numerical simulations of this problem should be regarded as qualitative descriptions of the physics involved, and more refined methods must be used to quantitatively pinpoint the transitions between rotational states.
$\mathit{Re}_{p}$. Furthermore, consequences for the rheology of a dilute suspension containing such particles are discussed. Finally, grid resolution close to the particle is shown to affect the quantitative results considerably. It is suggested that this resolution is a major cause of quantitative discrepancies between different studies. Thus, the results of this work and previous direct numerical simulations of this problem should be regarded as qualitative descriptions of the physics involved, and more refined methods must be used to quantitatively pinpoint the transitions between rotational states.