Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-26T22:32:22.278Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamic modelling of sea-surface roughness for large-eddy simulation of wind over ocean wavefield

Published online by Cambridge University Press:  30 May 2013

Di Yang ,
Charles Meneveau  and
Lian Shen
Di Yang
Affiliation:
Department of Mechanical Engineering, Johns Hopkins University, Baltimore, MD 21218, USA
Charles Meneveau
Affiliation:
Department of Mechanical Engineering, Johns Hopkins University, Baltimore, MD 21218, USA Center for Environmental and Applied Fluid Mechanics, Johns Hopkins University, Baltimore, MD 21218, USA
Lian Shen*
Affiliation:
Department of Mechanical Engineering, University of Minnesota, Minneapolis, MN 55455, USA St Anthony Falls Laboratory, University of Minnesota, Minneapolis, MN 55414, USA
*
†Email address for correspondence: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

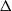Wind blowing over the ocean surface can be treated as a turbulent boundary layer over a multiscale rough surface with moving roughness elements, the waves. Large-eddy simulation (LES) of such flows is challenging because LES resolves wind–wave interactions only down to the grid scale, $\Delta $, while the effects of subgrid-scale (SGS) waves on the wind need to be modelled. Usually, a surface-layer model based on the law of the wall is used; but the surface roughness has been known to depend on the local wind and wave conditions and is difficult to parameterize. In this study, a dynamic model for the SGS sea-surface roughness is developed, with the roughness corresponding to the SGS waves expressed as 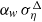${\alpha }_{w} \hspace{0.167em} { \sigma }_{\eta }^{\Delta } $. Here, 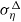${ \sigma }_{\eta }^{\Delta } $ is the effective amplitude of the SGS waves, modelled as a weighted integral of the SGS wave spectrum based on the geometric and kinematic properties of the waves for which five candidate expressions are examined. Moreover, 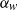${\alpha }_{w} $ is an unknown dimensionless model coefficient determined dynamically based on the first-principles constraint that the total surface drag force or average surface stress must be independent of the LES filter scale 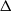$\Delta $. The feasibility and consistency of the dynamic sea-surface roughness models are assessed by a priori tests using data from high-resolution LES with near-surface resolution, appropriately filtered. Also, these data are used for a posteriori tests of the dynamic sea-surface roughness models in LES with near-surface modelling. It is found that the dynamic modelling approach can successfully capture the effects of SGS waves on the wind turbulence without ad hoc prescription of the model parameter 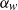${\alpha }_{w} $. Also, for 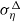${ \sigma }_{\eta }^{\Delta } $, a model based on the kinematics of wind–wave relative motion achieves the best performance among the five candidate models.

JFM classification

Turbulent Flows: Turbulence modelling Turbulent Flows: Turbulent boundary layers
Type
Papers
Information
Journal of Fluid Mechanics , Volume 726 , 10 July 2013 , pp. 62 - 99
Copyright
©2013 Cambridge University Press 

References

Albertson, J. D. & Parlange, M. B. 1999 Surface length scales and shear stress: implications for land–atmosphere interaction over complex terrain. Water Resour. Res. 35, 2121–2132.Google Scholar
Al-Zanaidi, M. A. & Hui, W. H. 1984 Turbulent airflow over water waves – a numerical study. J. Fluid Mech. 148, 225–246.Google Scholar
Anderson, W. & Meneveau, C. 2010 A large-eddy simulation model for boundary-layer flow over surfaces with horizontally resolved but vertically unresolved roughness elements. Boundary-Layer Meteorol. 137, 397–415.Google Scholar
Anderson, W. & Meneveau, C. 2011 Dynamic roughness model for large-eddy simulation of turbulent flow over multiscales, fractal-like rough surfaces. J. Fluid Mech. 679, 288–314.Google Scholar
Anderson, W., Passalacqua, P., Porté-Agel, F. & Meneveau, C. 2012 Large-eddy simulation of atmospheric boundary-layer flow over fluvial-like landscapes using a dynamic roughness model. Boundary-Layer Meteorol. 144, 263–286.Google Scholar
Belcher, S. E. & Hunt, J. C. R. 1993 Turbulent shear flow over slowly moving waves. J. Fluid Mech. 251, 109–148.Google Scholar
Belcher, S. E. & Hunt, J. C. R. 1998 Turbulent flow over hills and waves. Annu. Rev. Fluid Mech. 30, 507–538.CrossRefGoogle Scholar
Bou-Zeid, E., Meneveau, C. & Parlange, M. 2005 A scale-dependent Lagrangian dynamic model for large eddy simulation of complex turbulent flows. Phys. Fluids 17, 025105.CrossRefGoogle Scholar
Bou-Zeid, E., Parlange, M. B. & Meneveau, C. 2006 On the parameterization of surface roughness at regional scales. J. Atmos. Sci. 64, 216–227.CrossRefGoogle Scholar
Byrne, H. M. 1982 The variation of the drag coefficient in the marine surface layer due to temporal and spatial variations in the wind sea state. PhD thesis, University of Washington.Google Scholar
Calhoun, R. J., Street, R. J. & Koseff, J. R. 2001 Turbulent flow over a wavy surface: stratified case. J. Geophys. Res. 106, 9295–9310.CrossRefGoogle Scholar
Cartwright, D. E. 1963 The use of directional spectra in studying the output of a wave recorder on a moving ship. In Ocean Wave Spectra, pp. 203–218. Prentice Hall.Google Scholar
Caudal, G. 1993 Self-consistency between wind stress, wave spectrum, and wind-induced wave growth for fully rough air–sea interface. J. Geophys. Res. 98, 22743–22752.CrossRefGoogle Scholar
Cavaleri, L., Alves, J.-H. G. M., Ardhuin, F., Babanin, A., Banner, M., Belibassakis, K., Benoit, M., Donelan, M., Groeneweg, J., Herbers, T. H. C., Hwang, P., Jassen, P. A. E. M., Jassen, T., Lavrenov, I. V., Magne, R., Monbaliu, J., Onorato, M., Polnikov, V., Resio, D., Rogers, W. E., Sheremet, A., Smith, J. M., Tolman, H. L., van Vledder, G., Wolf, J. & Young, I. 2007 Wave modelling – the state of the art. Prog. Oceanogr. 75, 603–674.Google Scholar
Charnock, H. 1955 Wind stress on a water surface. Q. J. R. Meteorol. Soc. 81, 639–640.Google Scholar
Cohen, J. E. & Belcher, S. E. 1999 Turbulent shear flow over fast-moving waves. J. Fluid Mech. 386, 345–371.CrossRefGoogle Scholar
Deardorff, J. W. 1973 The use of subgrid transport equations in a three-dimensional model of atmospheric turbulence. Trans. ASME: J. Fluids Engng 95, 429–438.Google Scholar
Dobson, F. W. 1971 Measurements of atmospheric pressure on wind-generated sea waves. J. Fluid Mech. 48, 91–127.CrossRefGoogle Scholar
Dommermuth, D. G. & Yue, D. K. P. 1987 A high-order spectral method for the study of nonlinear gravity waves. J. Fluid Mech. 184, 267–288.Google Scholar
Donelan, M. A. 1990 Air–sea interaction. In The sea (ed. LeMehaute, B. & Hanes, D. M.), vol. 9, pp. 239–292. Wiley-Interscience.Google Scholar
Donelan, M. A. 1999 Wind-induced growth and attenuation of laboratory waves. In Wind-over-Wave Couplings: Perspectives and Prospects (ed. Aajjadi, S. G., Thomas, N. H. & Hunt, J. C. R.), pp. 183–194. Clarendon.Google Scholar
Donelan, M. A., Babanin, A. V., Young, I. R. & Banner, M. L. 2006 Wave-follower field measurements of the wind-input spectral function. Part II. Parameterization of the wind input. J. Phys. Oceanogr. 36, 1672–1689.Google Scholar
Drennan, W. M., Taylor, P. K. & Yelland, M. J. 2005 Parameterizing the sea surface roughness. J. Phys. Oceanogr. 35, 835–848.CrossRefGoogle Scholar
van Duin, C. A. & Janssen, P. A. E. M. 1992 A numerical model of the air flow above water waves. J. Fluid Mech. 236, 197–215.Google Scholar
Elliott, J. A. 1972 Microscale pressure fluctuations near waves being generated by the wind. J. Fluid Mech. 54, 427–448.CrossRefGoogle Scholar
Fairall, C. W., Bradley, E. F., Rogers, D. P., Edson, J. B. & Young, G. S. 1996 Bulk parameterization of air–sea fluxes for tropical ocean-glocal atmosphere coupled-ocean atmosphere response experiment. J. Geophys. Res. 101, 3747–3764.Google Scholar
Geernaert, G. L. 1983 Variation of the drag coefficient and its dependence on sea state. PhD thesis, University of Washington.Google Scholar
Gent, P. R. & Taylor, P. A. 1976 A numerical model of the air flow above water waves. J. Fluid Mech. 77, 105–128.Google Scholar
Germano, M., Piomelli, U., Moin, P. & Cabot, W. H. 1991 A dynamic subgrid-scale eddy viscosity model. Phys. Fluids A 3, 1760–1770.Google Scholar
Hasselmann, K., Barnett, T. P., Bouws, E., Carlson, H., Cartwright, D. E., Enke, K., Ewing, J. A., Gienapp, H., Hasselmann, D. E., Kruseman, P., Meerburg, A., Müller, P., Olbers, D. J., Richter, K., Sell, W. & Walden, H. 1973 Measurements of wind–wave growth and swell decay during the Joint North Sea Wave Project (JONSWAP). Dtsch. Hydrogr. Z. Suppl. 8 (12), 1–95.Google Scholar
Hasselmann, D. E., Dunckel, M. & Ewing, J. A. 1980 Directional wave spectra observed during JONSWAP 1973. J. Phys. Oceanogr. 10, 1264–1280.2.0.CO;2>CrossRefGoogle Scholar
Henn, D. S. & Sykes, R. I. 1999 Large-eddy simulation of flow over wavy surfaces. J. Fluid Mech. 383, 75–112.CrossRefGoogle Scholar
Hristov, T. S., Miller, S. D. & Friehe, C. A. 2003 Dynamical coupling of wind and ocean waves through wave-induced air flow. Nature 422, 55–58.Google Scholar
Hsu, S. A. 1974 A dynamic roughness equation and its application to wind stress determination at the air–sea interface. J. Phys. Oceanogr. 4, 116–120.Google Scholar
Janssen, P. A. E. M. 1991 Quasi-linear theory of wind–wave generation applied to wave forecasting. J. Phys. Oceanogr. 21, 1631–1642.2.0.CO;2>CrossRefGoogle Scholar
Janssen, P. 2004 The Interaction of Ocean Waves and Wind. Cambridge University Press.Google Scholar
Johnson, H. K., Høstrup, J., Vested, H. J. & Larsen, S. E. 1998 On the dependence of sea surface roughness on wind waves. J. Phys. Oceanogr. 28, 1702–1716.Google Scholar
Kihara, N., Hanazaki, H., Mizuya, T. & Ueda, H. 2007 Relationship between airflow at the critical height and momentum transfer to the traveling waves. Phys. Fluids 19, 015102.Google Scholar
Kincaid, D. & Cheney, W. 2001 Numerical Analysis: Mathematics of Scientific Computing, 3rd edn. Brooks Cole.Google Scholar
Kitaigorodskii, S. A. 1968 On the calculation of the aerodynamic roughness of the sea surface. Izv. Atmos. Ocean. Phys. 4, 870–878.Google Scholar
Kitaigorodskii, S. A. & Volkov, Y. A. 1965 On the roughness parameter of the sea surface and the calculation of momentum flux in the near water layer of the atmosphere. Bull. Acad. Sci. USSR Atmos. Ocean. Phys. 1, 973–988.Google Scholar
Kumar, V., Svensson, G., Holtslag, A. A. M., Meneveau, C. & Parlange, M. B. 2010 Impact of surface flux formulations and geostrophic forcing on large-eddy simulations of diurnal atmospheric boundary layer flow. J. Appl. Meteor. Climat. 49, 1496–1516.CrossRefGoogle Scholar
Lamb, H. 1932 Hydrodynamics. Dover.Google Scholar
Lettau, H. 1969 Note on aerodynamic roughness-parameter estimation on the basis of roughness-element description. J. Appl. Meteorol. 8, 828–832.Google Scholar
Lilly, D. K. 1992 A proposed modification of the Germano subgrid-scale closure method. Phys. Fluids A 4, 633–635.Google Scholar
Liu, Y., Yang, D., Guo, X. & Shen, L. 2010 Numerical study of pressure forcing of wind on dynamically evolving water waves. Phys. Fluids 22, 041704.Google Scholar
Longuet-Higgins, M. S. 1969 A nonlinear mechanism for the generation of sea waves. Proc. R. Soc. Lond. A 331, 371–389.Google Scholar
Makin, V. K., Kudryavtsev, V. N. & Mastenbroek, C. 1995 Drag of the sea surface. Boundary-Layer Meteorol. 73, 159–182.Google Scholar
Mastenbroek, C., Makin, V. K., Garat, M. H. & Giovanangeli, J. P. 1996 Experimental evidence of the rapid distortion of turbulence in the air flow over water waves. J. Fluid Mech. 318, 273–302.CrossRefGoogle Scholar
Mei, C. C., Stiassnie, M. & Yue, D. K. P. 2005 Theory and Applications of Ocean Surface Waves. Part 2: Nonlinear Aspects. World Scientific.Google Scholar
Miles, J. W. 1957 On the generation of surface waves by shear flows. J. Fluid Mech. 3, 185–204.Google Scholar
Miles, J. W. 1993 Surface-wave generation revisited. J. Fluid Mech. 256, 427–441.CrossRefGoogle Scholar
Moeng, H. 1984 A large-eddy simulation for the study of planetary boundary layer turbulence. J. Atmos. Sci. 41, 2052–2062.Google Scholar
Peirson, W. & Garcia, A. W. 2008 On the wind-induced growth of slow water waves of finite steepness. J. Fluid Mech. 608, 243–274.Google Scholar
Phillips, O. M. 1957 On the generation of waves by turbulent wind. J. Fluid Mech. 2, 417–445.Google Scholar
Piomelli, U. & Balaras, E. 2002 Wall-layer models for large-eddy simulations. Annu. Rev. Fluid Mech. 34, 349–374.Google Scholar
Plant, W. J. 1982 A relationship between wind stress and wave slope. J. Geophys. Res. 87, 1961–1967.CrossRefGoogle Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
Porté-Agel, F., Meneveau, C. & Parlange, M. B. 2000 A scale-dependent dynamic model for large-eddy simulation: application to a neutral atmospheric boundary layer. J. Fluid Mech. 415, 261–284.Google Scholar
Smith, S. D. 1988 Coefficients for sea surface wind stress, heat flux and wind profiles as a function of wind speed and temperature. J. Geophys. Res. 93, 15467–15472.Google Scholar
Smith, S. D., Anderson, R. J., Oost, W. A., Kraan, C., Maat, N., DeCosmo, J., Katsaros, K. B., Davidson, K. L., Bumke, K., Hasse, L. & Chadwick, H. M. 1992 Sea surface wind stress and drag coefficients: the HEXOS results. Boundary-Layer Meteorol. 60, 109–142.Google Scholar
Snyder, R. L., Dobson, F. W., Elliott, J. A. & Long, R. B. 1981 Array measurements of atmospheric pressure fluctuations above surface gravity waves. J. Fluid Mech. 102, 1–59.Google Scholar
Sullivan, P. P., Edson, J. B., Hristov, T. & McWilliams, J. C. 2008 Large-eddy simulations and observations of atmospheric marine boundary layers above nonequilibrium surface waves. J. Atmos. Sci. 65, 1225–1245.CrossRefGoogle Scholar
Sullivan, P. P. & McWilliams, J. C. 2010 Dynamics of winds and currents coupled to surface waves. Annu. Rev. Fluid Mech. 42, 19–42.CrossRefGoogle Scholar
Sullivan, P. P., McWilliams, J. C. & Hristov, T. 2010 A large eddy simulation model of high wind marine boundary layers above a spectrum of resolved moving waves. In 19th Conference on Boundary Layer and Turbulence, Keystone, CO.Google Scholar
Sullivan, P. P., McWilliams, J. C. & Moeng, C.-H. 2000 Simulation of turbulent flow over idealized water waves. J. Fluid Mech. 404, 47–85.Google Scholar
Taylor, P. K. & Yelland, M. J. 2001 The dependence of sea surface roughness on the height and steepness of the waves. J. Phys. Oceanogr. 31, 572–590.Google Scholar
Toba, Y., Smith, S. D. & Ebuchi, N. 2001 Historical drag expressions. In Wind Stress over the Ocean (ed. Jones, I. S. F. & Toba, Y.), pp. 35–53. Cambridge University Press.Google Scholar
Townsend, A. A. 1972 Flow in a deep turbulent boundary layer over a surface distorted by water waves. J. Fluid Mech. 55, 719–735.Google Scholar
West, B. J., Brueckner, K. A. & Janda, P. S. 1987 A new numerical method for surface hydrodynamics. J. Geophys. Res. 92, 11803–11824.Google Scholar
Wu, G. 2004 Direct simulation and deterministic prediction of large-scale nonlinear ocean wave-field. PhD thesis, Massachusetts Institute of Technology.Google Scholar
Yang, D. & Shen, L. 2009 Characteristics of coherent vortical structures in turbulent flows over progressive surface waves. Phys. Fluids 21, 125106.Google Scholar
Yang, D. & Shen, L. 2010 Direct-simulation-based study of turbulent flow over various waving boundaries. J. Fluid Mech. 650, 131–180.Google Scholar
Yang, D. & Shen, L. 2011a Simulation of viscous flows with undulatory boundaries. Part I. Basic solver. J. Comput. Phys. 230, 5488–5509.CrossRefGoogle Scholar
Yang, D. & Shen, L. 2011b Simulation of viscous flows with undulatory boundaries. Part II. Coupling with other solvers for two-fluid computations. J. Comput. Phys. 230, 5510–5531.Google Scholar
Yang, D., Shen, L. & Meneveau, C. 2013 An assessment of dynamic subgrid-scale sea-surface roughness models. Flow Turbul. Combust. doi:10.1007/s10494-013-9459-7.Google Scholar
Zakharov, V. E. 1968 Stability of periodic waves of finite amplitude on the surface of a deep fluid. J. Appl. Mech. Tech. Phys. 9, 190–194.Google Scholar