Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Soligno, Giuseppe
Dijkstra, Marjolein
and
van Roij, René
2014.
The equilibrium shape of fluid-fluid interfaces: Derivation and a new numerical method for Young’s and Young-Laplace equations.
The Journal of Chemical Physics,
Vol. 141,
Issue. 24,
p.
244702.
Yang, Luhang
Quan, Xiaojun
Cheng, Ping
and
Cheng, Zhiming
2014.
A free energy model and availability analysis for onset of condensation on rigid and liquid surfaces in moist air.
International Journal of Heat and Mass Transfer,
Vol. 78,
Issue. ,
p.
460.
Verma, Gopal
and
Singh, Kamal P.
2014.
Time-resolved interference unveils nanoscale surface dynamics in evaporating sessile droplet.
Applied Physics Letters,
Vol. 104,
Issue. 24,
Wang, Yumo
Dhong, Charles
and
Frechette, Joelle
2015.
Out-of-Contact Elastohydrodynamic Deformation due to Lubrication Forces.
Physical Review Letters,
Vol. 115,
Issue. 24,
Cao, Zhen
and
Dobrynin, Andrey V.
2015.
Polymeric Droplets on Soft Surfaces: From Neumann’s Triangle to Young’s Law.
Macromolecules,
Vol. 48,
Issue. 2,
p.
443.
Dervaux, Julien
and
Limat, Laurent
2015.
Contact lines on soft solids with uniform surface tension: analytical solutions and double transition for increasing deformability.
Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 471,
Issue. 2176,
p.
20140813.
Snoeijer, Jacco H.
and
van Wijngaarden, Leen
2015.
Interface deformations due to counter-rotating vortices: Viscous versus elastic media.
Physical Review E,
Vol. 91,
Issue. 3,
Nold, A.
Sibley, D. N.
Goddard, B. D.
Kalliadasis, S.
and
Nepomnyashchy, A. A.
2015.
Nanoscale Fluid Structure of Liquid-solid-vapour Contact Lines for a Wide Range of Contact Angles.
Mathematical Modelling of Natural Phenomena,
Vol. 10,
Issue. 4,
p.
111.
Karpitschka, S.
Das, S.
van Gorcum, M.
Perrin, H.
Andreotti, B.
and
Snoeijer, J. H.
2015.
Droplets move over viscoelastic substrates by surfing a ridge.
Nature Communications,
Vol. 6,
Issue. 1,
Dey, Ranabir
Daga, Ashish
DasGupta, Sunando
and
Chakraborty, Suman
2015.
Electrically modulated dynamic spreading of drops on soft surfaces.
Applied Physics Letters,
Vol. 107,
Issue. 3,
p.
034101.
Style, Robert W.
Isa, Lucio
and
Dufresne, Eric R.
2015.
Adsorption of soft particles at fluid interfaces.
Soft Matter,
Vol. 11,
Issue. 37,
p.
7412.
Jensen, Katharine E.
Sarfati, Raphael
Style, Robert W.
Boltyanskiy, Rostislav
Chakrabarti, Aditi
Chaudhury, Manoj K.
and
Dufresne, Eric R.
2015.
Wetting and phase separation in soft adhesion.
Proceedings of the National Academy of Sciences,
Vol. 112,
Issue. 47,
p.
14490.
Liu, Tianshu
Jagota, Anand
and
Hui, Chung-Yuen
2015.
Adhesive contact of a rigid circular cylinder to a soft elastic substrate – the role of surface tension.
Soft Matter,
Vol. 11,
Issue. 19,
p.
3844.
Lhermerout, Romain
Perrin, Hugo
Rolley, Etienne
Andreotti, Bruno
and
Davitt, Kristina
2016.
A moving contact line as a rheometer for nanometric interfacial layers.
Nature Communications,
Vol. 7,
Issue. 1,
Andreotti, Bruno
and
Snoeijer, Jacco H.
2016.
Soft wetting and the Shuttleworth effect, at the crossroads between thermodynamics and mechanics.
EPL (Europhysics Letters),
Vol. 113,
Issue. 6,
p.
66001.
Mehrabian, Hadi
Harting, Jens
and
Snoeijer, Jacco H.
2016.
Soft particles at a fluid interface.
Soft Matter,
Vol. 12,
Issue. 4,
p.
1062.
Sinha, Shayandev
and
Das, Siddhartha
2016.
Role of the Shuttleworth effect in adhesion on elastic surfaces.
MRS Advances,
Vol. 1,
Issue. 10,
p.
621.
Karpitschka, Stefan
van Wijngaarden, Leen
and
Snoeijer, Jacco H.
2016.
Surface tension regularizes the crack singularity of adhesion.
Soft Matter,
Vol. 12,
Issue. 19,
p.
4463.
Andreotti, Bruno
Bäumchen, Oliver
Boulogne, François
Daniels, Karen E.
Dufresne, Eric R.
Perrin, Hugo
Salez, Thomas
Snoeijer, Jacco H.
and
Style, Robert W.
2016.
Solid capillarity: when and how does surface tension deform soft solids?.
Soft Matter,
Vol. 12,
Issue. 12,
p.
2993.
Snoeijer, Jacco H.
2016.
Analogies between elastic and capillary interfaces.
Physical Review Fluids,
Vol. 1,
Issue. 6,
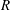 $R$, the molecular size
$R$, the molecular size  $a$ and the ratio of surface tension to elastic modulus
$a$ and the ratio of surface tension to elastic modulus 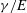 $\gamma /E$. We show that the contact angles undergo two transitions upon changing the substrate from rigid to soft. The microscopic wetting angles deviate from Young’s law when
$\gamma /E$. We show that the contact angles undergo two transitions upon changing the substrate from rigid to soft. The microscopic wetting angles deviate from Young’s law when 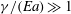 $\gamma /(Ea)\gg 1$, while the apparent macroscopic angle only changes in the very soft limit
$\gamma /(Ea)\gg 1$, while the apparent macroscopic angle only changes in the very soft limit 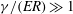 $\gamma /(ER)\gg 1$. The elastic deformations are worked out for the simplifying case where the solid surface energy is assumed to be constant. The total free energy turns out to be lower on softer substrates, consistent with recent experiments.
$\gamma /(ER)\gg 1$. The elastic deformations are worked out for the simplifying case where the solid surface energy is assumed to be constant. The total free energy turns out to be lower on softer substrates, consistent with recent experiments.