Hostname: page-component-669899f699-cf6xr Total loading time: 0 Render date: 2025-04-27T05:16:11.868Z Has data issue: false hasContentIssue false
  • English
  • Français

Droplet impact on a superhydrophobic solid substrate with a superhydrophilic annulus

Published online by Cambridge University Press:  02 October 2024

Ziqiang Ma Open the ORCID record for Ziqiang Ma [Opens in a new window] ,
Wanqiu Zhang Open the ORCID record for Wanqiu Zhang [Opens in a new window] ,
Qi Zhang Open the ORCID record for Qi Zhang [Opens in a new window]  and
Xinping Zhou Open the ORCID record for Xinping Zhou [Opens in a new window]
Ziqiang Ma
Affiliation:
School of Mechanical Science and Engineering, Huazhong University of Science and Technology, Wuhan 430074, PR China
Wanqiu Zhang
Affiliation:
School of Mechanical Science and Engineering, Huazhong University of Science and Technology, Wuhan 430074, PR China
Qi Zhang
Affiliation:
School of Mechanical Science and Engineering, Huazhong University of Science and Technology, Wuhan 430074, PR China
Xinping Zhou*
Affiliation:
School of Mechanical Science and Engineering, Huazhong University of Science and Technology, Wuhan 430074, PR China State Key Laboratory of Intelligent Manufacturing Equipment and Technology, Huazhong University of Science and Technology, Wuhan 430074, PR China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

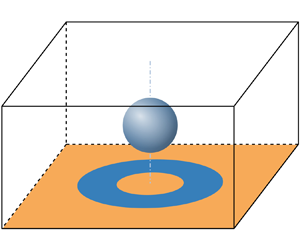
Direct numerical simulations of the droplet impact on a flat solid surface with an annular part are conducted. We investigate droplet impact on a superhydrophobic substrate with a superhydrophilic annulus to understand the formation conditions of droplets in different states. The location and size of superhydrophilic annulus are carried out through the phase diagram. We describe the formation process of droplets in three different states and the spreading radius with time to catch the rupture time of the film. Two different ruptures occur in the spreading stage or the retraction stage, respectively. The rupture times from these two mechanisms observed numerically are found to be a key factor resulting in partial rebound and lens-shaped/ring-shaped droplets. Finally, the influence of non-dimensional numbers on the formation of the ring-shaped droplet is demonstrated. The Weber number can alter the amplitude of the up and down oscillation on the droplet's upper surface, while the Froude number affects primarily the time to form the central penetrating hole. This gives the guidance and method to control the ring-shaped droplets formation time.

JFM classification

Drops and Bubbles: Drops
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 996 , 10 October 2024 , A20
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Afkhami, S., Buongiorno, J., Guion, A., Popinet, S., Saade, Y., Scardovelli, R. & Zaleski, S. 2018 Transition in a numerical model of contact line dynamics and forced dewetting. J. Comput. Phys. 374, 1061–1093.CrossRefGoogle Scholar
Afkhami, S., Zaleski, S. & Bussmann, M. 2009 A mesh-dependent model for applying dynamic contact angles to VOF simulations. J. Comput. Phys. 228 (15), 5370–5389.CrossRefGoogle Scholar
Bartolo, D., Josserand, C. & Bonn, D. 2005 Retraction dynamics of aqueous drops upon impact on non-wetting surfaces. J. Fluid Mech. 545, 329–338.CrossRefGoogle Scholar
Bartolo, D., Josserand, C. & Bonn, D. 2006 Singular jets and bubbles in drop impact. Phys. Rev. Lett. 96 (12), 124501.CrossRefGoogle ScholarPubMed
Bird, J.C., Dhiman, R., Kwon, H.M. & Varanasi, K.K. 2013 Reducing the contact time of a bouncing drop. Nature 503 (7476), 385–388.CrossRefGoogle ScholarPubMed
Bird, J.C., Mandre, S. & Stone, H.A. 2008 Short-time dynamics of partial wetting. Phys. Rev. Lett. 100 (23), 234501.CrossRefGoogle ScholarPubMed
Cheng, X., Sun, T.P. & Gordillo, L. 2022 Drop impact dynamics: impact force and stress distributions. Annu. Rev. Fluid Mech. 54 (1), 57–81.CrossRefGoogle Scholar
Chubynsky, M.V., Belousov, K.I., Lockerby, D.A. & Sprittles, J.E. 2020 Bouncing off the walls: the influence of gas-kinetic and van der Waals effects in drop impact. Phys. Rev. Lett. 124 (8), 084501.CrossRefGoogle Scholar
Eggers, J., Fontelos, M.A., Josserand, C. & Zaleski, S. 2010 Drop dynamics after impact on a solid wall: theory and simulations. Phys. Fluids 22 (6), 062101.CrossRefGoogle Scholar
Girard, H.L., Soto, D. & Varanasi, K.K. 2019 Waterbowls: reducing impacting droplet interactions by momentum redirection. ACS Nano 13 (7), 7729–7735.CrossRefGoogle ScholarPubMed
Hicks, P.D. & Purvis, R. 2010 Air cushioning and bubble entrapment in three-dimensional droplet impacts. J. Fluid Mech. 649, 135–163.CrossRefGoogle Scholar
Jian, Z., Josserand, C., Popinet, S., Ray, P. & Zaleski, S. 2018 Two mechanisms of droplet splashing on a solid substrate. J. Fluid Mech. 835, 1065–1086.CrossRefGoogle Scholar
Josserand, C. & Thoroddsen, S.T. 2016 Drop impact on a solid surface. Annu. Rev. Fluid Mech. 48 (1), 365–391.CrossRefGoogle Scholar
Kim, S., Moon, M.W. & Kim, H.Y. 2013 Drop impact on super-wettability-contrast annular patterns. J. Fluid Mech. 730, 328–342.CrossRefGoogle Scholar
Kim, S., Moon, M.W. & Kim, H.Y. 2021 Liquid spreading along nanostructured superhydrophilic lanes. Phys. Rev. Fluids 6 (3), 034002.CrossRefGoogle Scholar
Korobkin, A.A., Ellis, A.S. & Smith, F.T. 2008 Trapping of air in impact between a body and shallow water. J. Fluid Mech. 611, 365–394.CrossRefGoogle Scholar
Lagubeau, G., Fontelos, M.A., Josserand, C., Maurel, A., Pagneux, V. & Petitjeans, P. 2012 Spreading dynamics of drop impacts. J. Fluid Mech. 713, 50–60.CrossRefGoogle Scholar
Langley, K., Li, E.Q. & Thoroddsen, S.T. 2017 Impact of ultra-viscous drops: air-film gliding and extreme wetting. J. Fluid Mech. 813, 647–666.CrossRefGoogle Scholar
Li, E.Q. & Thoroddsen, S.T. 2015 Time-resolved imaging of a compressible air disc under a drop impacting on a solid surface. J. Fluid Mech. 780, 636–648.CrossRefGoogle Scholar
Li, H., Fang, W., Li, Y., Yang, Q., Li, M., Li, Q., Feng, X.Q. & Song, Y. 2019 Spontaneous droplets gyrating via asymmetric self-splitting on heterogeneous surfaces. Nat. Commun. 10 (1), 950.CrossRefGoogle ScholarPubMed
Lin, C., Cao, D., Zhao, D., Wei, P., Chen, S. & Liu, Y. 2022 Dynamics of droplet impact on a ring surface. Phys. Fluids 34 (1), 012004.CrossRefGoogle Scholar
Liu, Y., Moevius, L., Xu, X., Qian, T., Yeomans, J.M. & Wang, Z. 2014 Pancake bouncing on superhydrophobic surfaces. Nat. Phys. 10 (7), 515–519.CrossRefGoogle ScholarPubMed
Mandre, S., Mani, M. & Brenner, M.P. 2009 Precursors to splashing of liquid droplets on a solid surface. Phys. Rev. Lett. 102 (13), 134502.CrossRefGoogle ScholarPubMed
Mani, M., Mandre, S. & Brenner, M.P. 2010 Events before droplet splashing on a solid surface. J. Fluid Mech. 647, 163–185.CrossRefGoogle Scholar
Pack, M., Hu, H., Kim, D., Zheng, Z., Stone, H. & Sun, Y. 2017 Failure mechanisms of air entrainment in drop impact on lubricated surfaces. Soft Matt. 13 (12), 2402–2409.CrossRefGoogle ScholarPubMed
Popinet, S. 2003 Gerris: a tree-based adaptive solver for the incompressible Euler equations in complex geometries. J. Comput. Phys. 190 (2), 572–600.CrossRefGoogle Scholar
Popinet, S. 2009 An accurate adaptive solver for surface-tension-driven interfacial flows. J. Comput. Phys. 228 (16), 5838–5866.CrossRefGoogle Scholar
Popinet, S. 2018 Numerical models of surface tension. Annu. Rev. Fluid Mech. 50 (1), 49–75.CrossRefGoogle Scholar
Riboux, G. & Gordillo, J.M. 2014 Experiments of drops impacting a smooth solid surface: a model of the critical impact speed for drop splashing. Phys. Rev. Lett. 113 (2), 024507.CrossRefGoogle Scholar
Richard, D., Clanet, C. & Quéré, D. 2002 Contact time of a bouncing drop. Nature 417 (6891), 811.CrossRefGoogle ScholarPubMed
Richard, D. & Quéré, D. 2000 Bouncing water drops. Europhys. Lett. 50 (6), 769.CrossRefGoogle Scholar
Rioboo, R., Tropea, C. & Marengo, M. 2001 Outcomes from a drop impact on solid surfaces. Atomiz. Sprays 11 (2), 155–165.CrossRefGoogle Scholar
Roisman, I.V. 2009 Inertia dominated drop collisions. II. An analytical solution of the Navier–Stokes equations for a spreading viscous film. Phys. Fluids 21 (5), 052104.CrossRefGoogle Scholar
de Ruiter, J., van den Ende, D. & Mugele, F. 2015 a Air cushioning in droplet impact. II. Experimental characterization of the air film evolution. Phys. Fluids 27 (1), 012105.CrossRefGoogle Scholar
de Ruiter, J., Lagraauw, R., van den Ende, D. & Mugele, F. 2015 b Wettability-independent bouncing on flat surfaces mediated by thin air films. Nat. Phys. 11 (1), 48–53.CrossRefGoogle Scholar
Russo, A., Icardi, M., Elsharkawy, M., Ceglia, D., Asinari, P. & Megaridis, C.M. 2020 Numerical simulation of droplet impact on wettability-patterned surfaces. Phys. Rev. Fluids 5 (7), 074002.CrossRefGoogle Scholar
Schutzius, T.M., Graeber, G., Elsharkawy, M., Oreluk, J. & Megaridis, C.M. 2014 Morphing and vectoring impacting droplets by means of wettability-engineered surfaces. Sci. Rep. 4 (1), 7029.CrossRefGoogle ScholarPubMed
Sharma, P.K. & Dixit, H.N. 2021 Regimes of wettability-dependent and wettability-independent bouncing of a drop on a solid surface. J. Fluid Mech. 908, A37.CrossRefGoogle Scholar
Smith, F.T., Li, L. & Wu, G.X. 2003 Air cushioning with a lubrication/inviscid balance. J. Fluid Mech. 482, 291–318.CrossRefGoogle Scholar
Song, D., Song, B., Hu, H., Du, X. & Zhou, F. 2015 Selectively splitting a droplet using superhydrophobic stripes on hydrophilic surfaces. Phys. Chem. Chem. Phys. 17 (21), 13800–13803.CrossRefGoogle ScholarPubMed
Thoroddsen, S.T., Etoh, T.G. & Takehara, K. 2008 High-speed imaging of drops and bubbles. Annu. Rev. Fluid Mech. 40 (1), 257–285.CrossRefGoogle Scholar
Thoroddsen, S.T., Etoh, T.G., Takehara, K., Ootsuka, N. & Hatsuki, Y. 2005 The air bubble entrapped under a drop impacting on a solid surface. J. Fluid Mech. 545, 203–212.CrossRefGoogle Scholar
Tian, Y., Liu, Y., Peng, Z., Xu, C., Ye, D., Guan, Y., Zhou, X., Deng, W. & Huang, Y. 2022 a Air entrapment of a neutral drop impacting onto a flat solid surface in electric fields. J. Fluid Mech. 946, A21.CrossRefGoogle Scholar
Tian, Y., Peng, Z., Liu, Y., Di, L., Zhan, Z., Ye, D., Guan, Y., Zhou, X., Deng, W. & Huang, Y. 2022 b Effects of the electric field on the overall drop impact on a solid surface. Phys. Rev. Fluids 7 (11), 113604.CrossRefGoogle Scholar
Tian, Y., Wang, H., Zhou, X., Xie, Z., Zhu, X., Chen, R., Ding, Y. & Liao, Q. 2022 c How does the electric field make a droplet exhibit the ejection and rebound behaviour on a superhydrophobic surface? J. Fluid Mech. 941, A18.CrossRefGoogle Scholar
Wang, D., Jiang, Y., Zhu, Z., Yin, W., Asawa, K., Choi, C.H. & Drelich, J.W. 2020 Contact line and adhesion force of droplets on concentric ring-textured hydrophobic surfaces. Langmuir 36 (10), 2622–2628.CrossRefGoogle ScholarPubMed
Wang, X., Sun, D.L., Wang, X.D. & Yan, W.M. 2019 Dynamics of droplets impacting hydrophilic surfaces decorated with a hydrophobic strip. Intl J. Heat Mass Transfer 135, 235–246.CrossRefGoogle Scholar
Wildeman, S., Visser, C.W., Sun, C. & Lohse, D. 2016 On the spreading of impacting drops. J. Fluid Mech. 805, 636–655.CrossRefGoogle Scholar
Xu, J., Chen, Y. & Xie, J. 2018 Non-dimensional numerical study of droplet impacting on heterogeneous hydrophilicity/hydrophobicity surface. Intl J. Heat Mass Transfer 116, 951–968.CrossRefGoogle Scholar
Yarin, A. 2006 Drop impact dynamics: splashing, spreading, receding, bouncing. Annu. Rev. Fluid Mech. 38 (1), 159–192.CrossRefGoogle Scholar
Zhang, T., Wu, J. & Lin, X. 2022 Lateral motion of a solid with a heterogeneous wettability surface driven by impacting droplets. J. Fluid Mech. 946, A31.CrossRefGoogle Scholar
Zhao, Z., Li, H., Hu, X., Li, A., Cai, Z., Huang, Z., Su, M., Li, F., Li, M. & Song, Y. 2019 Steerable droplet bouncing for precise materials transportation. Adv. Mater. Interfaces 6 (21), 1901033.CrossRefGoogle Scholar
Zhao, Z., Li, H., Li, A., Fang, W., Cai, Z., Li, M., Feng, X. & Song, Y. 2021 Breaking the symmetry to suppress the Plateau–Rayleigh instability and optimize hydropower utilization. Nat. Commun. 12 (1), 6899.CrossRefGoogle ScholarPubMed