Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-17T13:21:08.389Z Has data issue: false hasContentIssue false
  • English
  • Français

Droplet deformation and heat transfer in isotropic turbulence

Published online by Cambridge University Press:  05 May 2017

Daniel L. Albernaz Open the ORCID record for Daniel L. Albernaz [Opens in a new window] ,
M. Do-Quang ,
J. C. Hermanson  and
G. Amberg
Daniel L. Albernaz*
Affiliation:
Department of Mechanics, Linné Flow Center, The Royal Institute of Technology, 100 44 Stockholm, Sweden
M. Do-Quang
Affiliation:
Department of Mechanics, Linné Flow Center, The Royal Institute of Technology, 100 44 Stockholm, Sweden
J. C. Hermanson
Affiliation:
Department of Aeronautics and Astronautics, University of Washington, Seattle, WA 98195, USA
G. Amberg
Affiliation:
Department of Mechanics, Linné Flow Center, The Royal Institute of Technology, 100 44 Stockholm, Sweden
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The heat and mass transfer of deformable droplets in turbulent flows is crucial to a wide range of applications, such as cloud dynamics and internal combustion engines. This study investigates a single droplet undergoing phase change in isotropic turbulence using numerical simulations with a hybrid lattice Boltzmann scheme. Phase separation is controlled by a non-ideal equation of state and density contrast is taken into consideration. Droplet deformation is caused by pressure and shear stress at the droplet interface. The statistics of thermodynamic variables are quantified and averaged over both the liquid and vapour phases. The occurrence of evaporation and condensation is correlated to temperature fluctuations, surface tension variation and turbulence intensity. The temporal spectra of droplet deformations are analysed and related to the droplet surface area. 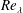Different modes of oscillation are clearly identified from the deformation power spectrum for low Taylor Reynolds number $Re_{\unicode[STIX]{x1D706}}$, whereas nonlinearities are produced with the increase of 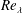$Re_{\unicode[STIX]{x1D706}}$, as intermediate frequencies are seen to overlap. As an outcome, a continuous spectrum is observed, which shows a decrease in the power spectrum that scales as ${\sim}f^{-3}$. Correlations between the droplet Weber number, deformation parameter, fluctuations of the droplet volume and thermodynamic variables are also developed.

JFM classification

Phase change: Condensation/evaporation Drops and Bubbles: Drops Turbulent Flows: Isotropic turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 820 , 10 June 2017 , pp. 61 - 85
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Albernaz, D. L., Amberg, G. & Do-Quang, M. 2016 Simulation of a suspended droplet under evaporation with Marangoni effects. Intl J. Heat Mass Transfer 97, 853–860.CrossRefGoogle Scholar
Albernaz, D. L., Do-Quang, M. & Amberg, G. 2015 Multirelaxation-time lattice Boltzmann model for droplet heating and evaporation under forced convection. Phys. Rev. E 91, 043012.Google ScholarPubMed
Albernaz, D. L., Do-Quang, M., Hermanson, J. C. & Amberg, G. 2016 Thermodynamics of a real fluid near the critical point in numerical simulations of isotropic turbulence. Phys. Fluids 28, 125105.CrossRefGoogle Scholar
Balaji, B. R., Ramamurthi, V. & Gogos, K. G. 2011 A numerical study of evaporation characteristics of spherical n-dodecane droplets in high pressure nitrogen environment. Phys. Fluids 23, 063601.CrossRefGoogle Scholar
Biferale, L., Meneveau, C. & Verzicco, R. 2014 Deformation statistics of sub-Kolmogorov-scale ellipsoidal neutrally buoyant drops in isotropic turbulence. J. Fluid Mech. 754, 184–207.CrossRefGoogle Scholar
Bird, R. B. 1960 Transport Phenomena. Wiley.Google Scholar
Connington, K. & Lee, T. 2012 A review of spurious currents in the lattice Boltzmann method for multiphase flows. J. Mech. Sci. Technol. 26, 3857–3863.CrossRefGoogle Scholar
Donzis, D. A. & Jagannathan, S. 2013 Fluctuations of thermodynamic variables in stationary compressible turbulence. J. Fluid Mech. 733, 221–244.CrossRefGoogle Scholar
Hinze, O. 1955 Fundamentals of the hydrodynamic mechanism of splitting in dispersion processes. AIChE J. 1, 289–295.CrossRefGoogle Scholar
Huang, R. & Wu, H. 2014 A modified multiple-relaxation-time lattice Boltzmann model for convection–diffusion equation. J. Comput. Phys. 274, 50–63.CrossRefGoogle Scholar
d’Humieres, D., Ginzburg, I., Krafczyk, M., Lallemand, P. & Luo, L. S. 2002 Multiple-relaxation-time lattice Boltzmann models in three-dimensions. Proc. R. Soc. Lond. A 360, 437–451.Google ScholarPubMed
Ishihara, T., Gotoh, T. & Kaneda, Y. 2009 Study of high-Reynolds number isotropic turbulence by direct numerical simulation. Annu. Rev. Fluid Mech. 41, 165–180.CrossRefGoogle Scholar
Kareem, W. A., Izawa, S., Xiong, A.-K. & Fukunishi, Y. 2009 Lattice Boltzmann simulations of homogeneous isotropic turbulence. Comput. Maths Applics 58, 1055–1061.CrossRefGoogle Scholar
Kolmogorov, A. N. 1941 The local structure of turbulence in an incompressible fluid with very large Reynolds number. C. R. Acad. Sci. Paris 30, 301.Google Scholar
Kupershtokh, A. L. & Medvedev, D. A. 2006 Lattice Boltzmann equation method in electrohydrodynamic problems. J. Electrostat. 64, 581–585.CrossRefGoogle Scholar
Kupershtokh, A. L., Medvedev, D. A. & Karpov, D. I. 2009 On equations of state in a lattice Boltzmann method. Comput. Maths Applics. 58, 965–974.CrossRefGoogle Scholar
Lallemand, P. & Luo, L. S. 2000 Theory of the lattice Boltzmann method: dispersion, dissipation, isotropy, galilean invariance, and stability. Phys. Rev. E 61, 6546.Google ScholarPubMed
Lallemand, P. & Luo, L. S. 2003a Theory of the lattice Boltzmann method: acoustic and thermal properties in two and three dimensions. Phys. Rev. E 68, 036706.Google ScholarPubMed
Lallemand, P. & Luo, L. S. 2003b Hybrid finite-difference thermal lattice Boltzmann equation. Intl J. Mod. Phys. B 17, 41.CrossRefGoogle Scholar
Lasheras, J. C., Eastwood, A., Martínez-Bazán, C. & Montañés, J. L. 2002 A review of statistical models for the break-up of an immiscible fluid immersed into a fully developed turbulent flow. Intl J. Multiphase Flow 28, 247–278.CrossRefGoogle Scholar
Lefebvre, A. H. 1989 Atomization and Sprays. Taylor & Francis.Google Scholar
Lemmon, E. W., McLinden, M. O. & Friend, D.G. 2013 Thermophysical properties of fluid systems. In NIST Chemistry WebBook, NIST Standard Reference Database Number (ed. Linstrom, P. J. & Mallard, W. G.), vol. 69. National Institute of Standards and Technology.Google Scholar
Li, Q., Luo, K. H., Kang, Q. J., He, Y. L., Chen, Q. & Liu, Q. 2016 Lattice Boltzmann methods for multiphase flow and phase-change heat transfer. Prog. Energy Combust. Sci. 52, 62–105.CrossRefGoogle Scholar
Li, Q., Luo, K. H. & Li, X. J. 2012 Forcing scheme in pseudopotential lattice Boltzmann model for multiphase flows. Phys. Rev. E 86, 016709.Google ScholarPubMed
Lord Rayleigh 1879 On the capillary phenomena of jets. Proc. R. Soc. Lond. 29, 71–97.CrossRefGoogle Scholar
Lorensen, W. E. & Cline, H. E. 1987 Marching cubes: a high resolution 3D surface construction algorithm. Comput. Graph. 21, 163–169.CrossRefGoogle Scholar
Márkus, A. & Házi, G. 2011 Simulation of evaporation by an extension of the pseudopotential lattice Boltzmann method: a quantitative analysis. Phys. Rev. E 83, 046705.Google ScholarPubMed
McNamara, G. R. 1995 Stabilization of thermal lattice Boltzmann models. Phys. Rev. E 81, 395–408.Google Scholar
Perlekar, P., Biferale, L., Sbragaglia, M., Srivstava, S. & Toschi, F. 2012 Droplet size distribution in homogeneous isotropic turbulence. Phys. Fluids 24, 065101.CrossRefGoogle Scholar
Petersen, M. R. & Livescu, D. 2010 Forcing for statistically stationary compressible isotropic turbulence. Phys. Fluids 22, 116101.CrossRefGoogle Scholar
Qian, D., McLaughlin, J. B., Sankaranarayanan, K., Sundaresan, S. & Kontomaris, K. 2006 Simulation of bubble breakup dynamics in homogeneous turbulence. Chem. Engng Commun. 193, 1038–1063.CrossRefGoogle Scholar
Risso, F. & Fabre, J. 1998 Oscillations and breakup of a bubble immersed in a turbulent field. J. Fluid Mech. 372, 323–355.CrossRefGoogle Scholar
Safari, H., Rahimian, M. H. & Krafczyk, M. 2013 Extended lattice Boltzmann method for numerical simulation of thermal phase change in two-phase fluid flow. Phys. Rev. E 88, 013304.Google ScholarPubMed
Safari, H., Rahimian, M. H. & Krafczyk, M. 2014 Consistent simulation of droplet evaporation based on the phase-field multiphase lattice Boltzmann method. Phys. Rev. E 90, 033305.Google ScholarPubMed
Sbragaglia, M., Benzi, R., Biferale, L., Succi, S., Sugiyama, K. & Toschi, F. 2007 Generalized lattice Boltzmann method with multirange pseudopotential. Phys. Rev. E 75, 026702.Google ScholarPubMed
Scarbolo, L. & Soldati, A. 2013 Turbulence modulation across the interface of a large deformable drop. J. Turbul. 14, 27–43.CrossRefGoogle Scholar
Scarbolo, L. & Soldati, A. 2015 Wall drag modification by large deformable droplets in turbulent channel flow. Comput. Fluids 113, 87–92.CrossRefGoogle Scholar
Skartlien, R., Sollum, E. & Schumann, H. 2013 Droplet size distributions in turbulent emulsions: breakup criteria and surfactant effects from direct numerical simulations. J. Chem. Phys. 139, 174901.Google ScholarPubMed
Thomson, W. 1871 On the equilibrium of vapour at a curved surface of liquid. Phil. Mag. 42, 448–452.CrossRefGoogle Scholar
Thomson, W. 2009 Lagrangian properties of particles in turbulence. Annu. Rev. Fluid Mech. 41, 375.Google Scholar
Treeck, C., Rank, E., Krafczyk, M., Toelke, J. & Nachtwey, B. 2006 Extension of a hybrid thermal LBE scheme for large-eddy simulations of turbulent convective flows. Comput. Fluids 35, 863–871.CrossRefGoogle Scholar
Verhaeghe, F., Blanpain, B. & Wollants, P. 2007 Lattice Boltzmann method for double-diffuse natural convection. Phys. Rev. E 75, 046705.Google Scholar
Wagner, A. J. 2006 Thermodynamic consistency of liquid–gas lattice Boltzmann simulations. Phys. Rev. E 74, 056703.Google ScholarPubMed
Walter, J. F. & Blanch, H. W. 1986 Bubble break-up in gas–liquid bioreactors: break-up in turbulent flows. Chem. Engng J. 32, 7–17.CrossRefGoogle Scholar