Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Longmire, Ellen K.
and
Bordoloi, Ankur D.
2015.
Drop Penetration through a Constriction: Effect of Surrounding Fluid.
Procedia IUTAM,
Vol. 15,
Issue. ,
p.
194.
Zhu, Pingan
Kong, Tiantian
Lei, Leyan
Tian, Xiaowei
Kang, Zhanxiao
and
Wang, Liqiu
2016.
Droplet Breakup in Expansion-contraction Microchannels.
Scientific Reports,
Vol. 6,
Issue. 1,
Xu, Jinliang
Xie, Jian
He, Xiaotian
Cheng, Yu
and
Liu, Qi
2017.
Water drop impacts on a single-layer of mesh screen membrane: Effect of water hammer pressure and advancing contact angles.
Experimental Thermal and Fluid Science,
Vol. 82,
Issue. ,
p.
83.
Zinchenko, Alexander Z.
and
Davis, Robert H.
2017.
Motion of Deformable Drops Through Porous Media.
Annual Review of Fluid Mechanics,
Vol. 49,
Issue. 1,
p.
71.
Bordoloi, Ankur D.
and
Longmire, Ellen K.
2018.
Local velocity variations for a drop moving through an orifice: Effects of edge geometry and surface wettability.
Physical Review Fluids,
Vol. 3,
Issue. 12,
Zhang, Gannian
Quetzeri-Santiago, Miguel A.
Stone, Corinne A.
Botto, Lorenzo
and
Castrejón-Pita, J. Rafael
2018.
Droplet impact dynamics on textiles.
Soft Matter,
Vol. 14,
Issue. 40,
p.
8182.
Yuan, Xiaolei
Chai, Zhenhua
and
Shi, Baochang
2019.
Dynamic behavior of droplet through a confining orifice:A lattice Boltzmann study.
Computers & Mathematics with Applications,
Vol. 77,
Issue. 10,
p.
2640.
Sen, Uddalok
Roy, Tamal
Chatterjee, Souvick
Ganguly, Ranjan
and
Megaridis, Constantine M.
2019.
Post-Impact Behavior of a Droplet Impacting on a Permeable Metal Mesh with a Sharp Wettability Step.
Langmuir,
Vol. 35,
Issue. 39,
p.
12711.
Gissinger, Jacob R.
Zinchenko, Alexander Z.
and
Davis, Robert H.
2019.
Drops with insoluble surfactant squeezing through interparticle constrictions.
Journal of Fluid Mechanics,
Vol. 878,
Issue. ,
p.
324.
Liu, Zhongyi
Li, Siqi
Fang, Haisheng
and
Pan, Xiaolong
2020.
Four Modes of Droplet Permeation Through a Micro-pore with a T-Shaped Junction During Spreading.
Transport in Porous Media,
Vol. 132,
Issue. 1,
p.
219.
Chen, Hao
Nie, Qichun
and
Fang, Haisheng
2020.
Dynamic behavior of droplets on confined porous substrates: A many-body dissipative particle dynamics study.
Physics of Fluids,
Vol. 32,
Issue. 10,
Gissinger, Jacob R.
Zinchenko, Alexander Z.
and
Davis, Robert H.
2021.
Drop squeezing between arbitrary smooth obstacles.
Journal of Fluid Mechanics,
Vol. 908,
Issue. ,
Singla, Aditya
and
Ray, Bahni
2021.
Effects of surface topography on low Reynolds number droplet/bubble flow through a constricted passage.
Physics of Fluids,
Vol. 33,
Issue. 1,
Gao, Ming
Liang, Jia
Chen, Lu
Wang, Dongmin
and
Wang, Zhiyun
2022.
Lattice Boltzmann simulation of droplet impact on orifice plate with different wettability.
Computers & Fluids,
Vol. 248,
Issue. ,
p.
105674.
Zhang, Ang
Su, Dongbo
Li, Chuangming
Gao, Yuyang
Dong, Zhihua
Bai, Shengwen
Jiang, Bin
and
Pan, Fusheng
2022.
Three-dimensional phase-field lattice-Boltzmann simulations of a rising bubble interacting with obstacles: Shape quantification and parameter dependence.
Physics of Fluids,
Vol. 34,
Issue. 10,
Nashwan, M. G.
Ragab, Kareem E.
and
Faltas, M. S.
2022.
Axisymmetric slow motion of a non-deformable spherical droplet or slip particle toward an orifice in a plane wall.
Physics of Fluids,
Vol. 34,
Issue. 8,
Lombardi, Valentina
La Rocca, Michele
Montessori, Andrea
Succi, Sauro
and
Prestininzi, Pietro
2022.
On the fate of a drop jumping over a gap.
Journal of Fluid Mechanics,
Vol. 949,
Issue. ,
Wang, Ya-Ping
Zhou, Jin-Xiang
Li, Jia-Qing
Khan, Adnan
Niu, Xiao-Dong
Chen, Mu-Feng
and
Yang, Liming
2023.
Magnetic field-enhanced orifice traversal of droplets: Minimizing surface adhesion for improved efficiency.
Physics of Fluids,
Vol. 35,
Issue. 12,
Catsoulis, Sotiris
Sen, Uddalok
Walther, Jens H.
and
Megaridis, Constantine M.
2023.
Droplet impact on a wettability‐patterned woven mesh.
Droplet,
Vol. 2,
Issue. 3,
Singla, Aditya
Mehul, Bakhshi
and
Ray, Bahni
2024.
Droplet dynamics in a constricted microchannel.
Chemical Engineering Science,
Vol. 300,
Issue. ,
p.
120532.
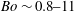 $\mathit{Bo}\sim 0.8{-}11$) through a circular confining orifice (ratio of orifice diameter to drop diameter,
$\mathit{Bo}\sim 0.8{-}11$) through a circular confining orifice (ratio of orifice diameter to drop diameter, 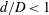 $d/D<1$) was studied using high-speed imaging. Drops of water/glycerin, surrounded by silicone oil, fall toward and encounter the orifice plate after reaching terminal speed. The effects of surface wettability were investigated for both round-edged and sharp-edged orifices. For the round-edged case, a thin film of surrounding oil prevents the drop fluid from contacting the orifice surface, such that the flow outcomes of the drops are independent of surface wettability. For
$d/D<1$) was studied using high-speed imaging. Drops of water/glycerin, surrounded by silicone oil, fall toward and encounter the orifice plate after reaching terminal speed. The effects of surface wettability were investigated for both round-edged and sharp-edged orifices. For the round-edged case, a thin film of surrounding oil prevents the drop fluid from contacting the orifice surface, such that the flow outcomes of the drops are independent of surface wettability. For 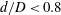 $d/D<0.8$, the boundary between drop capture and release depends on a modified Bond number relating drop gravitational time scale to orifice surface tension time scale and is independent of viscosity ratio. Drops that release break into multiple fragments for larger
$d/D<0.8$, the boundary between drop capture and release depends on a modified Bond number relating drop gravitational time scale to orifice surface tension time scale and is independent of viscosity ratio. Drops that release break into multiple fragments for larger 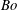 $\mathit{Bo}$ and smaller
$\mathit{Bo}$ and smaller 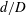 $d/D$. For the sharp-edged case, a contact is initiated at the orifice edge immediately upon impact, such that surface wettability influences the drop outcome. When the surface is hydrophobic, the contact line motion through the orifice enhances penetration of the drop fluid, but the trailing interface becomes pinned at the orifice edge, inhibiting drop release. When the surface is hydrophilic, a fraction of the drop fluid is always captured because the drop fluid spreads on both the upper and lower plate surfaces.
$d/D$. For the sharp-edged case, a contact is initiated at the orifice edge immediately upon impact, such that surface wettability influences the drop outcome. When the surface is hydrophobic, the contact line motion through the orifice enhances penetration of the drop fluid, but the trailing interface becomes pinned at the orifice edge, inhibiting drop release. When the surface is hydrophilic, a fraction of the drop fluid is always captured because the drop fluid spreads on both the upper and lower plate surfaces.


