Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Aguiar, Joao
Birch, David M.
and
Pelacci, Manuel
2018.
Wake vortex mechanisms behind semi-porous cylinders.
Hasheminejad, Seyyed M.
Rabiee, Amir H.
and
Bahrami, H. R. T.
2018.
Active closed-loop vortex-induced vibration control of an elastically mounted circular cylinder at low Reynolds number using feedback rotary oscillations.
Acta Mechanica,
Vol. 229,
Issue. 1,
p.
231.
Hasegawa, Mitsugu
and
Sakaue, Hirotaka
2018.
Microfiber Coating for Drag Reduction by Flocking Technology.
Coatings,
Vol. 8,
Issue. 12,
p.
464.
Gromke, Christof
and
Ruck, Bodo
2018.
On Wind Forces in the Forest-Edge Region During Extreme-Gust Passages and Their Implications for Damage Patterns.
Boundary-Layer Meteorology,
Vol. 168,
Issue. 2,
p.
269.
Xia, Chao
Wei, Zheng
Yuan, Haidong
Li, Qiliang
and
Yang, Zhigang
2018.
POD analysis of the wake behind a circular cylinder coated with porous media.
Journal of Visualization,
Vol. 21,
Issue. 6,
p.
965.
Gromke, Christof
2018.
Wind tunnel model of the forest and its Reynolds number sensitivity.
Journal of Wind Engineering and Industrial Aerodynamics,
Vol. 175,
Issue. ,
p.
53.
Arcondoulis, Elias
Ragni, Daniele
Rubio Carpio, Alejandro
Avallone, Francesco
Liu, Yu
Yang, Yannian
and
Li, Zhiyong
2019.
The internal and external flow fields of a structured porous coated cylinder and implications on flow-induced noise.
Arcondoulis, Elias J. G.
Liu, Yu
Li, Zhiyong
Yang, Yannian
and
Wang, Yong
2019.
Structured Porous Material Design for Passive Flow and Noise Control of Cylinders in Uniform Flow.
Materials,
Vol. 12,
Issue. 18,
p.
2905.
Hasegawa, Mitsugu
and
Sakaue, Hirotaka
2019.
Microfiber Coating for Flow Control over a Blunt Surface.
Coatings,
Vol. 9,
Issue. 10,
p.
664.
Geyer, Thomas F.
2020.
Vortex Shedding Noise from Finite, Wall-Mounted, Circular Cylinders Modified with Porous Material.
AIAA Journal,
Vol. 58,
Issue. 5,
p.
2014.
Bathla, Pranjal
and
Kennedy, John
2020.
3D Printed Structured Porous Treatments for Flow Control around a Circular Cylinder.
Fluids,
Vol. 5,
Issue. 3,
p.
136.
Arcondoulis, Elias
Liu, Yu
Geyer, Thomas F.
Sedaghatizadeh, Nima
and
Arjomandi, Maziar
2020.
Aeroacoustic performance of cylinders with a circumferential varying porous coating.
Geyer, Thomas F.
2020.
Experimental evaluation of cylinder vortex shedding noise reduction using porous material.
Experiments in Fluids,
Vol. 61,
Issue. 7,
Hu, Zhijie
Liu, Hanru
Chen, Nanshu
Hu, Jiawei
and
Tong, Fan
2020.
Vortex shedding noise and flow mode analysis of cylinder with full/partial porous coating.
Aerospace Science and Technology,
Vol. 106,
Issue. ,
p.
106154.
Zhang, Pikai
Liu, Yu
Li, Zhiyong
Liu, Hanru
and
Yang, Yannian
2020.
Numerical study on reducing aerodynamic drag and noise of circular cylinders with non-uniform porous coatings.
Aerospace Science and Technology,
Vol. 107,
Issue. ,
p.
106308.
Arcondoulis, Elias J. G.
Geyer, Thomas F.
and
Liu, Yu
2021.
An acoustic investigation of non-uniformly structured porous coated cylinders in uniform flow.
The Journal of the Acoustical Society of America,
Vol. 150,
Issue. 2,
p.
1231.
Yu, Haiyang
Xu, Zhihan
Chen, Wen-Li
Li, Hui
and
Gao, Donglai
2021.
Attenuation of vortex street by suction through the structured porous surface.
Physics of Fluids,
Vol. 33,
Issue. 12,
Wen, Kaibin
Arcondoulis, Elias J.G.
Li, Zhiyong
and
Liu, Yu
2021.
Structure resolved simulations of flow around porous coated cylinders based on a simplified pore-scale model.
Aerospace Science and Technology,
Vol. 119,
Issue. ,
p.
107181.
Arcondoulis, Elias J. G.
Geyer, Thomas F.
and
Liu, Yu
2021.
An investigation of wake flows produced by asymmetrically structured porous coated cylinders.
Physics of Fluids,
Vol. 33,
Issue. 3,
Guinness, Imogen
and
Persoons, Tim
2021.
Passive Flow Control for Drag Reduction on a Cylinder in Cross-Flow Using Leeward Partial Porous Coatings.
Fluids,
Vol. 6,
Issue. 8,
p.
289.
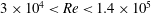 $3\times 10^{4}<Re<1.4\times 10^{5}$. The results show that a thin porous layer on the leeward side, either incorporated in the cylinder shape or applied on the cylinder surface, leads to an increase of base pressure on the leeward side of the cylinder. It causes a reduction of drag and dampens oscillation amplitudes when compared to a cylinder without coating. Results obtained for different configurations with varying key parameters (coating angles, layer thicknesses and pore sizes of the porous material) clearly indicate the drag-reducing and amplitude-damping potential of leeward coating. The amount of drag reduction and amplitude damping depends on the combination of key parameters. It was demonstrated that the lowered drag coefficients
$3\times 10^{4}<Re<1.4\times 10^{5}$. The results show that a thin porous layer on the leeward side, either incorporated in the cylinder shape or applied on the cylinder surface, leads to an increase of base pressure on the leeward side of the cylinder. It causes a reduction of drag and dampens oscillation amplitudes when compared to a cylinder without coating. Results obtained for different configurations with varying key parameters (coating angles, layer thicknesses and pore sizes of the porous material) clearly indicate the drag-reducing and amplitude-damping potential of leeward coating. The amount of drag reduction and amplitude damping depends on the combination of key parameters. It was demonstrated that the lowered drag coefficients 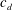 $c_{d}$ were almost constant in the tested range of Reynolds numbers. A maximum reduction of drag of 13.2 % was measured. In addition, the results revealed a strong reduction of the pressure fluctuations around cylinders with a leeward coating due to the shift of the vortex region further downstream.
$c_{d}$ were almost constant in the tested range of Reynolds numbers. A maximum reduction of drag of 13.2 % was measured. In addition, the results revealed a strong reduction of the pressure fluctuations around cylinders with a leeward coating due to the shift of the vortex region further downstream.