Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-05T01:06:32.217Z Has data issue: false hasContentIssue false
  • English
  • Français

Drag reduction in turbulent flows along a cylinder by streamwise-travelling waves of circumferential wall velocity

Published online by Cambridge University Press:  07 January 2019

Ming-Xiang Zhao Open the ORCID record for Ming-Xiang Zhao [Opens in a new window] ,
Wei-Xi Huang Open the ORCID record for Wei-Xi Huang [Opens in a new window]  and
Chun-Xiao Xu Open the ORCID record for Chun-Xiao Xu [Opens in a new window]
Ming-Xiang Zhao
Affiliation:
AML, Department of Engineering Mechanics, Tsinghua University, Beijing 100084, China
Wei-Xi Huang
Affiliation:
AML, Department of Engineering Mechanics, Tsinghua University, Beijing 100084, China
Chun-Xiao Xu*
Affiliation:
AML, Department of Engineering Mechanics, Tsinghua University, Beijing 100084, China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Drag reduction at the external surface of a cylinder in turbulent flows along the axial direction by circumferential wall motion is studied by direct numerical simulations. The circumferential wall oscillation can lead to drag reduction due to the formation of a Stokes layer, but it may also result in centrifugal instability, which can enhance turbulence and increase drag. In the present work, the Reynolds number based on the reference friction velocity and the nominal thickness of the boundary layer is 272. A map describing the relationship between the drag-reduction rate and the control parameters, namely, the angular frequency 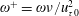$\unicode[STIX]{x1D714}^{+}=\unicode[STIX]{x1D714}\unicode[STIX]{x1D708}/u_{\unicode[STIX]{x1D70F}0}^{2}$ and the streamwise wavenumber 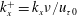$k_{x}^{+}=k_{x}\unicode[STIX]{x1D708}/u_{\unicode[STIX]{x1D70F}0}$, is obtained at the oscillation amplitude of 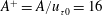${A^{+}=A/u}_{\unicode[STIX]{x1D70F}0}=16$, where 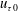$u_{\unicode[STIX]{x1D70F}0}$ is the friction velocity of the uncontrolled flow and $\unicode[STIX]{x1D708}$ is the kinematic viscosity of the fluid. The maximum drag-reduction rate and the maximum drag-increase rate are both approximately 48 %, which are respectively attained at 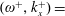$(\unicode[STIX]{x1D714}^{+},k_{x}^{+})=$ (0.0126, 0.0148) and (0.0246, 0.0018). The drag-reduction rate can be scaled well with the help of the effective thickness of the Stokes layer. The drag increase is observed in a narrow triangular region in the frequency–wavenumber plane. The vortices induced by the centrifugal instability become the primary coherent structure in the near-wall region, and they are closely correlated with the high skin friction. In these drag-increase cases, the effective control frequency or wavenumber is crucial in scaling the drag-increase rate. As the wall curvature normalised by the boundary layer thickness becomes larger, the drag-increase region in the 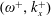$(\unicode[STIX]{x1D714}^{+},k_{x}^{+})$ plane as well as the maximum drag-increase rate also become larger. Net energy saving with a considerable drag-reduction rate is possible when reducing the oscillation amplitude. At 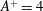$A^{+}=4$, a net energy saving of 18 % can be achieved with a drag-reduction rate of 25 % if only the power dissipation due to viscous stress is taken into account in an ideal actuation system.

JFM classification

Flow Control: Drag reduction Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulence control
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 862 , 10 March 2019 , pp. 75 - 98
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Auteri, F., Baron, A., Belan, M., Campanardi, G. & Quadrio, M. 2010 Experimental assessment of drag reduction by traveling waves in a turbulent pipe flow. Phys. Fluids 22 (11), 115103.Google Scholar
Baron, A. & Quadrio, M. 1996 Turbulent drag reduction by spanwise wall oscillations. Appl. Sci. Res. 55, 311–326.Google Scholar
Choi, K.-S. & Graham, M. 1998 Drag reduction of turbulent pipe flows by circular-wall oscillation. Phys. Fluids 10, 869538.Google Scholar
Choi, K.-S., Debisschop, J.-R. & Clayton, B. R. 1998 Turbulent boundary-layer control by means of spanwise-wall oscillation. AIAA J. 36 (7), 1157–1163.Google Scholar
Choi, J.-I., Xu, C.-X. & Sung, H. J. 2002 Drag reduction by spanwise wall oscillation in wall-bounded turbulent flows. AIAA J. 40 (5), 842–850.Google Scholar
Chung, S. Y., Rhee, G. H. & Sung, H. J. 2002 Direct numerical simulation of turbulent concentric annular pipe flow. Part 1. Flow field. Intl J. Heat Fluid Flow 23 (4), 426–440.Google Scholar
Gad-El Hak, M. 2000 Flow Control – Passive, Active and Reactive Flow Management. Cambridge University Press.Google Scholar
Gatti, D. & Quadrio, M. 2016 Reynolds-number dependence of turbulent skin-friction drag reduction induced by spanwise forcing. J. Fluid Mech. 802, 553–582.Google Scholar
Hunt, J. C. R., Wray, A. A. & Moin, P.1988 Eddies, stream, and convergence zones in turbulent flows. Center for Turbulence Research Report CTR-S88, p. 193.Google Scholar
Hurst, E., Yang, Q. & Chung, Y. M. 2014 The effect of Reynolds number on turbulent drag reduction by streamwise travelling waves. J. Fluid Mech. 759, 28–55.Google Scholar
Jung, W. J., Mangiavacchi, N. & Akhavan, R. 1992 Suppression of turbulence in wall-bounded flows by high-frequency spanwise oscillations. Phys. Fluids A 4 (8), 1605–1607.Google Scholar
Karniadakis, G. E., Israeli, M. & Orszag, S. A. 1991 High-order splitting methods for the incompressible Navier–Stokes equations. J. Comput. Phys. 97 (2), 414–443.Google Scholar
Kim, J. 2003 Control of turbulent boundary layers. Phys. Fluids 15 (5), 1093–1105.Google Scholar
Kim, J. 2011 Physics and control of wall turbulence for drag reduction. Phil. Trans. R. Soc. Lond. A 369, 1396–1411.Google Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.Google Scholar
Klewicki, J. C. 2010 Reynolds number dependence, scaling, and dynamics of turbulent boundary layers. Trans. ASME J. Fluids Engng 132 (9), 094001.Google Scholar
Kuwabara, S. & Takaki, R. 1975 Secondary flow around a circular cylinder in rotatory oscillation. J. Phys. Soc. Japan 38 (4), 1180–1186.Google Scholar
Ostilla-Mónico, R., Stevens, R. J. A. M., Grossmann, S., Verzicco, R. & Lohse, D. 2013 Optimal Taylor–Couette flow: direct numerical simulations. J. Fluid Mech. 719, 14–46.Google Scholar
Ostilla-Mónico, R., Van Der Poel, E. P., Verzicco, R., Grossmann, S. & Lohse, D. 2014 Exploring the phase diagram of fully turbulent Taylor–Couette flow. J. Fluid Mech. 761, 1–26.Google Scholar
Quadrio, M. 2011 Drag reduction in turbulent boundary layers by in-plane wall motion. Phil. Trans. R. Soc. Lond. A 369, 1428–1442.Google Scholar
Quadrio, M. & Ricco, P. 2004 Critical assessment of turbulent drag reduction through spanwise wall oscillation. J. Fluid Mech. 521, 251–271.Google Scholar
Quadrio, M. & Ricco, P. 2011 The laminar generalized Stokes layer and turbulent drag reduction. J. Fluid Mech. 667, 135–157.Google Scholar
Quadrio, M. & Sibilla, S. 2000 Numerical simulation of turbulent flow in a pipe oscillating around its axis. J. Fluid Mech. 424, 217–241.Google Scholar
Quadrio, M., Ricco, P. & Viotti, C. 2009 Streamwise-travelling waves of spanwise wall velocity for turbulent drag reduction. J. Fluid Mech. 627, 161–178.Google Scholar
Ricco, P. & Quadrio, M. 2008 Wall-oscillation conditions for drag reduction in turbulent channel flow. Intl J. Heat Fluid Flow 29, 601–612.Google Scholar
Skote, M. 2011 Turbulent boundary layer flow subject to streamwise oscillation of spanwise wall velocity. Phys. Fluids 23 (8), 081703.Google Scholar
Skote, M. 2012 Temporal and spatial transients in turbulent boundary layer flow over an oscillating wall. Intl J. Heat Fluid Flow 38, 1–12.Google Scholar
Skote, M. 2013 Comparison between spatial and temporal wall oscillations in turbulent boundary layer flows. J. Fluid Mech. 730, 273–294.Google Scholar
Skote, M. 2014 Scaling of the velocity profile in strongly drag reduced turbulent flows over and oscillation wall. Intl J. Heat Fluid Flow 50, 352–358.Google Scholar
Skote, M., Mishra, M. & Wu, Y. 2015 Drag reduction of a turbulent boundary layer over an oscillating wall and its variation with Reynolds number. Intl J. Aerosp. Engng 3, 1–9.Google Scholar
Taylor, G. I. 1923 Stability of a viscous liquid contained between two rotating cylinders. Phil. Trans. R. Soc. Lond. A 223, 289–343.Google Scholar
Touber, E. & Leschziner, M. A. 2012 Near-wall streak modification by spanwise oscillatory wall motion and drag-reduction mechanisms. J. Fluid Mech. 693, 150–200.Google Scholar
Viotti, C., Quadrio, M. & Luchini, P. 2009 Streamwise oscillation of spanwise velocity at the wall of a channel for turbulent drag reduction. Phys. Fluids 21, 115109.Google Scholar
Yudhistira, I. & Skote, M. 2011 Direct numerical simulation of a turbulent boundary layer over an oscillating wall. J. Turbul. 12, 1–17.Google Scholar