Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-26T08:28:15.467Z Has data issue: false hasContentIssue false
  • English
  • Français

Drag reduction in heated channels

Published online by Cambridge University Press:  23 January 2015

Daniel Floryan  and
J. M. Floryan
Daniel Floryan
Affiliation:
Department of Mechanical and Materials Engineering, The University of Western Ontario, London, Ontario, N6A 5B9, Canada
J. M. Floryan*
Affiliation:
Department of Mechanical and Materials Engineering, The University of Western Ontario, London, Ontario, N6A 5B9, Canada
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

It is known that the drag for flows driven by a pressure gradient in heated channels can be reduced below the level found in isothermal channels. This reduction occurs for spatially modulated heating and is associated with the formation of separation bubbles which isolate the main stream from direct contact with the solid wall. It is demonstrated that the use of a proper combination of spatially distributed and spatially uniform heating components results in an increase in the horizontal and vertical temperature gradients which lead to an intensification of convection which, in turn, significantly increases the drag reduction. An excessive increase of the uniform heating leads to breakup of the bubbles and the formation of complex secondary states, resulting in a deterioration of the system performance. This performance may, under certain conditions, still be better than that achieved using only spatially distributed heating. Detailed calculations have been carried out for the Prandtl number 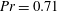$\mathit{Pr}=0.71$ and demonstrate that this technique is effective for flows with a Reynolds number 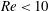$\mathit{Re}<10$; faster flows wash away separation bubbles. The question of net gain remains to be settled as it depends on the method used to achieve the desired wall temperature and on the cost of the required energy. The presented results provide a basis for the design of passive flow control techniques utilizing heating patterns as controlling agents.

JFM classification

Flow Control: Drag reduction Flow Control: Flow Control
Type
Papers
Information
Journal of Fluid Mechanics , Volume 765 , 25 February 2015 , pp. 353 - 395
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Present address: Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA.

References

Bergman, T. L., Lavine, A. S., Incropera, F. P. & Dewitt, D. P. 2011 Fundamentals of Heat and Mass Transfer, 7th edn. Wiley.Google Scholar
Bewley, T. 2009 A fundamental limit on the balance of power in a transpiration-controlled channel flow. J. Fluid Mech. 632, 443–446.Google Scholar
Chandrasekhar, S. 1961 Hydrodynamic and Hydromagnetic Stability. Oxford University Press.Google Scholar
Choi, H., Moin, P. & Kim, J. 1991 On the effect of riblets in fully developed laminar channel flows. Phys. Fluids A 3, 1892–1896.CrossRefGoogle Scholar
Chu, D. C. & Karniadakis, G. 1993 A direct numerical simulation of laminar and turbulent flow over riblet-mounted surfaces. J. Fluid Mech. 250, 1–42.CrossRefGoogle Scholar
Fiebig, M. 1995 Embedded vortices in internal flow: heat transfer and pressure loss enhancement. Intl J. Heat Fluid Flow 16, 376–388.Google Scholar
Floryan, J. M. 2012 The thermo-superhydrophobic effect. Bull. Am. Phys. Soc. 57 (1), X50.00015.Google Scholar
Freund, G., Pesch, W. & Zimmermann, W. 2011 Rayleigh–Bénard convection in the presence of spatial temperature modulations. J. Fluid Mech. 673, 318–348.CrossRefGoogle Scholar
Fukugata, K., Sugiyama, K. & Kasagi, N. 2009 On the lower bound of net driving power in controlled duct flows. Physica D 238, 1082–1086.CrossRefGoogle Scholar
Gage, K. S. & Reid, W. H. 1968 The stability of thermally stratified plane Poiseuille flow. J. Fluid Mech. 33, 21–32.Google Scholar
Hossain, M. Z., Floryan, D. & Floryan, J. M. 2012 Drag reduction due to spatial thermal modulations. J. Fluid Mech. 713, 398–419.Google Scholar
Hossain, M. Z. & Floryan, J. M. 2013 Instabilities of natural convection in a periodically heated layer. J. Fluid Mech. 733, 33–67.Google Scholar
Jacobi, A. M. & Shah, R. K. 1998 Air-side flow and heat transfer in compact heat exchangers: a discussion of enhancement mechanisms. Heat Transfer Engng 19, 29–41.CrossRefGoogle Scholar
Joseph, P., Cottin-Bizonne, C., Benoit, J. M., Ybert, C., Journet, C., Tabeling, P. & Bocquet, L. 2006 Slippage of water past superhydrophobic carbon nanotube forests in microchannels. Phys. Rev. Lett. 97, 156104.CrossRefGoogle ScholarPubMed
Kierzenka, J. & Shampine, L. F. 2001 A BVP solver based on residual control and the MATLAB PSE. ACM Trans. Math. Softw. 27, 299–316.CrossRefGoogle Scholar
Kierzenka, J. & Shampine, L. F. 2008 A BVP solver that controls residual and error. J. Numer. Anal. Ind. Appl. Maths 3, 27–41.Google Scholar
Ligrani, P. M., Oliviera, M. M. & Blaskovich, T. 2003 Comparison of heat transfer augmentation techniques. AIAA J. 41, 337–362.CrossRefGoogle Scholar
Mohammadi, A. & Floryan, J. M. 2012 Mechanism of drag generation by surface corrugation. Phys. Fluids 24, 013602.CrossRefGoogle Scholar
Mohammadi, A. & Floryan, J. M. 2013a Pressure losses in grooved channels. J. Fluid Mech. 725, 23–54.Google Scholar
Mohammadi, A. & Floryan, J. M. 2013b Groove optimization for drag reduction. Phys. Fluids 25, 113601.Google Scholar
Orszag, S. A. 1971 Accurate solutions of the Orr–Sommerfeld stability equation. J. Fluid Mech. 50, 689–704.CrossRefGoogle Scholar
Ou, J., Perot, J. B. & Rothstein, J. P. 2004 Laminar drag reduction in microchannels using ultrahydrophobic surfaces. Phys. Fluids 16, 4635–4643.Google Scholar
Ou, J. & Rothstein, J. P. 2005 Direct velocity measurements of the flow past drag-reducing ultrahydrophobic surfaces. Phys. Fluids 17, 103606.CrossRefGoogle Scholar
Quéré, D. 2008 Wetting and roughness. Annu. Rev. Mater. Res. 38, 71–99.CrossRefGoogle Scholar
Reyssat, M., Yeomans, J. M. & Quéré, D. 2008 Impalement of fakir drops. Europhys. Lett. 81, 26006.CrossRefGoogle Scholar
Rothstein, J. P. 2010 Slip on superhydrophobic surfaces. Annu. Rev. Fluid Mech. 42, 89–109.CrossRefGoogle Scholar
Samaha, M. A., Tafreshi, H. V. & Gad-el-Hak, M. 2011 Modeling drag reduction and meniscus stability of superhydrophobic surfaces comprised of random roughness. Phys. Fluids 23, 012001.Google Scholar
Takagi, D. & Balmforth, N. J. 2011 Peristaltic pumping of viscous fluid in an elastic tube. J. Fluid Mech. 672, 196–218.CrossRefGoogle Scholar
Truesdell, R., Mammoli, P., Vorobieff, P., van Swol, P. & Brinker, C. J. 2006 Drag reduction on a patterned superhydrophobic surface. Phys. Rev. Lett. 97, 044504.CrossRefGoogle ScholarPubMed
Yamamoto, A., Hasegawa, Y. & Kasagi, N. 2013 Optimal control of dissimilar heat and momentum transfer in fully developed turbulent channel flow. J. Fluid Mech. 733, 189–230.CrossRefGoogle Scholar
Zhou, M., Li, J., Wu, C., Zhou, X. & Cai, L. 2011 Fluid drag reduction on superhydrophobic surfaces coated with carbon nanotube forest (CNTs). Soft Matt. 7, 4391–4396.Google Scholar