Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-25T12:46:52.157Z Has data issue: false hasContentIssue false
  • English
  • Français

Drag reduction due to spatial thermal modulations

Published online by Cambridge University Press:  26 October 2012

M. Z. Hossain ,
D. Floryan  and
J. M. Floryan
M. Z. Hossain
Affiliation:
Department of Mechanical and Materials Engineering, The University of Western Ontario, London, Ontario, N6A 5B9, Canada
D. Floryan
Affiliation:
Department of Mechanical and Materials Engineering, The University of Western Ontario, London, Ontario, N6A 5B9, Canada
J. M. Floryan*
Affiliation:
Department of Mechanical and Materials Engineering, The University of Western Ontario, London, Ontario, N6A 5B9, Canada
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

It is demonstrated that a significant drag reduction for pressure-driven flows can be realized by applying spatially distributed heating. The heating creates separation bubbles that separate the stream from the bounding walls and, at the same time, alter the distribution of the Reynolds stress, thereby providing a propulsive force. 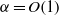The strength of this effect is of practical interest for heating with wavenumbers $\ensuremath{\alpha} = O(1)$ and for flows with small Reynolds numbers and, thus, it is of potential interest for applications in micro-channels. Explicit results given for a very simple sinusoidal heating demonstrate that the drag-reducing effect increases proportionally to the second power of the heating intensity. This increase saturates if the heating becomes too intense. Drag reduction decreases as 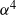${\ensuremath{\alpha} }^{4} $ when the heating wavenumber becomes too small, and as 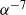${\ensuremath{\alpha} }^{\ensuremath{-} 7} $ when the heating wavenumber becomes too large; this decrease is due to the reduction in the magnitude of the Reynolds stress. The drag reduction can reach up to 87 % for the heating intensities of interest and heating patterns corresponding to the most effective heating wavenumber.

JFM classification

Flow Control: Drag reduction Flow Control: Flow Control Low-Reynolds-number flows: Low-Reynolds-number flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 713 , 25 December 2012 , pp. 398 - 419
Copyright
©2012 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Present address: Department of Mechanical Engineering, Bangladesh University of Engineering and Technology (BUET), Dhaka-1000, Bangladesh.

References

Barthlott, W. & Neinhuis, C. 1977 Purity of sacred lotus, or escape from contamination in biological surfaces. Planta 202, 1–8.Google Scholar
Daniello, R., Waterhouse, N. E. & Rothstein, J. P. 2009 Turbulent drag reduction using superhydrophobic surfaces. Phys. Fluids 21, 085103.Google Scholar
Floryan, J. M. 2012 The thermo-superhydrophobic effect. Bull. Am. Phys. Soc. 57 (1), X50.00015.Google Scholar
Gao, L. & McCarthy, T. J. 2006 A perfectly hydrophobic surface $(\theta (A)/ \theta (R)= 18{0}^{\ensuremath{\circ} } / 18{0}^{\ensuremath{\circ} } )$ . J. Am. Chem. Soc. 128, 9052–9053.CrossRefGoogle Scholar
Joseph, P., Cottin-Bizonne, C., Benoit, J. M., Ybert, C., Journet, C., Tabeling, P. & Bocquet, L. 2006 Slippage of water past superhydrophobic carbon nanotube forests in microchannels. Phys. Rev. Lett. 97, 156104.CrossRefGoogle ScholarPubMed
Krishnan, M., Ugaz, V. M. & Burns, M. A. 2002 PCR in a Rayleigh–Bénard convection cell. Science 298, 793.Google Scholar
Martell, M., Perot, J. B. & Rothstein, J. P. 2009 Direct numerical simulations of turbulent flows over superhydrophobic surfaces. J. Fluid Mech. 620, 31–41.Google Scholar
Mohammadi, A. & Floryan, J. M. 2011 Pressure losses in grooved channels, Expert Systems in Fluid Dynamics Research Laboratory Report ESFD-4/2011, Department of Mechanical and Materials Engineering, The University of Western Ontario.Google Scholar
Mohammadi, A. & Floryan, J. M. 2012 Mechanism of drag generation by surface corrugation. Phys. Fluids 24, 013602.Google Scholar
Ou, J., Perot, J. B. & Rothstein, J. P. 2004 Laminar drag reduction in microchannels using ultrahydrophobic surfaces. Phys. Fluids 16, 4635.Google Scholar
Ou, J. & Rothstein, J. P. 2005 Direct velocity measurements of the flow past drag-reducing ultrahydrophobic surfaces. Phys. Fluids 17, 103606.CrossRefGoogle Scholar
Quéré, D. 2008 Wetting and roughness. Annu. Rev. Mater. Res. 38, 71–99.Google Scholar
Reyssat, M., Yeomans, J. M. & Quéré, D. 2008 Impalement of fakir drops. Europhys. Lett. 81, 26006.Google Scholar
Rothstein, J. P. 2010 Slip on superhydrophobic surfaces. Annu. Rev. Fluid Mech. 42, 89–109.Google Scholar
Samaha, M. A., Tafreshi, H. V. & Gad-el-Hak, 2011 Modelling drag reduction and meniscus stability of superhydrophobic surfaces comprised of random roughness. Phys. Fluids 23, 012001.Google Scholar
Truesdell, R., Mammoli, P., Vorobieff, P., van Swol, P. & Brinker, C. J. 2006 Drag reduction on a patterned superhydrophobic surface. Phys. Rev. Lett. 97, 044504.CrossRefGoogle ScholarPubMed
Xi, Z., Feng, S., Jia, N., Yugui, J. & Zhiqiang, W. 2008 Superhydrophobic surfaces: from structural control to functional application. J. Mater. Chem. 18, 621–633.Google Scholar
Zhou, M., Li, J., Wu, C., Zhou, X. & Cai, L. 2011 Fluid drag reduction on superhydrophobic surfaces coated with carbon nanotube forest (CNTs). Soft Matt. 7, 4391–4396.Google Scholar