Article contents
Drag of a shear-thickening suspension on a rotating cylinder
Published online by Cambridge University Press: 04 September 2023
Abstract
We investigate experimentally the two-dimensional flow of a shear-thickening suspension around a rotating cylinder to which a constant torque is applied. While for low torques both the drag and the flow are steady and close to those for a Newtonian fluid, above the onset torque for discontinuous shear thickening the average velocity of the cylinder saturates and large periodic oscillations of the cylinder velocity are observed. The oscillations result from a hydrodynamic instability of the flow: slow-acceleration phases are followed by high-deceleration phases, triggered by the propagation of a thickening front, and so on. The slow-acceleration phases set the oscillation period, which is limited by the cylinder inertia and inversely proportional to the applied torque. Combined analyses of the cylinder motion and the flow reveal that the front typically nucleates when the shear rate at the cylinder surface reaches the discontinuous shear-thickening threshold. In addition, the characteristics (duration, stress) of the deceleration are set by the interplay between the thickening front propagation and the suspension and cylinder inertiae or the container size. Since for a slow acceleration the shear rate at the cylinder surface is essentially the cylinder angular velocity, this description of the unsteadiness elucidates the saturation of the average velocity. More generally, it illustrates how the hydrodynamics of a shear-thickening suspension with a strongly re-entrant rheology can lead to a marginally re-entrant, although steep, drag curve.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
Rocha et al. Supplementary Movie 1
Real-time movie showing the typical behaviour observed in the high-torque unsteady regime, for a layer of cornstarch suspension subjected to a constant torque ( $\phi = 0.44$, $h = 8$\,mm, $\Gamma = 3.5\Gamma_c$) .
Rocha et al. Supplementary Movie 2
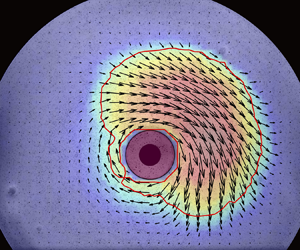
Movie of the thickening-front propagation observed during the cylinder deceleration phase ( $\phi = 0.44$, $h = 35 mm$, $\Gamma = 3.5 \Gamma_c$, same as Fig. 6). The movie starts at the onset of cylinder deceleration ($t = 0$) and finishes at the release time ($t = 124$ ms), when the cylinder starts re-accelerating. Arrows indicate the suspension velocity. Colour encodes the relative norm of the velocity $\sqrt{u_\theta^2 + u_r^2}/R\Omega_c$.
- 2
- Cited by



