Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-16T15:01:52.906Z Has data issue: false hasContentIssue false
  • English
  • Français

Drag coefficient of a rigid spherical particle in a near-critical binary fluid mixture, beyond the regime of the Gaussian model

Published online by Cambridge University Press:  08 January 2020

Shunsuke Yabunaka Open the ORCID record for Shunsuke Yabunaka [Opens in a new window]  and
Youhei Fujitani Open the ORCID record for Youhei Fujitani [Opens in a new window]
Shunsuke Yabunaka*
Affiliation:
Department of Physics, Kyushu University, Fukuoka819-0395, Japan
Youhei Fujitani*
Affiliation:
School of Fundamental Science and Technology, Keio University, Yokohama223-8522, Japan
*
†Email addresses for correspondence: [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

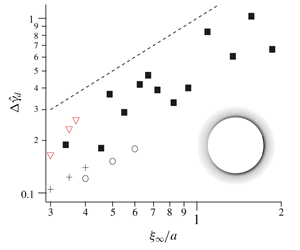
The drag coefficient of a rigid spherical particle deviates from Stokes law when it is put into a near-critical fluid mixture in the homogeneous phase with the critical composition. The deviation ($\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}_{d}$) is experimentally shown to depend approximately linearly on the correlation length of the composition fluctuation far from the particle ($\unicode[STIX]{x1D709}_{\infty }$), and is suggested to be caused by the preferential adsorption between one component and the particle surface. In contrast, the dependence was shown to be much steeper in the previous theoretical studies based on the Gaussian free-energy density. In the vicinity of the particle, especially when the adsorption of the preferred component makes the composition strongly off-critical, the correlation length becomes very small as compared with $\unicode[STIX]{x1D709}_{\infty }$. This spatial inhomogeneity, not considered in the previous theoretical studies, can influence the dependence of $\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}_{d}$ on $\unicode[STIX]{x1D709}_{\infty }$. To examine this possibility, we here apply a renormalized local functional theory, describing the preferential adsorption in terms of the surface field. This theory was previously proposed to explain the interaction of walls immersed in a (near-)critical binary fluid mixture. The free-energy density in this theory, coarse-grained up to the local correlation length, has a very complicated dependence on the order parameter, as compared with the Gaussian free-energy density. Still, a concise expression of the drag coefficient, which was derived in one of the previous theoretical studies, turns out to be valid in the present formulation. We show that, as $\unicode[STIX]{x1D709}_{\infty }$ becomes larger, the dependence of $\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}_{d}$ on $\unicode[STIX]{x1D709}_{\infty }$ becomes distinctly gradual and close to the linear dependence.

JFM classification

Complex Fluids: Colloids Multiphase and Particle-laden Flows: Particle/fluid flow
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 886 , 10 March 2020 , A2
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bal’tsevich, Y. A., Martynets, V. G. & Matizen, E. V. 1967 Brownian motion at the critical point of two-phase liquid-liquid equilibrium. Sov. Phys. JETP 24, 654–658.Google Scholar
Barbot, A. & Araki, T. 2017 Colloidal suspensions in one-phase mixed solvents under shear flow. Soft Matt. 13, 5911–5921.CrossRefGoogle ScholarPubMed
Bedeaux, D. & Mazur, P. 1974 Brownian motion and fluctuating hydrodynamics. Physica A 76, 247–258.Google Scholar
Bertseva, E., Grebenkov, D., Schmidhauser, P., Gribkova, S., Jeney, S. & Forró, L. 2012 Optical trapping microrheology in cultured human cells. Eur. Phys. J. E 35, 63.CrossRefGoogle ScholarPubMed
Beysens, D. 2019 Brownian motion in strongly fluctuating liquid. Thermodynamics Interfaces Fluid Mech. 3, 1–8.Google Scholar
Beysens, D. & Estève, D. 1985 Adsorption phenomena at the surface of silica spheres in a binary liquid mixture. Phys. Rev. Lett. 54, 2123.CrossRefGoogle Scholar
Beysens, D. & Leibler, S. 1982 Observation of an anomalous adsorption in a critical binary mixture. J. Phys. Lett. 43, 133–136.CrossRefGoogle Scholar
Bian, X., Kim, C. & Karniadakis, G. E. 2016 111 years of brownian motion. Soft Matt. 12, 6331–6346.CrossRefGoogle ScholarPubMed
Binder, M. N. 1983 Phase transitions and critical phenomena VIIIV. In Critical Behavior at Surfaces. Academic.Google Scholar
Bonn, D., Otwinowski, J., Sacanna, S., Guo, H., Wegdam, G. & Schall, P. 2009 Direct observation of colloidal aggregation by critical casimir forces. Phys. Rev. Lett. 103, 156101.CrossRefGoogle ScholarPubMed
Brau, R. R., Ferrer, J. M., Lee, H., Castro, C. E., Tam, B. K., Tarsa, P. B., Matsudaira, P., Boyce, M. C., Kamm, R. D. & Lang, M. J. 2007 Passive and active microrheology with optical tweezers. J. Opt. A: Pure Appl. Opt. 9, S103.CrossRefGoogle Scholar
Bray, A. J. & Moore, M. A. 1977 Critical behaviour of semi-infinite systems. J. Phys. A: Math. Gen. 10, 1927.CrossRefGoogle Scholar
Cahn, J. W. 1977 Critical point wetting. J. Chem. Phys. 66, 3667.CrossRefGoogle Scholar
Camley, B. A. & Brown, F. L. H. 2014 Fluctuating hydrodynamics of multicomponent membranes with embedded proteins. J. Chem. Phys. 141, 075103.CrossRefGoogle ScholarPubMed
Cardy, J. 1996 Scaling and Renormalization in Statistical Physics, chap. 7. Cambridge University Press.CrossRefGoogle Scholar
Carey, B. S., Scriven, L. E. & Davis, H. T. 1980 Semiempirical theory of surface tension of binary systems. AIChE J. 26, 705.CrossRefGoogle Scholar
Case, K. M. 1971 Velocity fluctuations of a body in a fluid. Phys. Fluids 14, 2091.CrossRefGoogle Scholar
Chester, W., Breach, D. R. & Proudman, I. 1976 On flow past a sphere at low Reynolds number. J. Fluid Mech. 37, 751–760.CrossRefGoogle Scholar
Cornelisse, P. M. W., Peters, C. J. & de Swaan Arons, J. 1996 Non-classical interfacial tension and fluid phase behaviour. Fluid Phase Equilib. 117, 312–319.CrossRefGoogle Scholar
Diehl, H. W. 1986 Phase transition and critical phenomena X. In Field Theoretical Approach to Critical Behavior at Surfaces. Academic.Google Scholar
Diehl, H. W. 1997 The theory of boundary critical phenomena. Intl J. Mod. Phys. B 11, 3503–3523.CrossRefGoogle Scholar
Diehl, H. W. & Janssen, H. K. 1992 Boundary conditions for the field theory of dynamic critical behavior in semi-infinite systems with conserved order parameter. Phys. Rev. A 45, 7145.CrossRefGoogle ScholarPubMed
Domínguez-García, P., Cardinaux, F., Bertseva, E., Forró, L., Scheffold, F. & Jeney, S. 2014 Accounting for inertia effects to access the high-frequency microrheology of viscoelastic fluids. Phys. Rev. E 90, 060301.Google ScholarPubMed
Einstein, A. 1905 On the motion of small particles suspended in liquids at rest required by the molecular-kinetic theory of heat. Ann. Phys. (Leipzig) 322, 549–560.CrossRefGoogle Scholar
Fisher, M. E. 1968 Renormalization of critical exponents by hidden variables. Phys. Rev. 176, 257.CrossRefGoogle Scholar
Fisher, M. E. & Au-Yang, H. 1980 Critical wall perturbations and a local free energy functional. Physica A 101, 255–264.CrossRefGoogle Scholar
Folk, R. & Moser, G. 1995 Critical dynamics near plait points in mixtures. J. Low Temp. Phys. 99, 11.CrossRefGoogle Scholar
Franosch, T., Grimm, M., Belushkin, M., Mor, F. M., Foffi, G., Forró, L. & Jeney, S. 2011 Resonances arising from hydrodynamic memory in brownian motion. Nature 478, 85–88.CrossRefGoogle ScholarPubMed
Fujitani, Y. 2007 Connection of fields across the interface in the fluid particle dynamics method for colloidal dispersions. J. Phys. Soc. Japan 76, 064401.CrossRefGoogle Scholar
Fujitani, Y. 2014 Effective viscosity of a near-critical binary fluid mixture with colloidal particles dispersed dilutely under weak shear. J. Phys. Soc. Japan 83, 084401.CrossRefGoogle Scholar
Fujitani, Y. 2016 Fluctuation amplitude of a trapped rigid sphere immersed in a near-critical binary fluid mixture within the regime of the gaussian model. J. Phys. Soc. Japan 85, 044401.CrossRefGoogle Scholar
Fujitani, Y. 2017 Undulation amplitude of a fluid membrane in a near-critical binary fluid mixture calculated beyond the gaussian model supposing weak preferential attraction. J. Phys. Soc. Japan 86, 044602.CrossRefGoogle Scholar
Fujitani, Y. 2018 Osmotic effects on dynamics of a colloidal rigid sphere in a near-critical binary fluid mixture. J. Phys. Soc. Japan 87, 084602.CrossRefGoogle Scholar
Furukawa, A., Gambassi, A., Dietrich, S. & Tanaka, H. 2013 Nonequilibrium critical casimir effect in binary fluids. Phys. Rev. Lett. 11, 055701.Google Scholar
de Gennes, P. G. 1979 Scaling Concepts in Polymer Physics, chap. Sect. III. 1. 3. Cornell University Press.Google Scholar
Grebenkov, D. S., Vahabi, M., Bertseva, E., Forró, L. & Jeney, S. 2013 Hydrodynamic and subdiffusive motion of tracers in a viscoelastic medium. Phys. Rev. E 88, 040701.Google Scholar
Grimm, M., Franosch, T. & Jeney, S. 2012 High-resolution detection of brownian motion for quantitative optical tweezers experiments. Phys. Rev. E 86, 021912.Google ScholarPubMed
Gülari, E., Collings, A. F., Schmidt, R. L. & Pings, C. J. 1972 Light scattering and shear viscosity studies of the binary system 2,6-lutidine-water in the critical region. J Chem. Phys. 56, 6169.CrossRefGoogle Scholar
Hohenberg, P. C. & Halperin, B. I. 1977 Theory of dynamic critical phenomena. Rev. Mod. Phys. 49, 435.CrossRefGoogle Scholar
Holyst, R. & Poniewierski, A. 1987 Wetting on a spherical surface. Phys. Rev. B 36, 5628.CrossRefGoogle ScholarPubMed
Huang, R., Chavez, I., Taute, K. M., Lukić, B., Jeney, S., Raizen, M. & Florin, E.-L. 2011 Direct observation of the full transition from ballistic to diffusive brownian motion in a liquid. Nat. Phys. 7, 576–580.CrossRefGoogle Scholar
Hutter, K. & Wang, Y. 2016 Fluid and Thermodynamics: Volume 2: Advanced Fluid Mechanics and Thermodynamic Fundamentals, chap. 11. Springer.Google Scholar
Itami, M. & Sasa, S. 2015 Derivation of Stokes’ law from Kirkwood’s formula and the Green-Kubo formula via large deviation theory. J. Stat. Phys. 161, 532–552.CrossRefGoogle Scholar
Jungk, M., Belkoura, L. & Woermann, D. 1987 Study of a binary critical mixture of 2, 6-dimethyl pyridine/water: measurements of static and dynamic light scattering and specific heat near the lower critical point. Ber. Bunsenges. Phys. Chem. 91, 507–516.CrossRefGoogle Scholar
Kawasaki, K. 1970 Kinetic equations and time correlation functions of critical fluctuations. Ann. Phys. (N.Y.) 61, 1–56.CrossRefGoogle Scholar
Kimura, Y. 2009 Microrheology of soft matter. J. Phys. Soc. Japan 78, 041005.CrossRefGoogle Scholar
Kubo, R., Toda, M. & Hashitsume, N. 1991 Statistical Physics, chap. 1.6. Springer.Google Scholar
Lamb, H. 1932 Hydrodynamics, Sect. 335. Dover.Google Scholar
Lee, S. P. 1976 Evidence for the ‘correlated layer’ effect on the effective viscosity from brownian motion in a ternary liquid mixture. Phys. Rev. Lett. 36, 1319.CrossRefGoogle Scholar
Lorentz, H. A. 1896 A general theorem concerning the motion of a viscous fluid and a few consequences derived from it. Versl. K. Akad. Wet. Amsterdam 5, 168–175.Google Scholar
Lukić, B., Jeney, S., Tischer, C., Kulik, A. J., Forró, L. & Florin, E.-L. 2005 Direct observation of nondiffusive motion of a brownian particle. Phys. Rev. Lett. 95, 160601.CrossRefGoogle ScholarPubMed
Lyons, K. B., Mockler, R. C. & O’Sullivan, W. J. 1973 Light-scattering investigation of brownian motion in a critical mixture. Phys. Rev. Lett. 30, 42.CrossRefGoogle Scholar
Lyons, K. B., Mockler, R. C. & O’Sullivan, W. J. 1974 Brownian motion in a critical mixture: k-dependent diffusion. Phys. Rev. A 10, 393.CrossRefGoogle Scholar
Martynets, V. G. & Matizen, E. V. 1970 Brownian motion near the critical point of the two-phase liquid-liquid equilibrium. Sov. Phys. JETP 31, 228–230.Google Scholar
Mazur, P. & van der Zwan, G. 1978 Brownian motion in a fluid close to its critical point. Physica 92A, 483–500.CrossRefGoogle Scholar
Ohta, T. 1975 Selfconsistent calculation of dynamic critical exponents for classical liquid. Prog. Theor. Phys. 54, 1566–1568.CrossRefGoogle Scholar
Ohta, T. & Kawasaki, K. 1976 Mode coupling theory of dynamic critical phenomena for classical liquids. I: dynamic critical exponents. Prog. Theor. Phys. 55, 1384–1395.CrossRefGoogle Scholar
Okamoto, R., Fujitani, Y. & Komura, S. 2013 Drag coefficient of a rigid spherical particle in a near-critical binary fluid mixture. J. Phys. Soc. Japan 82, 084003.CrossRefGoogle Scholar
Okamoto, R. & Onuki, A. 2012 Casimir amplitudes and capillary condensation of near-critical fluids between parallel plates: renormalized local functional theory. J. Chem. Phys. 136, 114704.CrossRefGoogle ScholarPubMed
Okamoto, R. & Onuki, A. 2013 Attractive interaction and bridging transition between neutral colloidal particles due to preferential adsorption in a near-critical binary mixture. Phys. Rev. E 88, 022309.Google Scholar
Omari, R. A., Grabowski, C. A. & Mukhopadhyay, A. 2009 Effect of surface curvature on critical adsorption. Phys. Rev. Lett. 103, 225705.CrossRefGoogle ScholarPubMed
Onuki, A. 2002 Phase Transition Dynamics. Cambridge University Press.CrossRefGoogle Scholar
Pelisetto, A. & Vicari, E. 2002 Critical phenomena and renormalization-group theory. Phys. Rep. 368, 549–727.CrossRefGoogle Scholar
Pesce, G., Luca, A. C. D., Rusciano, G., Netti, P. A., Fusco, S. & Sasso, A. 2009 Microrheology of complex fluids using optical tweezers: a comparison with macrorheological measurements. J. Opt. A: Pure Appl. Opt. 11, 034016.CrossRefGoogle Scholar
Siggia, E. D., Hohenberg, P. C. & Halperin, B. I. 1976 Renormalization-group treatment of the critical dynamics of the binary-fluid and gas-liquid transitions. Phys. Rev. B 13, 2110.CrossRefGoogle Scholar
Stein, A., Davidson, S. J., Allegra, J. C. & Allen, G. F. 1972 Tracer diffusion and shear viscosity for the system 2,6-lutidine-water near the lower critical point. J. Chem. Phys. 56, 6164.CrossRefGoogle Scholar
Stokes, G. G. 1851 On the effect of the internal friction of fluids on the motion of pendulums. Trans. Camb. Phil. Soc. 9, 8–106.Google Scholar
Sutherland, W. 1905 Lxxv. a dynamical theory of diffusion for non-electrolytes and the molecular mass of albumin. Phil. Mag. 9 (54), 781–785.CrossRefGoogle Scholar
Swinney, H. & Henry, D. L. 1973 Dynamics of fluids near the critical point: Decay rate of order-parameter fluctuations. Phys. Rev. A 8, 2586.CrossRefGoogle Scholar
Tani, H. & Fujitani, Y. 2018 Drag coefficient of a circular inclusion in a near-critical binary fluid membrane drag coefficient of a circular inclusion in a near-critical binary fluid membrane. J. Phys. Soc. Japan 87, 104601.CrossRefGoogle Scholar
Widom, A. 1971 Velocity fluctuations of a hard-core brownian particle. Phys. Rev. A 3, 1394.CrossRefGoogle Scholar
Yabunaka, S., Okamoto, R. & Onuki, A. 2013 Phase separation in a binary mixture confined between symmetric parallel plates: capillary condensation transition near the bulk critical point. Phys. Rev. E 87, 032405.Google Scholar
Yabunaka, S., Okamoto, R. & Onuki, A. 2015 namics in bridging and aggregation of two colloidal particles in a near-critical binary mixture. Soft Matt. 11, 5738.CrossRefGoogle Scholar
Yabunaka, S. & Onuki, A. 2017 Critical adsorption profiles around a sphere and a cylinder in a fluid at criticality: local functional theory. Phys. Rev. E 96, 032127.Google Scholar
van der Zwan, G. & Mazur, P. 1979 Brownian motion in a fluid near its critical point ii: the fluctuation-dissipation theorem. Physica A 98, 169–188.CrossRefGoogle Scholar
Zwanzig, R. & Bixon, M. 1970 Hydrodynamic theory of the velocity correlation function. Phys. Rev. A 2, 2005.CrossRefGoogle Scholar
Zwanzig, R. & Bixon, M. 1975 Compressibility effects in the hydrodynamic theory of Brownian motion. J. Fluid Mech. 69, 21–25.CrossRefGoogle Scholar