Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Giorgio-Serchi, Francesco
and
Weymouth, Gabriel D.
2017.
Soft Robotics: Trends, Applications and Challenges.
Vol. 17,
Issue. ,
p.
37.
Calisti, M.
Picardi, G.
and
Laschi, C.
2017.
Fundamentals of soft robot locomotion.
Journal of The Royal Society Interface,
Vol. 14,
Issue. 130,
p.
20170101.
Giorgio-Serchi, F
Arienti, A
Corucci, F
Giorelli, M
and
Laschi, C
2017.
Hybrid parameter identification of a multi-modal underwater soft robot.
Bioinspiration & Biomimetics,
Vol. 12,
Issue. 2,
p.
025007.
Giorgio-Serchi, Francesco
and
Weymouth, Gabriel D.
2017.
Can added-mass variation act as a thrust force?.
p.
1.
Januddi, Fatihhi Szali
Huzni, Mohd Munsyi
Effendy, Mohamad Shahrul
Bakri, Adnan
Mohammad, Zulhaimi
and
Ismail, Zuhaila
2018.
Development and Testing of Hydraulic Ram Pump (Hydram): Experiments and Simulations.
IOP Conference Series: Materials Science and Engineering,
Vol. 440,
Issue. ,
p.
012032.
Iacoponi, Saverio
Picardi, Giacomo
Chellapurath, Mrudul
Calisti, Marcello
and
Cecilia, Laschi
2018.
Underwater soft jet propulsion based on a hoberman mechanism.
p.
449.
Lidtke, Artur K.
Giorgio-Serchi, Francesco
Lisle, Matt
and
Weymouth, Gabriel D.
2018.
A low-cost experimental rig for multi-DOF unsteady thrust measurements of aquatic bioinspired soft robots.
p.
510.
Giorgio-Serchi, Francesco
Lidtke, Artur K.
and
Weymouth, Gabriel D.
2018.
A Soft Aquatic Actuator for Unsteady Peak Power Amplification.
IEEE/ASME Transactions on Mechatronics,
Vol. 23,
Issue. 6,
p.
2968.
Renda, Federico
Giorgio-Serchi, Francesco
Boyer, Frederic
Laschi, Cecilia
Dias, Jorge
and
Seneviratne, Lakmal
2018.
A unified multi-soft-body dynamic model for underwater soft robots.
The International Journal of Robotics Research,
Vol. 37,
Issue. 6,
p.
648.
Wang, Shuai
He, Guoqiang
and
Qin, Fei
2019.
Research on Skin-Friction Drag Reduction by Hydrogen Injection in Supersonic Boundary Layer.
Xibei Gongye Daxue Xuebao/Journal of Northwestern Polytechnical University,
Vol. 37,
Issue. 3,
p.
449.
Mandre, Shreyas
2020.
Work-minimizing kinematics for small displacement of an infinitely long cylinder.
Journal of Fluid Mechanics,
Vol. 893,
Issue. ,
Aracri, Simona
Giorgio-Serchi, Francesco
Suaria, Giuseppe
Sayed, Mohammed E.
Nemitz, Markus P.
Mahon, Stephen
and
Stokes, Adam A.
2021.
Soft Robots for Ocean Exploration and Offshore Operations: A Perspective.
Soft Robotics,
Vol. 8,
Issue. 6,
p.
625.
Niikura, Takanori
Hosoya, Naoki
Hashimura, Shinji
Kajiwara, Itsuro
and
Giorgio-Serchi, Francesco
2021.
Vibration Engineering for a Sustainable Future.
p.
191.
Hermes, Mark
Ishida, Michael
Luhar, Mitul
and
Tolley, Michael T.
2021.
Bioinspired Sensing, Actuation, and Control in Underwater Soft Robotic Systems.
p.
7.
Ling, Feng
and
Kanso, Eva
2021.
Bioinspired Sensing, Actuation, and Control in Underwater Soft Robotic Systems.
p.
213.
Zhang, Runzhi
Shen, Zhong
Zhong, Hua
Tan, Jiyong
Hu, Yong
and
Wang, Zheng
2021.
A Cephalopod-Inspired Soft-Robotic Siphon for Thrust Vectoring and Flow Rate Regulation.
Soft Robotics,
Vol. 8,
Issue. 4,
p.
416.
Arakawa, Kazuki
Giorgio-Serchi, Francesco
and
Mochiyama, Hiromi
2021.
Snap Pump: A Snap-Through Mechanism for a Pulsatile Pump.
IEEE Robotics and Automation Letters,
Vol. 6,
Issue. 2,
p.
803.
Weymouth, Gabriel D.
and
Giorgio-Serchi, Francesco
2021.
Advances in Critical Flow Dynamics Involving Moving/Deformable Structures with Design Applications.
Vol. 147,
Issue. ,
p.
585.
Zhang, Jun
Lv, Zhichao
Hua, Haobo
Zhang, Chunming
Yu, Haiyang
and
Jiao, Yanmei
2022.
Numerical Study of the Fish-like Robot Swimming in Fluid with High Reynolds Number: Immersed Boundary Method.
Actuators,
Vol. 11,
Issue. 6,
p.
158.
Bi, Xiaobo
and
Zhu, Qiang
2022.
Role of internal flow in squid-inspired jet propulsion.
Physics of Fluids,
Vol. 34,
Issue. 3,
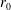 $r_{0}$. A quasi-linear relationship is found to link the terminal amplitude of the oscillations
$r_{0}$. A quasi-linear relationship is found to link the terminal amplitude of the oscillations 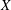 $X$ to the extent of size change
$X$ to the extent of size change  $a$, with
$a$, with 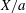 $X/a$ peaking at values from 4 to 4.75 depending on the details of the shape-change kinematics. In addition, it is found that pumping in the frequency range of
$X/a$ peaking at values from 4 to 4.75 depending on the details of the shape-change kinematics. In addition, it is found that pumping in the frequency range of 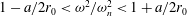 $1-a/2r_{0}<{\it\omega}^{2}/{\it\omega}_{n}^{2}<1+a/2r_{0}$, with
$1-a/2r_{0}<{\it\omega}^{2}/{\it\omega}_{n}^{2}<1+a/2r_{0}$, with 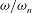 ${\it\omega}/{\it\omega}_{n}$ being the ratio between frequency of actuation and natural frequency, is required for sustained oscillations. The results of this analysis shed light on the role of added-mass recovery in the context of shape-changing bodies and biologically inspired underwater vehicles.
${\it\omega}/{\it\omega}_{n}$ being the ratio between frequency of actuation and natural frequency, is required for sustained oscillations. The results of this analysis shed light on the role of added-mass recovery in the context of shape-changing bodies and biologically inspired underwater vehicles.