Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-09T07:38:28.888Z Has data issue: false hasContentIssue false
  • English
  • Français

Drag and thermophoresis on a sphere in a rarefied gas based on the Cercignani–Lampis model of gas–surface interaction

Published online by Cambridge University Press:  13 August 2020

Denize Kalempa Open the ORCID record for Denize Kalempa [Opens in a new window]  and
Felix Sharipov Open the ORCID record for Felix Sharipov [Opens in a new window]
Denize Kalempa*
Affiliation:
Departamento de Ciências Básicas e Ambientais, Escola de Engenharia de Lorena, Universidade de São Paulo, 12602-810Lorena, Brazil
Felix Sharipov
Affiliation:
Departamento de Física, Universidade Federal do Paraná, Caixa Postal 19044, 81531-990Curitiba, Brazil
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

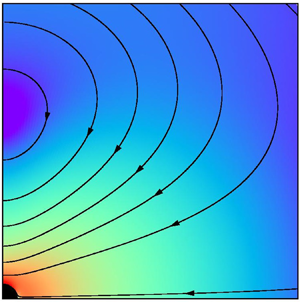
In the present work, the influence of the gas–surface interaction law on the classical problems of viscous drag and thermophoresis on a spherical particle with high thermal conductivity immersed in a monatomic rarefied gas is investigated on the basis of the solution of a kinetic model to the linearized Boltzmann equation. The scattering kernel proposed by Cercignani and Lampis is employed to model the gas–surface interaction law via the setting of two accommodation coefficients, namely the tangential momentum accommodation coefficient and the normal energy accommodation coefficient. The viscous drag and thermophoretic forces acting on the sphere are calculated in a range of the rarefaction parameter, defined as the ratio of the sphere radius to an equivalent free path of gaseous particles, which covers the free molecular, transition and continuum regimes. In the free molecular regime the problem is solved analytically via the method of the characteristics to solve the collisionless kinetic equation, while in the transition and continuum regimes the discrete velocity method is employed to solve the kinetic equation numerically. The numerical calculations are carried out in a range of accommodation coefficients which covers most situations encountered in practice. The macroscopic characteristics of the gas flow around the sphere, namely the density and temperature deviations from thermodynamic equilibrium far from the sphere, the bulk velocity and the heat flux are calculated and their profiles as functions of the radial distance from the sphere are presented for some values of rarefaction parameter and accommodation coefficients. The results show the appearance of the negative thermophoresis in the near-continuum regime and the dependence of this phenomenon on the accommodation coefficients. To verify the reliability of the calculations, the reciprocity relation between the cross phenomena which is valid at an arbitrary distance from the sphere was found and then verified numerically within an accuracy of 0.1 %. The results for the thermophoretic force are compared to the more recent experimental data found in the literature for a copper sphere in argon gas.

JFM classification

Rarefied Gas Flow: Kinetic theory Micro-/Nano-fluid dynamics: Non-continuum effects Compressible Flows: Gas dynamics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 900 , 10 October 2020 , A37
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Allen, M. D. & Raabe, O. G. 1985 Slip correction measurements for solid spherical solid aerosol particles in an improved Millikan apparatus. Aerosol Sci. Technol. 4, 269–286.CrossRefGoogle Scholar
Bailey, C. L., Barber, R. W., Emerson, D. R., Lockerby, D. A. & Reese, J. M. 2004 A critical review on the drag force on a sphere in the transition flow regime. In Proceedings of the 24th International Symposium on Rarefied Gas Dynamics, pp. 743–748. American Institute of Physics.Google Scholar
Beresnev, S. & Chernyak, V. G. 1995 Thermophoresis of a spherical particle in a rarefied-gas: numerical analysis based on the model kinetic equations. Phys. Fluids 7 (7), 1743–1756.CrossRefGoogle Scholar
Beresnev, S. A., Chernyak, V. G. & Fomyagin, G. A. 1990 Motion of a spherical-particle in a rarefied-gas. Part 2. Drag and thermal polarization. J. Fluid Mech. 219, 405–421.CrossRefGoogle Scholar
Bhatnagar, P. L., Gross, E. P. & Krook, M. A. 1954 A model for collision processes in gases. Phys. Rev. 94, 511–525.CrossRefGoogle Scholar
Bird, G. A. 1994 Molecular Gas Dynamics and the Direct Simulation of Gas Flows. Oxford University Press.Google Scholar
Bosworth, R. W., Ventura, A. L., Ketsdever, A. D. & Gimelshein, S. F. 2016 Measurement of negative thermophoretic force. J. Fluid Mech. 805, 207–221.CrossRefGoogle Scholar
Brock, J. R. 1962 On the theory of thermal forces on aerosol particles. J. Colloid Sci. 17, 768–780.CrossRefGoogle Scholar
Cercignani, C. 1972 Scattering kernels for gas-surface interactions. Transp. Theory Stat. Phys. 2 (1), 27–53.CrossRefGoogle Scholar
Cercignani, C. 1975 Theory and Application of the Boltzmann Equation. Scottish Academic Press.Google Scholar
Cercignani, C. 1988 The Boltzmann Equation and its Application. Springer.CrossRefGoogle Scholar
Cercignani, C. & Lampis, M. 1971 Kinetic model for gas-surface interaction. Transp. Theory Stat. Phys. 1, 101–114.CrossRefGoogle Scholar
Chernyak, V. G. & Sograbi, T. V. 2019 The role of molecule-surface interaction in thermophoresis of an aerosol particle. J. Aerosol Sci. 128, 62–71.CrossRefGoogle Scholar
Cunningham, E. 1910 On the velocity of steady fall of spherical particles through fluid medium. Proc. R. Soc. Lond. A 83, 357–365.Google Scholar
De Groot, S. R. & Mazur, P. 1984 Non-Equilibrium Thermodynamics. Dover.Google Scholar
Edmonds, T. & Hobson, J. P. 1965 A study of thermal transpiration using ultrahigh-vacuum techniques. J. Vac. Sci. Technol. 2 (1), 182–197.CrossRefGoogle Scholar
Epstein, M. 1967 A model of the wall boundary condition in kinetic theory. AIAA J. 5 (10), 1797–1800.CrossRefGoogle Scholar
Ferziger, J. H. & Kaper, H. G. 1972 Mathematical Theory of Transport Processes in Gases. North-Holland.Google Scholar
Grad, H. 1949 On the kinetic theory of rarefied gases. Commun. Pure Appl. Maths 2 (4), 331–407.CrossRefGoogle Scholar
Graur, I. A. & Polikarpov, A. P. 2009 Comparison of different kinetic models for the heat transfer problem. Heat Mass Transfer 46 (2), 237–244.CrossRefGoogle Scholar
Hutchinson, D. K., Harper, M. H. & Felder, R. L. 1995 Slip correction measurements for solid spherical particles by modulated light scattering. Aerosol Sci. Technol. 22, 202–212.CrossRefGoogle Scholar
Jacobsen, S. & Brock, J. R. 1965 The thermal force on spherical sodium chloride aerosols. J. Colloid Sci. 20, 544–554.CrossRefGoogle Scholar
Kosuge, S., Aoki, K., Takata, S., Hattori, R. & Sakai, D. 2011 Steady flows of a highly rarefied gas induced by nonuniform wall temperature. Phys. Fluids 23 (3), 030603.CrossRefGoogle Scholar
Krylov, V. I. 2005 Approximate Calculation of Integrals. Dover.Google Scholar
Landau, L. D. & Lifshitz, E. M. 1989 Fluid Mechanics. Pergamon.Google Scholar
Liang, T., Li, Q. & Ye, W. 2013 Performance evaluation of Maxwell and Cercignani–Lampis gas-wall interaction models in the modeling of thermally driven rarefied gas transport. Phys. Rev. E 88 (1), 013009.CrossRefGoogle ScholarPubMed
Loyalka, S. K. 1992 Thermophoretic force on a single-particle. 1. Numerical solution of the linearized Boltzmann equation. J. Aerosol Sci. 23 (3), 291–300.CrossRefGoogle Scholar
Maxwell, J. C. 1879 On stress in rarefied gases arising from inequalities of temperature. Phil Trans. R. Soc. Lond. 170, 231–256.Google Scholar
Naris, S. & Valougeorgis, D. 2005 The driven cavity flow over the whole range of the Knudsen number. Phys. Fluids 17 (9), 097106.CrossRefGoogle Scholar
Ohwada, T. 1996 Heat flow and temperature and density distributions in a rarefied gas between parallel plates with different temperature. Finite-difference analysis of the nonlinear Boltzmann equation for hard-sphere molecules. Phys. Fluids 8, 2153–2160.CrossRefGoogle Scholar
Padrino, J. C., Sprittles, J. E. & Lockerby, D. A. 2019 Thermophoresis of a spherical particle: modelling through moment-based, macroscopic transport equations. J. Fluid Mech. 862, 312–347.CrossRefGoogle Scholar
Podgursky, H. H. & Davis, F. N. 1961 Thermal transpiration at low pressure. The vapor pressure of xenon below 90 K. J. Phys. Chem. 65 (8), 1343–1348.CrossRefGoogle Scholar
Sazhin, O., Kulev, A., Borisov, S. & Gimelshein, S. 2007 Numerical analysis of gas-surface scattering effect on thermal transpiration in the free molecular regime. Vacuum 82 (1), 20–29.CrossRefGoogle Scholar
Sazhin, O. V., Borisov, S. F. & Sharipov, F. 2001 Accommodation coefficient of tangential momentum on atomically clean and contaminated surfaces. J. Vac. Sci. Technol. A 19 (5), 2499–2503,CrossRefGoogle Scholar
Semyonov, Y. G., Borisov, S. F. & Suetin, P. E. 1984 Investigation of heat transfer in rarefied gases over a wide range of Knudsen numbers. Intl J. Heat Mass Transfer 27 (10), 1789–1799.CrossRefGoogle Scholar
Shakhov, E. M. 1967 Boltzmann equation and moment equations in curvilinear coordinates. Fluid Dyn. 2 (2), 107–109.CrossRefGoogle Scholar
Shakhov, E. M. 1968 Generalization of the Krook kinetic relaxation equation. Fluid Dyn. 3 (5), 95–96.CrossRefGoogle Scholar
Sharipov, F. 1999 Non-isothermal gas flow through rectangular microchannels. J. Micromech. Microengng 9 (4), 394–401.CrossRefGoogle Scholar
Sharipov, F. 2003 a Application of the Cercignani–Lampis scattering kernel to calculations of rarefied gas flows. II. Slip and jump coefficients. Eur. J. Mech. B/Fluids 22, 133–143.CrossRefGoogle Scholar
Sharipov, F. 2003 b Application of the Cercignani–Lampis scattering kernel to calculations of rarefied gas flows. III. Poiseuille flow and thermal creep through a long tube. Eur. J. Mech. B/Fluids 22, 145–154.CrossRefGoogle Scholar
Sharipov, F. 2006 Onsager–Casimir reciprocal relations based on the Boltzmann equation and gas-surface interaction law: single gas. Phys. Rev. E 73, 026110.CrossRefGoogle ScholarPubMed
Sharipov, F. 2010 The reciprocal relations between cross phenomena in boundless gaseous systems. Physica A 389, 3743–3760.CrossRefGoogle Scholar
Sharipov, F. 2011 Data on the velocity slip and temperature jump on a gas-solid interface. J. Phys. Chem. Ref. Data 40 (2), 023101.CrossRefGoogle Scholar
Sharipov, F. 2016 Rarefied Gas Dynamics. Fundamentals for Research and Practice. Wiley-VCH.CrossRefGoogle Scholar
Sharipov, F. & Kalempa, D. 2006 Onsager–Casimir reciprocal relations based on the Boltzmann equation and gas-surface interaction: gaseous mixtures. J. Stat. Phys. 125 (3), 661–675.CrossRefGoogle Scholar
Sharipov, F. & Moldover, M. 2016 Energy accommodation coefficient extracted from acoustic resonator experiments. J. Vac. Sci. Technol. A 34 (6), 061604.CrossRefGoogle ScholarPubMed
Sharipov, F. & Strapasson, J. L. 2013 Benchmark problems for mixtures of rarefied gases. I. Couette flow. Phys. Fluids 25, 027101.CrossRefGoogle Scholar
Sharipov, F. M. & Subbotin, E. A. 1993 On optimization of the discrete velocity method used in rarefied gas dynamics. Z. Angew. Math. Phys. 44, 572–577.CrossRefGoogle Scholar
Shen, S. F. 1967 Parametric representation of gas-surface interaction data and the problem of slip-flow boundary conditions with arbitrary accommodation coefficients. Entropie 18, 135.Google Scholar
Siewert, C. E. 2003 The linearized Boltzmann equation: a concise and accurate solution of the temperature-jump problem. J. Quant. Spectrosc. Radiat. Transfer 77, 417–432.CrossRefGoogle Scholar
Siewert, C. E. & Sharipov, F. 2002 Model equations in rarefied gas dynamics: viscous-slip and thermal-slip coefficients. Phys. Fluids 14 (12), 4123–4129.CrossRefGoogle Scholar
Sone, Y. 1966 Thermal creep in rarefied gas. J. Phys. Soc. Japan 21, 1836–1837.CrossRefGoogle Scholar
Sone, Y. 1972 Flow induced by thermal stress in rarefied gas. Phys. Fluids 15, 1418–1423.CrossRefGoogle Scholar
Sone, Y. 2007 Molecular Gas Dynamics. Theory, Techniques and Applications. Birkhäuser.CrossRefGoogle Scholar
Sone, Y. & Aoki, K. 1983 A similarity solution of the linearized Boltzmann equation with application to thermophoresis of a spherical particle. J. Mec. Theor. Appl. 2 (1), 3–12.Google Scholar
Sone, Y. & Takata, S. 1992 Discontinuity of the velocity distribution function in a rarefied gas around a convex body and the S layer at the bottom of the Knudsen layer. Transp. Theory Stat. Phys. 21 (4–6), 501–530.CrossRefGoogle Scholar
Spijker, P., Markvoort, A. J., Nedea, S. V. & Hilbers, P. A. J. 2010 Computation of accommodation coefficients and the use of velocity correlation profiles in molecular dynamics simulations. Phys. Rev. E 81, 011203.CrossRefGoogle ScholarPubMed
Stokes, G. G. 1845 On the theories of the internal friction of fluids in motion and of the equilibrium and motion of elastic solids. Trans. Camb. Phil. Soc. 8, 287–319.Google Scholar
Struchtrup, H. & Torrilhon, M. 2003 Regularization of Grad's 13-moment equations: derivation and linear analysis. Phys. Fluids 15, 2668.CrossRefGoogle Scholar
Takata, S., Aoki, K. & Sone, Y. 1992 Thermophoresis of a sphere with a uniform temperature: numerical analysis of the Boltzmann equation for hard-sphere molecules. In Rarefied Gas Dynamics: Theory and Simulations (ed. Shizgal, B. D. & Weaver, D. P.), pp. 626–639. Progress in Astronautics and Aeronautics. AIAA.Google Scholar
Takata, S. & Sone, Y. 1995 Flow induced around a sphere with a non-uniform surface temperature in a rarefied gas, with application to the drag and thermal force problem of a spherical particle with an arbitrary thermal conductivity. Eur. J. Mech. B/Fluids 14 (4), 487–518.Google Scholar
Takata, S., Sone, Y. & Aoki, K. 1993 Numerical analysis of a uniform flow of a rarefied gas past a sphere on the basis of the Boltzmann equation for hard-sphere molecules. Phys. Fluids A 5 (3), 716–737.CrossRefGoogle Scholar
Torrilhon, M. 2010 Slow gas microflow past a sphere: analytical solution based on moment equations. Phys. Fluids 22 (7), 072001.CrossRefGoogle Scholar
Trott, W. M., Castaneda, J. N., Torczynski, J. R., Gallis, M. A. & Rader, D. J. 2011 An experimental assembly for precise measurement of thermal accommodation coefficients. Rev. Sci. Instrum. 82 (3), 035120.CrossRefGoogle ScholarPubMed
Vogel, E., Jaeger, B., Hellmann, R. & Bich, E. 2010 Ab initio pair potential energy curve for the argon atom pair and thermophysical properties for the dilute argon gas. II. Thermophysical properties for low-density argon. Mol. Phys. 108 (24), 3335–3352.CrossRefGoogle Scholar
Wu, L. & Struchtrup, H. 2017 Assessment and development of the gas kinetic boundary condition for the Boltzmann equation. J. Fluid Mech. 823, 511–537.CrossRefGoogle Scholar
Yakunchikov, A. N., Kovalev, V. L. & Utyuzhnikov, S. V. 2012 Analysis of gas-surface scattering models based on computational molecular dynamics. Chem. Phys. Lett. 554, 225–230.CrossRefGoogle Scholar
Yamamoto, K. & Ishihara, Y. 1988 Thermophoresis of a spherical-particle in a rarefied-gas of a transition regime. Phys. Fluids 31 (12), 3618–3624.CrossRefGoogle Scholar
Yamamoto, K., Takeuchi, H. & Hyakutake, T. 2007 Scattering properties and scattering kernel based on the molecular dynamics analysis of gas-wall interaction. Phys. Fluids 19, 087102.CrossRefGoogle Scholar
Young, J. B. 2011 Thermophoresis of a sphercial particle: reassessment, clarifications, and new analysis. Aerosol Sci. Technol. 45, 927–948.CrossRefGoogle Scholar
Zheng, F. 2002 Thermophoresis of spherical and non-spherical particles: a review of theories and experiments. Adv. Colloid Interface Sci. 97 (1–3), 255–278.CrossRefGoogle ScholarPubMed
Supplementary material: PDF

Kalempa and Sharipov supplementary material

Figures S1-S6

Download Kalempa and Sharipov supplementary material(PDF)
PDF 227.9 KB