Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-01-09T22:04:17.106Z Has data issue: false hasContentIssue false
  • English
  • Français

Dissipation-scale fluctuations and mixing transition in turbulent flows

Published online by Cambridge University Press:  10 July 2008

VICTOR YAKHOT
VICTOR YAKHOT*
Affiliation:
Department of Aerospace and Mechanical Engineering, Boston University, Boston, MA 02215, USA
Get access Rights & Permissions [Opens in a new window]

Abstract

A small separation between reactants, not exceeding 10−8 − 10−7 cm, is the necessary condition for various chemical reactions. It is shown that random advection and stretching by turbulence leads to the formation of scalar-enriched sheets of strongly fluctuating thickness ηc. The molecular-level mixing is achieved by diffusion across these sheets (interfaces) separating the reactigants. Since the diffusion time scale is 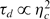, knowledge of the probability density Q(ηc, Re) is crucial for evaluation of mixing times and chemical reaction rates. According to Kolmogorov–Batchelor phenomenology, the stretching time τeddy ≈ L/urms = O(1) is independent of large-scale Reynolds number Re = urmsL/ν and the diffusion time 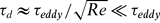is very small. Therefore, in previous studies, molecular diffusion was frequently neglected as being too fast to contribute substantially to the reaction rates. In this paper, taking into account strong intermittent fluctuations of the scalar dissipation scales, this conclusion is re-examined. We derive the probability density Q(ηc, Re, Sc), calculate the mean scalar dissipation scale and predict transition in the reaction rate behaviour from 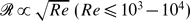to the high-Re asymptotics 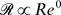. These conclusions are compared with known experimental and numerical data.

Type
Papers
Information
Journal of Fluid Mechanics , Volume 606 , 10 July 2008 , pp. 325 - 337
Copyright
Copyright © Cambridge University Press 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Batchelor, G. K. 1959 Small-scale variation of convected quantities like temperature in turbulent fluid. General discussion and the case of small conductivity. J. Fluid Mech. 5, 113–133.CrossRefGoogle Scholar
Bilger, R. W. 2004 Some aspects of scalar dissipation. Flow, Turbul. Combust. 72, 93–114.CrossRefGoogle Scholar
Buch, K. A. & Dahm, W. J. 1998 Experimental study of the fine scale structure of conserved scalar mixing in turbulent shear flows. Part 2. J. Fluid Mech. 364, 1–29.CrossRefGoogle Scholar
Celani, A, Cencini, M, Vergassola, M, Villermaux, E. & Vincenzi, D. 2005 Shear effects on passive scalar spectra. J. Fluid Mech. 523, 99–108.CrossRefGoogle Scholar
Chertkov, M., Falkovich, G. & Kolokolov, I. 1998 Intermittent dissipation of a passive scalar in turbulence. Phys. Rev. Lett. 80, 2121–2121.CrossRefGoogle Scholar
Dimotakis, P. E. 2005 Turbulent mixing. Annu. Rev. Fluid Mech. 37, 329–356.CrossRefGoogle Scholar
Dimotakis, P. E. 1993 Some issues on turbulence and turbulent mixing. CALCIT Rep. FM93-1.Google Scholar
Duchon, J. & Robert, R. 2000 Inertial energy dissipation for weak solutions of incompressible Euler and Navier-Stokes equations. Nonlinearity 13, 249–255.CrossRefGoogle Scholar
Eyink, G. L. 2003 Local 4/5-law and energy dissipation anomaly in turbulence. Nonlinearity 16, 137–145.CrossRefGoogle Scholar
Gamba, A. & Kolokolov, I. 1999 Dissipation statistics of a passive scalar in a multidimensional smooth flow. J. Statist. Phys. 94, 759–777.CrossRefGoogle Scholar
Gotoh, T. & Nakano, T. 2003 Role of pressure in turbulence. J. Statist. Phys. 113, 855–874.CrossRefGoogle Scholar
Kushnir, D., Schumacher, J. & Brandt, A. 2006 Geometry of intensive dissipation events in turbulence. Phys. Rev. Lett. 97, 124502–124505.CrossRefGoogle ScholarPubMed
Landau, L. D. & Lifshitz, E. M. 1959 Fluid Mechanics. Pergamon.Google Scholar
Monin, A. S. & Yaglom, A. M. 1975 Statistical Fluid Mechanics, vol. 2, p. 435. MIT Press.Google Scholar
Paladin, P. & Vulpiani, A. 1987 Anomalous scaling laws in multifractal objects. Phys. Rep. 156, 147–225.CrossRefGoogle Scholar
Peters, N. 2000 Turbulent Combustion. Cambridge University Press.CrossRefGoogle Scholar
Polyakov, A. M. 1995 Turbulence without pressure Phys. Rev. E 52, 6183–6188.Google ScholarPubMed
Schumacher, J. & Sreenivasan, K. R. 2003 Geometric features of the mixing of passive scalars at high Schmidt numbers. Phys. Rev. Lett. 91, 174501–174505.CrossRefGoogle ScholarPubMed
Schumacher, J. 2007 Sub-Kolmogorov-scale fluctuations in fluid turbulence. Europhys. Lett. 80, 54001.CrossRefGoogle Scholar
Schumacher, J, Sreenivasan, K. R. & Yeung, P. K. 2005 Very fine structures in scalar mixing. J. Fluid Mech. 531, 113–122.CrossRefGoogle Scholar
Schumacher, J, Sreenivasan, K. R. & Yakhot, V. 2007 Asymptotic exponents from low-Reynolds-number flows. New. J. Phys. 9, 1–19.CrossRefGoogle Scholar
Sreenivasan, K. R. 2004 Possible effects of small-scale intermittency in turbulent reacting flows. Flow, Turbul. Combust. 72, 115–131.CrossRefGoogle Scholar
Schumacher, J. 2007, (private communication).Google Scholar
Tcheou, J. M., Brachet, M. E., Belin, F., Tabeling, P. & Wiliaime, H. 1999 Multifractal asymptotic modeling of the probability density function of velocity increment in turbulence. Physica D 129, 93–114.Google Scholar
Villermaux, E., Innocenti, C. & Duplat, J. 2001 Short circuits in the Corrsin-Obukhov cascade. Phys. Fluids 13, 284–289.CrossRefGoogle Scholar
Villermaux, E. & Meunier, P. 2003 How vortices mix. J. Fluid Mech. 476, 213–222.Google Scholar
Villermaux, E. & Duplat, J. 2006 Coarse grained scale of turbulent mixtures. Phys. Rev. Lett. 97, 144506–144509.CrossRefGoogle ScholarPubMed
Wang, L. & Peters, N. 2006 The length scale distribution function of the distance between extremal points in passive scalar turbulence. J. Fluid Mech. 554, 457–475.CrossRefGoogle Scholar
Yakhot, V. & Sreenivasan, K. R. 2004 Toward dynamical theory of multifractals in turbulence Physica A 343, 147–155.CrossRefGoogle Scholar
Yakhot, V. & Sreenivasan, K. R. 2005 Anomalous scaling of structure functions and dynamic constraint on turbulence simulations. J. Statist. Phys. 121, 823–841.CrossRefGoogle Scholar
Yakhot, V. 2006 Probability densities in strong turbulence. Physica D 215, 166–174.Google Scholar
Yakhot, V. 2003 Pressure-velocity correlations and anomalous exponents of structure functions in turbulence. J. Fluid Mech. 495 135–143.CrossRefGoogle Scholar