Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-01-24T22:01:13.708Z Has data issue: false hasContentIssue false
  • English
  • Français

Dispersion coefficient in an electro-osmotic flow of a viscoelastic fluid through a microchannel with a slowly varying wall zeta potential

Published online by Cambridge University Press:  29 January 2018

J. C. Arcos ,
F. Méndez Open the ORCID record for F. Méndez [Opens in a new window] ,
E. G. Bautista Open the ORCID record for E. G. Bautista [Opens in a new window]  and
O. Bautista Open the ORCID record for O. Bautista [Opens in a new window]
J. C. Arcos
Affiliation:
ESIME Azcapotzalco, Instituto Politécnico Nacional, Av. de las Granjas No. 682, Col. Santa Catarina, Del. Azcapotzalco, Ciudad de México 02250, Mexico
F. Méndez
Affiliation:
Departamento de Termofluidos, Facultad de Ingeniería, UNAM, Ciudad de México 04510, Mexico
E. G. Bautista
Affiliation:
ESIME Azcapotzalco, Instituto Politécnico Nacional, Av. de las Granjas No. 682, Col. Santa Catarina, Del. Azcapotzalco, Ciudad de México 02250, Mexico
O. Bautista*
Affiliation:
ESIME Azcapotzalco, Instituto Politécnico Nacional, Av. de las Granjas No. 682, Col. Santa Catarina, Del. Azcapotzalco, Ciudad de México 02250, Mexico
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

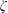The dispersion coefficient of a passive solute in a steady-state pure electro-osmotic flow (EOF) of a viscoelastic liquid, whose rheological behaviour follows the simplified Phan-Thien–Tanner (sPTT) model, along a parallel flat plate microchannel, is studied. The walls of the microchannel are assumed to have modulated and low $\unicode[STIX]{x1D701}$ potentials, which vary slowly in the axial direction in a sinusoidal manner. The flow field required to obtain the dispersion coefficient was solved using the lubrication approximation theory (LAT). The solution of the electric potential is based on the Debye–Hückel approximation for a symmetric 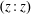$(z:z)$ electrolyte. The viscoelasticity of the fluid is observed to notably amplify the axial distribution of the effective dispersion coefficients due to the variation in the 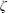$\unicode[STIX]{x1D701}$ potentials of the walls. The problem was formulated for two cases: when the Debye layer thickness (EDL) was on the order of unity (thick EDL) and in the limit where the thickness of the EDL was very small compared with the height of the microchannel (thin EDL limit). Due to the coupling between the nonlinear governing equations and the sPTT fluid model, they were replaced by their approximate linearized forms and solved in the limit of 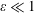$\unicode[STIX]{x1D700}\ll 1$ using the regular perturbation technique. Here $\unicode[STIX]{x1D700}$ is the amplitude of the sinusoidal function of the 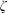$\unicode[STIX]{x1D701}$ potentials. Additionally, the numerical solution of the simplified governing equations was also obtained for 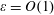$\unicode[STIX]{x1D700}=O(1)$ and compared with the approximate solution, showing excellent agreement for 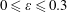$0\leqslant \unicode[STIX]{x1D700}\leqslant 0.3$. Note that the dispersion coefficient primarily depends on the Deborah number, on the ratio of the half-height of the microchannel to the Debye length, and on the assumed variation in the 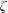$\unicode[STIX]{x1D701}$ potentials of the walls.

JFM classification

Low-Reynolds-number flows: Low-Reynolds-number flows Low-Reynolds-number flows: Lubrication theory Micro-/Nano-fluid dynamics: Micro-/Nano-fluid dynamics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 839 , 25 March 2018 , pp. 348 - 386
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Afonso, A. M., Alves, M. A. & Pinho, F. T. 2009 Analytical solution of mixed electro-osmotic/pressure driven flows of viscoelastic fluids in microchannels. J. Non-Newton. Fluid Mech. 159, 50–63.CrossRefGoogle Scholar
Ajdari, A. 1995 Electro-osmosis on inhomogeneously charged surfaces. Phys. Rev. Lett. 75, 755–758.CrossRefGoogle ScholarPubMed
Ajdari, A. 1996 Generation of transverse fluid currents and forces by an electric field: electro-osmosis on charge-modulated and undulated surfaces. Phys. Rev. E 53, 4996–5005.Google ScholarPubMed
Ajdari, A., Bontoux, N. & Stone, H. A. 2006 Hydrodynamic dispersion in shallow microchannels: the effect of cross-sectional shape. Anal. Chem. 78, 387–392.CrossRefGoogle ScholarPubMed
Anderson, J. L. & Idol, W. K. 1985 Electroosmosis through pores with nonuniformly charged walls. Chem. Engng Commun. 38, 93–106.CrossRefGoogle Scholar
Aris, R. 1956 On the dispersion of a solute in a fluid flowing through a tube. Proc. R. Soc. Lond. A 235, 67–77.Google Scholar
Aris, R. 1959 On the dispersion of a solute by diffusion, convection and exchange between phases. Proc. R. Soc. Lond. A 252, 538–550.Google Scholar
Bautista, O., Sánchez, S., Arcos, J. C. & Méndez, F. 2013 Lubrication theory for electro-osmotic flow in a slit microchannel with the Phan-Thien and Tanner model. J. Fluid Mech. 722, 496–532.CrossRefGoogle Scholar
Bender, C. M. & Orszag, S. A. 1999 Advanced Mathematical Methods for Scientists and Engineers I: Asymptotic Methods and Perturbation Theory. Springer.CrossRefGoogle Scholar
Burgreen, D. & Nakache, F. R. 1964 Electrokinetic flow in ultrafine capillary slits. J. Phys. Chem. 68 (5), 1084–1091.CrossRefGoogle Scholar
Chang, H.-C. & Yeo, L. Y. 2010 Electrokinetically Driven Microfluidics and Nanofluidics. Cambridge University Press.Google Scholar
Cho, C. C., Chen, C. L. & Chen, C. K. 2012a Mixing enhancement of electrokinetically-driven non-Newtonian fluids in microchannel with patterned blocks. Chem. Engng J. 191, 132–140.CrossRefGoogle Scholar
Cho, C. C., Chen, C. L. & Chen, C. K. 2012b Mixing of non-Newtonian fluids in wavy serpentine microchannel using electrokinetically driven flow. Electrophoresis 33, 743–750.CrossRefGoogle ScholarPubMed
Cho, C. C., Ho, C. J. & Chen, C. K. 2010 Enhanced micromixing of electroosmotic flows using aperiodic time-varying zeta potentials. Chem. Engng J. 163, 180–187.CrossRefGoogle Scholar
Datta, S. & Ghosal, S. 2008 Dispersion due to wall interactions in microfluidic separation systems. Phys. Fluids 20, 012103.CrossRefGoogle Scholar
Datta, S. & Ghosal, S. 2009 Characterizing dispersion in microfluidic channels. Lab on a Chip 9, 2537–2550.CrossRefGoogle ScholarPubMed
Datta, S., Ghosal, S. & Patankar, N. A. 2006 Electroosmotic flow in a rectangular channel with variable wall zeta-potential: comparison of numerical simulation with asymptotic theory. Electrophoresis 27, 611–619.CrossRefGoogle Scholar
Deemter, J. J. Van, Zuiderweg, F. J. & Klinkenberg, A. 1956 Longitudinal diffusion and resistance to mass transfer as causes of nonideality in chromatography. Chem. Engng Sci. 5, 271–289.CrossRefGoogle Scholar
Dutta, D., Ramachandran, A. & Leighton, D. T. 2006 Effect of channel geometry on solute dispersion in pressure-driven microfluidic systems. Microfluid. Nanofluid. 2, 275–2909.CrossRefGoogle Scholar
Dutta, P. & Beskok, A. 2001 Analytical solution of combined electroosmotic/pressure driven flows in two-dimensional straight channels: finite Debye layer effects. Anal. Chem. 73, 1979–1986.CrossRefGoogle ScholarPubMed
Ferrás, L. L., Afonso, A. M., Alves, M. A., Nóbrega, J. M. & Pinho, F. T. 2014 Analytical and numerical study of the electro-osmotic annular flow of viscoelastic fluids. J. Colloid Interface Sci. 420, 152–157.CrossRefGoogle ScholarPubMed
Fuest, M., Boone, C., Rangharajan, K. K., Conlisk, A. T. & Prakash, S. 2015 A three-state nanofluidic field effect switch. Nano Lett. 15, 2365–2371.CrossRefGoogle ScholarPubMed
Fuest, M., Rangharajan, K. K., Boone, C., Conlisk, A. T. & Prakash, S. 2017 Cation dependent surface charge regulation in gated nanofluidic devices. Anal. Chem. 89, 1593–1601.CrossRefGoogle ScholarPubMed
Ghosal, S. 2002 Lubrication theory for electro-osmotic flow in a microfluidic channel of slowly varying cross-section and wall charge. J. Fluid Mech. 459, 103–128.CrossRefGoogle Scholar
Ghosal, S. 2003 The effect of wall interactions in capillary-zone electrophoresis. J. Fluid Mech. 491, 285–300.CrossRefGoogle Scholar
Ghosh, U. & Chakraborty, S. 2015 Electroosmosis of viscoelastic fluids over charge modulated surfaces in narrow confinements. Phys. Fluids 27, 062004.CrossRefGoogle Scholar
Goodwine, B. 2011 Engineering Differential Equations: Theory and Applications. Springer.CrossRefGoogle Scholar
Griffiths, S. K. & Nilson, R. H. 1999 Hydrodynamic dispersion of a neutral nonreacting solute in electroosmotic flow. Anal. Chem. 71, 5522–5529.CrossRefGoogle Scholar
Hadigol, M., Nosrati, R., Nourbakhsh, A. & Raisee, M. 2011 Numerical study of electroosmotic micromixing of non-newtonian fluids. J. Non-Newtonian Fluid Mech. 166, 965–971.CrossRefGoogle Scholar
Herr, A. E., Molho, J. I., Santiago, J. G., Mungal, M. G. & Kenny, T. W. 2000 Electroosmotic capillary flow with nouniform zeta potential. Anal. Chem. 72, 1053–1057.CrossRefGoogle Scholar
Hoffman, J. D. 1992 Numerical Methods for Enginners and Scientists. McGraw-Hill.Google Scholar
Hoshyargar, V., Ashrafizadeh, S. N. & Sadeghi, A. 2017 Mass transport characteristics of diffusioosmosis: potential applications for liquid phase transportation and separation. Phys. Fluids 29, 012001.CrossRefGoogle Scholar
Jaluria, Y. & Torrance, K. E. 2003 Computational Heat Transfer. Taylor & Francis.Google Scholar
Karniadakis, George, Beskok, Ali & Aluru, Narayan 2005 Microflows and Nanoflows. Fundamentals and Simulation. Springer.Google Scholar
Karnik, R. & Castelino, K. 2006 Field-effect control of protein transport in a nanofluidic transistor circuit. Appl. Phys. Lett. 88, 123114.CrossRefGoogle Scholar
Karnik, R., Castelino, K., Fan, R., Yang, P. & Majumdar, A. 2005a Effects of biological reactions and modifications on conductance of nanofluidic channels. Nano Lett. 5 (9), 1638–1642.CrossRefGoogle ScholarPubMed
Karnik, R., Duan, C., Castelino, K., Daiguji, H. & Majumdar, A. 2007 Rectification of ionic current in a nanofluidic diode. Nano Lett. 7 (3), 547–551.CrossRefGoogle Scholar
Karnik, R., Fan, R., Yue, M., Li, D., Yang, P. & Majumdar, A. 2005b Electrostatic control of ions and molecules in nanofluidic transistors. Nano Lett. 5 (5), 943–948.CrossRefGoogle ScholarPubMed
Kwak, H. S., Kim, H., Hyun, J. M. & Song, T. H. 2009 Thermal control of electroosmotic flow in a microchannel through temperature-dependent properties. J. Colloid Interface Sci. 335, 123–129.CrossRefGoogle Scholar
Leal, L. G. 2007 Advanced Transpor Phenomena: Fluid Mechanics and Convective Transport Processes. Cambridge University Press.CrossRefGoogle Scholar
Lee, C. Y., Lee, G. B., Fu, L. M., Lee, K. H. & Yang, R. J. 2004a Electrokinetically driven active micromixers utilizing zeta potential variation induced by field effect. J. Micromech. Microengng 14, 1879–1887.CrossRefGoogle Scholar
Levine, S., Marriott, J. R. & Neale, G. 1975 Theory of electrokinetic flow in fine cylindrical capillaries at high zeta-potentials. J. Colloid Interface Sci. 52, 136–149.CrossRefGoogle Scholar
Masliyah, J. H. & Bhattacharjee, S. 2006 Electrokinetic and Colloid Transport Phenomena. Wiley-Interscience.CrossRefGoogle Scholar
Mei, C. C., Auriault, J. L. & Ng, C. O. 1996 Some applications of the homogenization theory. Adv. Appl. Mech. 32, 277–348.CrossRefGoogle Scholar
Mei, C. C. & Vernescu, B. 2010 Homogenization Methods for Multiscale Mechanics. World Scientific.CrossRefGoogle Scholar
Molho, J. I., Herr, A. E., Mosier, B. P., Santiago, J. G., Kenny, T. W., Brennen, R. A. & Mohammadi, B. 2001 Optimization of turn geometries for microchip electrophoresis. Anal. Chem. 73, 1350–1360.CrossRefGoogle Scholar
Newman, J. & Thomas-Alyea, K. E. 2004 Electrochemical Systems. Wiley.Google Scholar
Ng, C. O. & Chen, B. 2013 Dispersion in electro-osmotic flow through a slit channel with axial step changes of zeta potential. Trans. ASME J. Fluids Engng 135, 101203.CrossRefGoogle Scholar
Ng, C. O. & Qi, C. 2014 Electroosmotic flow of a power-law fluid in a non-uniform microchannel. J. Non-Newtonian Fluid Mech. 208–209, 118–125.CrossRefGoogle Scholar
Ng, C. O. & Zhou, Q. 2012a Dispersion due to electroosmotic flow in a circular microchannel with slowly varying wall potential and hydrodynamic slippage. Phys. Fluids 24, 112002.CrossRefGoogle Scholar
Ng, C. O. & Zhou, Q. 2012b Electro-osmotic flow through a thin channel with gradually varying wall potential and hydrodynamic slippage. Fluid Dyn. Res. 44, 055507.CrossRefGoogle Scholar
Nguyen, N. T. 2012 Micromixers. Fundamentals, Design and Fabrication. William Andrew.Google Scholar
Paul, S. & Ng, C. O. 2012 Dispersion in electroosmotic flow generated by oscillatory electric field interacting with oscillatory wall potentials. Microfluid. Nanofluid. 12, 237–256.CrossRefGoogle Scholar
Prakash, S. & Conlisk, A. T. 2016 Field effect nanofluidics. Lab on a Chip 16, 3855–3865.CrossRefGoogle ScholarPubMed
Prakash, S., Karacor, M. B. & Banerjee, S. 2009 Surface modification in microsystems and nanosystems. Surf. Sci. Rep. 64, 233–254.CrossRefGoogle Scholar
Prakash, S. & Karacor, M. B. 2011 Characterizing stability of ‘click’ modified glass surfaces to common microfabrication conditions and aqueous electrolyte solutions. Nanoscale 3, 3309–3315.CrossRefGoogle ScholarPubMed
Prakash, S., Zambrano, H. A., Fuest, M., Boone, C., Kim, E. R., Vasquez, N. & Conlisk, A. T. 2015 Electrokinetic transport in silica nanochannels with asymmetric surface charge. Microfluid. Nanofluid. 19, 1455–1464.CrossRefGoogle Scholar
Probstein, R. F. 2003 Physicochemical Hydrodynamics: An Introduction. Wiley.Google Scholar
Qi, C. & Ng, C. O. 2015 Electroosmotic flow of a power-law fluid through an asymmetrical slit microchannel with gradually varying wall shape and wall potential. Colloids Surf. A 472, 26–37.CrossRefGoogle Scholar
Rice, C. L. & Whitehead, R. 1965 Electrokinetic flow in a narrow cylindrical capillary. J. Phys. Chem. 69 (11), 4017–4024.CrossRefGoogle Scholar
Schasfoort, R. B. M., Schlautmann, S., Hendrikse, J. & van den Berg, A. 1999 Field-effect flow control for microfabricated fluidic networks. Science 286, 942–945.CrossRefGoogle ScholarPubMed
von Smoluchowski, M. 1917 Versuch einer mathematischen Theorie der Koagulationskinetik kolloider Lösungen. Z. Phys. Chem. 92, 129–135.Google Scholar
Stone, H. A., Stroock, A. D. & Ajdari, A. 2004 Engineering flows in small devices: microfluidics toward a lab-on-a-chip. Annu. Rev. Fluid Mech. 36, 381–411.CrossRefGoogle Scholar
Taylor, G. I. 1953 Dispersion of solute matter in solvent flowing slowly through a tube. Proc. R. Soc. Lond. A 219, 186–203.Google Scholar
Thien, N. P. & Tanner, R. I. 1977 A new constitutive equation derived from network theory. J. Non-Newton. Fluid Mech. 2, 353–365.CrossRefGoogle Scholar
Tripathi, A., Bozkurt, O. & Chauhan, A. 2005 Dispersion in microchannels with temporal temperature variations. Phys. Fluids 17, 103607.CrossRefGoogle Scholar
Vargas, C., Arcos, J., Bautista, O. & Méndez, F. 2017 Hydrodynamic dispersion in a combined magnetohydrodynamic- electroosmotic-driven flow through a microchannel with slowly varying wall zeta potentials. Phys. Fluids 29, 092002.CrossRefGoogle Scholar
Vasu, N. & De, S. 2010 Electroosmotic flow of power-law fluids at high zeta potentials. Colloids Surf. A 368, 44–52.CrossRefGoogle Scholar
Zambrano, H. A., Pinti, M., Conlisk, A. T. & Prakash, S. 2012 Electrokinetic transport in a water-chloride nanofilm in contact with a silica surface with discontinuous charged patches. Microfluid. Nanofluid. 13, 735–747.CrossRefGoogle Scholar
Zhao, C., Zholkovskij, E., Masliyah, J. H. & Yang, C. 2008 Analysis of electroosmotic flow of power-law fluids in a slit microchannel. J. Colloid Interface Sci. 326, 503–510.CrossRefGoogle Scholar
Zholkovskij, E. K. & Masliyah, J. H. 2004 Hydrodynamic dispersion due to combined pressure-driven and electroosmotic flow through microchannels with a thin double layer. Anal. Chem. 76, 2708–2718.CrossRefGoogle ScholarPubMed
Zholkovskij, E. K., Masliyah, J. H. & Czarnecki, J. 2003 Electroosmotic dispersion in microchannels with a thin double layer. Anal. Chem. 75, 901–909.CrossRefGoogle ScholarPubMed
Zholkovskij, E. K., Masliyah, J. H. & Yaroshchuk, A. E. 2013 Broadening of neutral analyte band in electroosmotic flow through slit channel with different zeta potentials of the walls. Microfluid. Nanofluid. 15, 35–47.CrossRefGoogle Scholar
Supplementary material: File

Arcos et al. supplementary material

Arcos et al. supplementary material 1

Download Arcos et al. supplementary material(File)
File 87.5 KB