Published online by Cambridge University Press: 08 November 2011
Here we explore the effect of a series of low-permeability tilted baffles on the ascent of a buoyant fluid injected into a porous rock from a linear well, motivated by several industrial processes, particularly CO2 sequestration. We first consider, both theoretically and experimentally, the dynamics associated with flow past an individual inclined baffle; if the incident flux is sufficiently large then a pool of injectate grows beneath the baffle and spills over both ends, partitioning the flux, but otherwise the injectate only flows over the updip end of the baffle, leaving a stagnant zone under the downdip part of the baffle. In a multi-layered system, the flow may then be described using nonlinear recurrence relations based on the flow past an individual baffle. Using this approach, in the particular case in which there is a regular distribution of baffles, we show that, on a scale greater than individual baffles, the flow adjusts to a plume of constant width rising at an angle 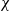 to the vertical, which depends on the geometry of the baffles. This constant-width plume may be described by an effective directional permeability
to the vertical, which depends on the geometry of the baffles. This constant-width plume may be described by an effective directional permeability 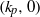 at angles
at angles 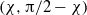 to the vertical where we find
to the vertical where we find 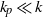 , where
, where 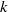 is the effective permeability of the regions between baffles. Within the boundaries of this plume the majority of pore space is bypassed. Indeed, the plume-scale effective porosity is largely associated with the pools of injectate which collect beneath each baffle. We show that since the constant-width plume has such a large lateral extent, the total pore space occupied by the plume, per unit height, is larger than for a homogeneous formation. Furthermore, these pools lead to a large surface area between injectate and formation water, which enhances the reaction of the injectate with the formation water. However, we also show that, in steady state, it may be hard to determine this plume-scale effective porosity since the ratio of the effective Darcy speed and the effective interstitial speed of the plume only relates to the porosity of the updip part of these pools, in which the injectate is flowing.
is the effective permeability of the regions between baffles. Within the boundaries of this plume the majority of pore space is bypassed. Indeed, the plume-scale effective porosity is largely associated with the pools of injectate which collect beneath each baffle. We show that since the constant-width plume has such a large lateral extent, the total pore space occupied by the plume, per unit height, is larger than for a homogeneous formation. Furthermore, these pools lead to a large surface area between injectate and formation water, which enhances the reaction of the injectate with the formation water. However, we also show that, in steady state, it may be hard to determine this plume-scale effective porosity since the ratio of the effective Darcy speed and the effective interstitial speed of the plume only relates to the porosity of the updip part of these pools, in which the injectate is flowing.