Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-25T21:55:18.907Z Has data issue: false hasContentIssue false
  • English
  • Français

Disentangling the origins of torque enhancement through wall roughness in Taylor–Couette turbulence

Published online by Cambridge University Press:  22 December 2016

Xiaojue Zhu ,
Roberto Verzicco  and
Detlef Lohse
Xiaojue Zhu*
Affiliation:
Physics of Fluids Group, MESA+ Institute and J. M. Burgers Centre for Fluid Dynamics, University of Twente, P.O. Box 217, 7500AE Enschede, The Netherlands
Roberto Verzicco
Affiliation:
Physics of Fluids Group, MESA+ Institute and J. M. Burgers Centre for Fluid Dynamics, University of Twente, P.O. Box 217, 7500AE Enschede, The Netherlands Dipartimento di Ingegneria Industriale, University of Rome ‘Tor Vergata’, Via del Politecnico 1, Roma 00133, Italy
Detlef Lohse
Affiliation:
Physics of Fluids Group, MESA+ Institute and J. M. Burgers Centre for Fluid Dynamics, University of Twente, P.O. Box 217, 7500AE Enschede, The Netherlands Max Planck Institute for Dynamics and Self-Organization, 37077 Göttingen, Germany
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Direct numerical simulations (DNS) are performed to analyse the global transport properties of turbulent Taylor–Couette flow with inner rough wall up to Taylor number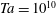$Ta=10^{10}$. The dimensionless torque 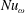$Nu_{\unicode[STIX]{x1D714}}$ shows an effective scaling of 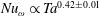$Nu_{\unicode[STIX]{x1D714}}\propto Ta^{0.42\pm 0.01}$, which is steeper than the ultimate regime effective scaling 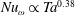$Nu_{\unicode[STIX]{x1D714}}\propto Ta^{0.38}$ seen for smooth inner and outer walls. It is found that at the inner rough wall, the dominant contribution to the torque comes from the pressure forces on the radial faces of the rough elements; while viscous shear stresses on the rough surfaces contribute little to 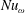$Nu_{\unicode[STIX]{x1D714}}$. Thus, the log layer close to the rough wall depends on the roughness length scale, rather than on the viscous length scale. We then separate the torque contributed from the smooth inner wall and the rough outer wall. It is found that the smooth wall torque scaling follows 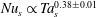$Nu_{s}\propto Ta_{s}^{0.38\pm 0.01}$, in excellent agreement with the case where both walls are smooth. In contrast, the rough wall torque scaling follows 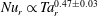$Nu_{r}\propto Ta_{r}^{0.47\pm 0.03}$, very close to the pure ultimate regime scaling 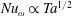$Nu_{\unicode[STIX]{x1D714}}\propto Ta^{1/2}$. The energy dissipation rate at the wall of an inner rough cylinder decreases significantly as a consequence of the wall shear stress reduction caused by the flow separation at the rough elements. On the other hand, the latter shed vortices in the bulk that are transported towards the outer cylinder and dissipated. Compared to the purely smooth case, the inner wall roughness renders the system more bulk dominated and thus increases the effective scaling exponent.

JFM classification

Convection: Plumes/thermals Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 812 , 10 February 2017 , pp. 279 - 293
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503–537.Google Scholar
van den Berg, T., Doering, C., Lohse, D. & Lathrop, D. 2003 Smooth and rough boundaries in turbulent Taylor–Couette flow. Phys. Rev. E 68, 036307.Google ScholarPubMed
Brauckmann, H. J. & Eckhardt, B. 2013 Direct numerical simulations of local and global torque in Taylor–Couette flow up to Re = 30 000. J. Fluid Mech. 718, 398–427.CrossRefGoogle Scholar
Busse, F. 2012 Viewpoint: the twins of turbulence research. Physics 5, 4.Google Scholar
Cadot, O., Couder, Y., Daerr, A., Douady, S. & Tsinober, A. 1997 Energy injection in closed turbulent flows: stirring through boundary layers versus inertial stirring. Phys. Rev. E 56, 427–433.Google Scholar
Ciliberto, S. & Laroche, C. 1999 Random roughness of boundary increases the turbulent scaling exponents. Phys. Rev. Lett. 82, 3998–4001.Google Scholar
Du, Y.-B. & Tong, P. 2000 Turbulent thermal convection in a cell with ordered rough boundaries. J. Fluid Mech. 407, 57–84.CrossRefGoogle Scholar
Eckhardt, B., Grossmann, S. & Lohse, D. 2007a Fluxes and energy dissipation in thermal convection and shear flows. Europhys. Lett. 78, 24001.Google Scholar
Eckhardt, B., Grossmann, S. & Lohse, D. 2007b Torque scaling in turbulent Taylor–Couette flow between independently rotating cylinders. J. Fluid Mech. 581, 221–250.Google Scholar
Fadlun, E. A., Verzicco, R., Orlandi, P. & Mohd-Yusof, J. 2000 Combined immersed-boundary finite-difference methods for three-dimensional complex flow simulations. J. Comput. Phys. 161, 35–60.CrossRefGoogle Scholar
van Gils, D. P. M., Huisman, S. G., Bruggert, G.-W., Sun, C. & Lohse, D. 2011 Torque scaling in turbulent Taylor–Couette flow with co- and counterrotating cylinders. Phys. Rev. Lett. 106, 024502.Google Scholar
Grossmann, S. & Lohse, D. 2000 Scaling in thermal convection: a unifying theory. J. Fluid Mech. 407, 27–56.CrossRefGoogle Scholar
Grossmann, S. & Lohse, D. 2001 Thermal convection for large Prandtl numbers. Phys. Rev. Lett. 86, 3316–3319.CrossRefGoogle ScholarPubMed
Grossmann, S. & Lohse, D. 2004 Fluctuations in turbulent Rayleigh–Bénard convection: the role of plumes. Phys. Fluids 16 (12), 4462.Google Scholar
Grossmann, S. & Lohse, D. 2011 Multiple scaling in the ultimate regime of thermal convection. Phys. Fluids 23, 045108.CrossRefGoogle Scholar
Grossmann, S., Lohse, D. & Sun, C. 2014 Velocity profiles in strongly turbulent Taylor–Couette flow. Phys. Fluids 26 (2), 025114.CrossRefGoogle Scholar
Grossmann, S., Lohse, D. & Sun, C. 2016 High-Reynolds number Taylor–Couette turbulence. Annu. Rev. Fluid Mech. 48, 53–80.CrossRefGoogle Scholar
He, X., Funfschilling, D., Bodenschatz, E. & Ahlers, G. 2012a Heat transport by turbulent Rayleigh–Bénard convection for Pr ≃ 0. 8 and 4 × 1011 ≲ Ra ≲ 2 × 1014 : ultimate-state transition for aspect ratio 𝛤 = 1. 00. New J. Phys. 14, 063030.Google Scholar
He, X., Funfschilling, D., Nobach, H., Bodenschatz, E. & Ahlers, G. 2012b Transition to the ultimate state of turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 108, 024502.CrossRefGoogle Scholar
Huisman, S. G., van Gils, D. P. M., Grossmann, S., Sun, C. & Lohse, D. 2012 Ultimate turbulent Taylor–Couette flow. Phys. Rev. Lett. 108, 024501.CrossRefGoogle ScholarPubMed
Huisman, S. G., Scharnowski, S., Cierpka, C., Kähler, C. J., Lohse, D. & Sun, C. 2013 Logarithmic boundary layers in strong Taylor–Couette turbulence. Phys. Rev. Lett. 110, 264501.Google Scholar
Ikeda, T. & Durbin, P. A. 2007 Direct simulations of a rough-wall channel flow. J. Fluid Mech. 571, 235–263.CrossRefGoogle Scholar
Kraichnan, R. H. 1962 Turbulent thermal convection at arbritrary Prandtl number. Phys. Fluids 5, 1374–1389.Google Scholar
Lathrop, D. P., Fineberg, J. & Swinney, H. L. 1992 Turbulent flow between concentric rotating cylinders at large Reynolds number. Phys. Rev. Lett. 68, 1515–1518.CrossRefGoogle ScholarPubMed
Lewis, G. S. & Swinney, H. L. 1999 Velocity structure functions, scaling, and transitions in high-Reynolds-number Couette–Taylor flow. Phys. Rev. E 59, 5457–5467.Google ScholarPubMed
McKeon, B. J., Zagarola, M. V. & Smits, A. J. 2005 A new friction factor relationship for fully developed pipe flow. J. Fluid Mech. 538, 429–443.CrossRefGoogle Scholar
Nikuradse, J. 1933 Strömungsgesetze in rauhen Rohren. Forschungsheft Arb. Ing.-Wes. 361.Google Scholar
Ostilla-Mónico, R., van der Poel, E. P., Verzicco, R., Grossmann, S. & Lohse, D. 2014a Boundary layer dynamics at the transition between the classical and the ultimate regime of Taylor–Couette flow. Phys. Fluids 26, 015114.Google Scholar
Ostilla-Mónico, R., van der Poel, E. P., Verzicco, R., Grossmann, S. & Lohse, D. 2014b Phase diagram of turbulent Taylor–Couette flow. J. Fluid Mech. 761, 1–26.Google Scholar
Ostilla, R., Stevens, R. J. A. M., Grossmann, S., Verzicco, R. & Lohse, D. 2013 Optimal Taylor–Couette flow: direct numerical simulations. J. Fluid Mech. 719, 14–46.Google Scholar
Ostilla-Mónico, R., Verzicco, R., Grossmann, S. & Lohse, D. 2016 The near-wall region of highly turbulent Taylor–Couette flow. J. Fluid Mech. 788, 95–117.CrossRefGoogle Scholar
van der Poel, E. P., Ostilla-Mónico, R., Donners, J. & Verzicco, R. 2015 A pencil distributed code for simulating wall-bounded turbulent convection. Comput. Fluids 116, 10–16.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Roche, P.-E., Castaing, B., Chabaud, B. & Hébral, B. 2001 Observation of the 1/2 power law in Rayleigh–Bénard convection. Phys. Rev. E 63, 045303(R).Google Scholar
Schlichting, H. 1979 Boundary Layer Theory, 7th edn. McGraw-Hill.Google Scholar
Shen, Y., Tong, P. & Xia, K.-Q. 1996 Turbulent convection over rough surfaces. Phys. Rev. Lett. 76, 908–911.Google Scholar
Stringano, G., Pascazio, G. & Verzicco, R. 2006 Turbulent thermal convection over grooved plates. J. Fluid Mech. 557, 307–336.Google Scholar
Tisserand, J. C., Creyssels, M., Gasteuil, Y., Pabiou, H., Gibert, M., Castaing, B. & Chillà, F. 2011 Comparison between rough and smooth plates within the same Rayleigh–Bénard cell. Phys. Fluids 23, 015105.CrossRefGoogle Scholar
Verzicco, R. & Orlandi, P. 1996 A finite-difference scheme for three-dimensional incompressible flows in cylindrical coordinates. J. Comput. Phys. 123, 402–413.Google Scholar
Wagner, S. & Shishkina, O. 2014 Heat flux enhancement by regular surface roughness in turbulent thermal convection. J. Fluid Mech. 763, 109–135.Google Scholar
Wei, P., Chan, T.-S., Ni, R., Zhao, X.-Z. & Xia, K.-Q. 2014 Heat transport properties of plates with smooth and rough surfaces in turbulent thermal convection. J. Fluid Mech. 740, 28–46.Google Scholar
Zanoun, E.-S., Nagib, H. & Durst, F. 2009 Refined c f relation for turbulent channels and consequences for high-Re experiments. Fluid Dyn. Res. 41 (2), 021405.Google Scholar