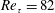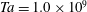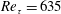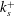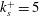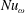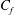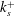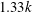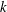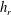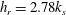1 Introduction
Many turbulent flows in nature and industry are bounded by rough boundaries. Examples are the surface of planet Earth with respect to geophysical flows or fouling on ship hulls with respect to open waters. Such rough boundaries strongly influence the total drag, with often adverse consequences in the form of higher transport costs. Therefore, it becomes of paramount importance to understand the physics behind such changes in drag, ultimately leading to better informed management of the problem. One key recurring question concerns the influence of the roughness topology on the drag coefficient.
Seminal work by Nikuradse (Reference Nikuradse1933) investigated the influence of the height of closely packed, monodisperse, sand grains in pipe flow. This work has become one of the pillars in the field. Later, a vast amount of research was carried out to study the influence of roughness on the canonical systems of turbulence – pipe, channel and boundary layer flows – aiming for a better understanding of the roughness effects on turbulent flows Ligrani & Moffat (Reference Ligrani and Moffat1986), Schultz & Flack (Reference Schultz and Flack2007), Chan et al. (Reference Chan, MacDonald, Chung, Hutchins and Ooi2015), Busse, Thakkar & Sandham (Reference Busse, Thakkar and Sandham2017); also see Jiménez (Reference Jiménez2004) and Schultz & Flack (Reference Schultz and Flack2010) for comprehensive reviews.
Next to pipe flow, Taylor–Couette (TC) flow – the flow between two coaxial, independently rotating cylinders – is another canonical system in turbulence (Grossmann, Lohse & Sun Reference Grossmann, Lohse and Sun2016). Closely related to its ‘twin’ of Rayleigh–Bénard (RB) turbulence (Busse Reference Busse2012; Eckhardt, Grossmann & Lohse Reference Eckhardt, Grossmann and Lohse2007), it serves as an ideal system to study the interaction between boundary layer and bulk flow. Very long spatial transients, as found in open systems, are bypassed by the circumferential restrictions. Since the domain is closed, global balances can easily be derived and monitored, giving room for extensive comparison between theory, experiments and simulations. Further, the streamwise curvature effects find many applications in industry. For these reasons, we set out to investigate the effects of roughness on the turbulent fluid flow in the TC system.
Over the last century, much work has been carried out with the aim of understanding the effect of the roughness topology on fluid flow. One of the consequences of roughness is the change of the wall drag, which can be expressed as a shift of the mean streamwise velocity profile
![]() $\unicode[STIX]{x0394}u^{+}\equiv (u_{s}-u_{r})/u_{\unicode[STIX]{x1D70F}}$
, where
$\unicode[STIX]{x0394}u^{+}\equiv (u_{s}-u_{r})/u_{\unicode[STIX]{x1D70F}}$
, where
![]() $\unicode[STIX]{x0394}u^{+}$
is known as the Hama roughness function (Hama Reference Hama1954) and
$\unicode[STIX]{x0394}u^{+}$
is known as the Hama roughness function (Hama Reference Hama1954) and
![]() $u_{s},u_{r}$
are the smooth-wall and the rough-wall mean streamwise velocities, respectively. Clauser (Reference Clauser1954) and Hama (Reference Hama1954) observed that roughness effects are confined to the inner region of the boundary layer. This idea was postulated by Townsend (Reference Townsend1956), who referred to it as Reynolds number similarity. The hypothesis states that outside the roughness sublayer, the structure of the flow is independent of the wall roughness, except for the role of the wall in setting the wall stress
$u_{s},u_{r}$
are the smooth-wall and the rough-wall mean streamwise velocities, respectively. Clauser (Reference Clauser1954) and Hama (Reference Hama1954) observed that roughness effects are confined to the inner region of the boundary layer. This idea was postulated by Townsend (Reference Townsend1956), who referred to it as Reynolds number similarity. The hypothesis states that outside the roughness sublayer, the structure of the flow is independent of the wall roughness, except for the role of the wall in setting the wall stress
![]() $\unicode[STIX]{x1D70F}_{w}$
. The hypothesis, now known as Townsend’s outer layer similarity, has found strong support over time (Raupach, Antonia & Rajagopalan Reference Raupach, Antonia and Rajagopalan1991; Flack & Schultz Reference Flack and Schultz2014). The logarithmic region is thus dynamically not influenced by the roughness and the mean streamwise velocity profile
$\unicode[STIX]{x1D70F}_{w}$
. The hypothesis, now known as Townsend’s outer layer similarity, has found strong support over time (Raupach, Antonia & Rajagopalan Reference Raupach, Antonia and Rajagopalan1991; Flack & Schultz Reference Flack and Schultz2014). The logarithmic region is thus dynamically not influenced by the roughness and the mean streamwise velocity profile
![]() $u(y)$
there becomes (Pope Reference Pope2000)
$u(y)$
there becomes (Pope Reference Pope2000)
As usual, the superscript ‘
![]() $+$
’ indicates a scaling in viscous units (i.e. length
$+$
’ indicates a scaling in viscous units (i.e. length
![]() $y^{+}=yu_{\unicode[STIX]{x1D70F}}/\unicode[STIX]{x1D708}$
and velocity
$y^{+}=yu_{\unicode[STIX]{x1D70F}}/\unicode[STIX]{x1D708}$
and velocity
![]() $u^{+}=u/u_{\unicode[STIX]{x1D70F}}$
) and
$u^{+}=u/u_{\unicode[STIX]{x1D70F}}$
) and
![]() $u_{\unicode[STIX]{x1D70F}}$
is the friction velocity,
$u_{\unicode[STIX]{x1D70F}}$
is the friction velocity,
![]() $u_{\unicode[STIX]{x1D70F}}=\sqrt[]{\unicode[STIX]{x1D70F}_{w}/\unicode[STIX]{x1D70C}}$
with
$u_{\unicode[STIX]{x1D70F}}=\sqrt[]{\unicode[STIX]{x1D70F}_{w}/\unicode[STIX]{x1D70C}}$
with
![]() $\unicode[STIX]{x1D70F}_{w}$
being the total stress at the wall, and
$\unicode[STIX]{x1D70F}_{w}$
being the total stress at the wall, and
![]() $\unicode[STIX]{x1D70C}$
the fluid density. We calculate
$\unicode[STIX]{x1D70C}$
the fluid density. We calculate
![]() $\unicode[STIX]{x1D70F}_{w}$
at the outer wall, which is smooth. Because the torque is the same on both cylinders, we can calculate the wall shear stress on the inner cylinder by
$\unicode[STIX]{x1D70F}_{w}$
at the outer wall, which is smooth. Because the torque is the same on both cylinders, we can calculate the wall shear stress on the inner cylinder by
![]() $\unicode[STIX]{x1D70F}_{w,i}=\unicode[STIX]{x1D70F}_{w,o}/\unicode[STIX]{x1D702}^{2}$
, where
$\unicode[STIX]{x1D70F}_{w,i}=\unicode[STIX]{x1D70F}_{w,o}/\unicode[STIX]{x1D702}^{2}$
, where
![]() $\unicode[STIX]{x1D702}$
is the radius ratio. Note that in this representation, the skin-friction coefficient
$\unicode[STIX]{x1D702}$
is the radius ratio. Note that in this representation, the skin-friction coefficient
![]() $C_{f}$
is related to the friction velocity by
$C_{f}$
is related to the friction velocity by
![]() $C_{f}=2(u_{\unicode[STIX]{x1D70F}}/U_{0})^{2}$
, where
$C_{f}=2(u_{\unicode[STIX]{x1D70F}}/U_{0})^{2}$
, where
![]() $U_{0}$
is the centreline velocity (Pope Reference Pope2000). It has been found that for TC turbulence
$U_{0}$
is the centreline velocity (Pope Reference Pope2000). It has been found that for TC turbulence
![]() $\unicode[STIX]{x1D705}$
and
$\unicode[STIX]{x1D705}$
and
![]() $A$
are not constant anymore, but are functions of the inner cylinder Reynolds number
$A$
are not constant anymore, but are functions of the inner cylinder Reynolds number
![]() $Re_{i}$
at least until
$Re_{i}$
at least until
![]() $Re_{i}=10^{6}$
(Huisman et al.
Reference Huisman, Scharnowski, Cierpka, Kähler, Lohse and Sun2013). Therefore, for TC we here suggest the generalization,
$Re_{i}=10^{6}$
(Huisman et al.
Reference Huisman, Scharnowski, Cierpka, Kähler, Lohse and Sun2013). Therefore, for TC we here suggest the generalization,
with
![]() $f_{1}(Re_{i})$
and
$f_{1}(Re_{i})$
and
![]() $f_{2}(Re_{i})$
being unknown functions. The questions now are: (i) How does
$f_{2}(Re_{i})$
being unknown functions. The questions now are: (i) How does
![]() $\unicode[STIX]{x0394}u^{+}$
depend on the parameters that characterize the surface geometry; and (ii) Can
$\unicode[STIX]{x0394}u^{+}$
depend on the parameters that characterize the surface geometry; and (ii) Can
![]() $\unicode[STIX]{x0394}u^{+}$
be generalized to other flows?
$\unicode[STIX]{x0394}u^{+}$
be generalized to other flows?
Although many parameters influence the Hama roughness function
![]() $\unicode[STIX]{x0394}u^{+}$
(Schlichting Reference Schlichting1936; Musker Reference Musker1980; Napoli, Armenio & De Marchis Reference Napoli, Armenio and De Marchis2008; Chan et al.
Reference Chan, MacDonald, Chung, Hutchins and Ooi2015; MacDonald et al.
Reference MacDonald, Chan, Chung, Hutchins and Ooi2016), the most relevant parameter is the characteristic height of the roughness
$\unicode[STIX]{x0394}u^{+}$
(Schlichting Reference Schlichting1936; Musker Reference Musker1980; Napoli, Armenio & De Marchis Reference Napoli, Armenio and De Marchis2008; Chan et al.
Reference Chan, MacDonald, Chung, Hutchins and Ooi2015; MacDonald et al.
Reference MacDonald, Chan, Chung, Hutchins and Ooi2016), the most relevant parameter is the characteristic height of the roughness
![]() $k^{+}$
. In a regime in which the pressure forces dominate the drag force, any surface can be collapsed onto the Nikuradse data by rescaling the roughness height to the so-called ‘equivalent sand grain roughness height’
$k^{+}$
. In a regime in which the pressure forces dominate the drag force, any surface can be collapsed onto the Nikuradse data by rescaling the roughness height to the so-called ‘equivalent sand grain roughness height’
![]() $k_{s}^{+}$
. Nikuradse (Reference Nikuradse1933) found that three regimes of the characteristic roughness height
$k_{s}^{+}$
. Nikuradse (Reference Nikuradse1933) found that three regimes of the characteristic roughness height
![]() $k_{s}^{+}$
can be identified with respect to the effect of roughness (Flack, Schultz & Rose Reference Flack, Schultz and Rose2012). For
$k_{s}^{+}$
can be identified with respect to the effect of roughness (Flack, Schultz & Rose Reference Flack, Schultz and Rose2012). For
![]() $k_{s}^{+}\lesssim 5$
, the rough wall appears to be hydrodynamically smooth and the roughness function
$k_{s}^{+}\lesssim 5$
, the rough wall appears to be hydrodynamically smooth and the roughness function
![]() $\unicode[STIX]{x0394}u^{+}$
goes to zero. For
$\unicode[STIX]{x0394}u^{+}$
goes to zero. For
![]() $k_{s}^{+}\gtrsim 70$
, the wall drag scales quadratically with the fluid velocity and the friction factor
$k_{s}^{+}\gtrsim 70$
, the wall drag scales quadratically with the fluid velocity and the friction factor
![]() $C_{f}$
is independent of the Reynolds number, indicating that hydrodynamic pressure drag (also called form drag) on the roughness dominates the total drag. The transitionally rough regime is in between these two regimes. Where in the fully rough regime, a surface is fully determined by
$C_{f}$
is independent of the Reynolds number, indicating that hydrodynamic pressure drag (also called form drag) on the roughness dominates the total drag. The transitionally rough regime is in between these two regimes. Where in the fully rough regime, a surface is fully determined by
![]() $k_{s}^{+}$
to give a collapse onto the fully rough asymptote (Schultz & Flack Reference Schultz and Flack2010), in the transitionally rough regime, different surfaces give rise to different roughness functions, see e.g. figure 3 in Jiménez (Reference Jiménez2004). This can be attributed to the delicate interplay between pressure drag, viscous drag and the weakening of the so-called turbulence generation cycle (Jiménez Reference Jiménez2004).
$k_{s}^{+}$
to give a collapse onto the fully rough asymptote (Schultz & Flack Reference Schultz and Flack2010), in the transitionally rough regime, different surfaces give rise to different roughness functions, see e.g. figure 3 in Jiménez (Reference Jiménez2004). This can be attributed to the delicate interplay between pressure drag, viscous drag and the weakening of the so-called turbulence generation cycle (Jiménez Reference Jiménez2004).
An intriguing feature of the data from Nikuradse (Reference Nikuradse1933) is at
![]() $k_{s}^{+}\approx 5$
, where roughness effects suddenly result in an inflectional increase of
$k_{s}^{+}\approx 5$
, where roughness effects suddenly result in an inflectional increase of
![]() $\unicode[STIX]{x0394}u^{+}$
, as compared to the gradual increase of the roughness function found by Colebrook (Reference Colebrook1939) who extracted an empirical relationship from many industrial surfaces (Shockling, Allen & Smits Reference Shockling, Allen and Smits2006). Later, this inflectional behaviour was also observed for tightly packed spheres (Ligrani & Moffat Reference Ligrani and Moffat1986), honed surfaces (Shockling et al.
Reference Shockling, Allen and Smits2006) and grit-blasted surfaces (Thakkar, Busse & Sandham Reference Thakkar, Busse and Sandham2018). Chan-Braun, Garcia-Villalba & Uhlmann (Reference Chan-Braun, Garcia-Villalba and Uhlmann2011) had too few points to find the inflectional behaviour; however, their two simulations of monodisperse spheres in regular arrangement collapsed onto the Nikuradse curve. In the Moody (Reference Moody1944) representation, this inflectional behaviour manifests itself as a dip in the friction factor
$\unicode[STIX]{x0394}u^{+}$
, as compared to the gradual increase of the roughness function found by Colebrook (Reference Colebrook1939) who extracted an empirical relationship from many industrial surfaces (Shockling, Allen & Smits Reference Shockling, Allen and Smits2006). Later, this inflectional behaviour was also observed for tightly packed spheres (Ligrani & Moffat Reference Ligrani and Moffat1986), honed surfaces (Shockling et al.
Reference Shockling, Allen and Smits2006) and grit-blasted surfaces (Thakkar, Busse & Sandham Reference Thakkar, Busse and Sandham2018). Chan-Braun, Garcia-Villalba & Uhlmann (Reference Chan-Braun, Garcia-Villalba and Uhlmann2011) had too few points to find the inflectional behaviour; however, their two simulations of monodisperse spheres in regular arrangement collapsed onto the Nikuradse curve. In the Moody (Reference Moody1944) representation, this inflectional behaviour manifests itself as a dip in the friction factor
![]() $C_{f}$
, leading to a significantly lower drag coefficient (
$C_{f}$
, leading to a significantly lower drag coefficient (
![]() ${\approx}20\,\%$
(Bradshaw Reference Bradshaw2000)) in comparison to the monotonic behaviour of Colebrook (Reference Colebrook1939), on which the original Moody diagram is based. Although it is proposed that the inflectional behaviour has to do with the monodispersity of the roughness leading to a critical Reynolds number at which the elements become active (Jiménez Reference Jiménez2004), recent simulations by Thakkar et al. (Reference Thakkar, Busse and Sandham2018) for a polydisperse surface (containing irregularities with a range of sizes) also show this inflectional behaviour. In a broader sense, the direct numerical simulations (DNSs) by Thakkar et al. (Reference Thakkar, Busse and Sandham2018) are interesting since they show, for the first time, a surface that very closely resembles the Nikuradse (Reference Nikuradse1933) roughness function in all regimes; the authors found
${\approx}20\,\%$
(Bradshaw Reference Bradshaw2000)) in comparison to the monotonic behaviour of Colebrook (Reference Colebrook1939), on which the original Moody diagram is based. Although it is proposed that the inflectional behaviour has to do with the monodispersity of the roughness leading to a critical Reynolds number at which the elements become active (Jiménez Reference Jiménez2004), recent simulations by Thakkar et al. (Reference Thakkar, Busse and Sandham2018) for a polydisperse surface (containing irregularities with a range of sizes) also show this inflectional behaviour. In a broader sense, the direct numerical simulations (DNSs) by Thakkar et al. (Reference Thakkar, Busse and Sandham2018) are interesting since they show, for the first time, a surface that very closely resembles the Nikuradse (Reference Nikuradse1933) roughness function in all regimes; the authors found
![]() $k_{s}^{+}=0.87k_{t}^{+}$
, where
$k_{s}^{+}=0.87k_{t}^{+}$
, where
![]() $k_{t}$
is the mean peak-to-valley height.
$k_{t}$
is the mean peak-to-valley height.
Regarding TC flow, only a few studies have looked at the effect of roughness (Cadot et al.
Reference Cadot, Couder, Daerr, Douady and Tsinober1997; van den Berg et al.
Reference van den Berg, Doering, Lohse and Lathrop2003). Recently, the effect of regular roughness on TC turbulence has also been investigated by means of DNS (Zhu et al.
Reference Zhu, Ostilla-Mónico, Verzicco and Lohse2016; Zhu, Verzicco & Lohse Reference Zhu, Verzicco and Lohse2017; Zhu et al.
Reference Zhu, Verschoof, Bakhuis, Huisman, Verzicco, Sun and Lohse2018b
). Zhu et al. (Reference Zhu, Ostilla-Mónico, Verzicco and Lohse2016) looked at the effect of axisymmetric grooves on the torque scaling, boundary layer thickness and plume ejections. They find that enhanced plume ejection from the roughness tips can lead to an ultimate torque scaling exponent of
![]() $Nu\propto Ta^{0.5}$
, although for higher
$Nu\propto Ta^{0.5}$
, although for higher
![]() $Ta$
the exponent saturates back to the ultimate scaling effective exponent of 0.38. Zhu et al. (Reference Zhu, Verzicco and Lohse2017) then simulate transverse bar roughness elements on the inner cylinder to disentangle the separate effects of viscosity and pressure, and find that the ultimate torque scaling exponent of
$Ta$
the exponent saturates back to the ultimate scaling effective exponent of 0.38. Zhu et al. (Reference Zhu, Verzicco and Lohse2017) then simulate transverse bar roughness elements on the inner cylinder to disentangle the separate effects of viscosity and pressure, and find that the ultimate torque scaling exponent of
![]() $Nu\propto Ta^{0.5}$
is only possible when the pressure forces dominate at the rough boundary (Zhu et al.
Reference Zhu, Verschoof, Bakhuis, Huisman, Verzicco, Sun and Lohse2018b
).
$Nu\propto Ta^{0.5}$
is only possible when the pressure forces dominate at the rough boundary (Zhu et al.
Reference Zhu, Verschoof, Bakhuis, Huisman, Verzicco, Sun and Lohse2018b
).
In contrast to the above mentioned previous work, in which the roughness consisted of well-defined transverse bars with constant distance and heights (Zhu et al.
Reference Zhu, Verzicco and Lohse2017, Reference Zhu, Verschoof, Bakhuis, Huisman, Verzicco, Sun and Lohse2018b
), in this research we set out to investigate the effects of irregular, monodisperse roughness, resembling the sand grain roughness reported by Nikuradse (Reference Nikuradse1933). We model the roughness as randomly rotated and semi-randomly translated ellipsoids of constant volume and aspect ratio, based on the roughness model (subgrid scale) of Scotti (Reference Scotti2006). Previously, a fully resolved version of the model by Scotti (Reference Scotti2006) was used for large-eddy simulations in channel flow (Yuan & Piomelli Reference Yuan and Piomelli2014). Taylor numbers in our DNS range from
![]() $Ta=1.0\times 10^{7}$
(
$Ta=1.0\times 10^{7}$
(
![]() $Re_{\unicode[STIX]{x1D70F}}=82$
) to
$Re_{\unicode[STIX]{x1D70F}}=82$
) to
![]() $Ta=1.0\times 10^{9}$
(
$Ta=1.0\times 10^{9}$
(
![]() $Re_{\unicode[STIX]{x1D70F}}=635$
); therefore, we capture both classical (laminar-like boundary layers) and ultimate (turbulent boundary layers) regimes (Ostilla-Mónico et al.
Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014; Grossmann et al.
Reference Grossmann, Lohse and Sun2016; Zhu et al.
Reference Zhu, Verschoof, Bakhuis, Huisman, Verzicco, Sun and Lohse2018b
). Moreover, whereas previous research on roughness in TC flow focussed on the torque scaling, we now look at the effects of the roughness height on the Hama roughness function
$Re_{\unicode[STIX]{x1D70F}}=635$
); therefore, we capture both classical (laminar-like boundary layers) and ultimate (turbulent boundary layers) regimes (Ostilla-Mónico et al.
Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014; Grossmann et al.
Reference Grossmann, Lohse and Sun2016; Zhu et al.
Reference Zhu, Verschoof, Bakhuis, Huisman, Verzicco, Sun and Lohse2018b
). Moreover, whereas previous research on roughness in TC flow focussed on the torque scaling, we now look at the effects of the roughness height on the Hama roughness function
![]() $\unicode[STIX]{x0394}u^{+}$
in the transitionally rough and fully rough regimes, ranging from
$\unicode[STIX]{x0394}u^{+}$
in the transitionally rough and fully rough regimes, ranging from
![]() $k_{s}^{+}=5$
to
$k_{s}^{+}=5$
to
![]() $k_{s}^{+}=92$
.
$k_{s}^{+}=92$
.
This manuscript is structured as follows. In §§ 2 and 3, we elaborate on the TC set-up, the roughness model and the numerical procedure. In § 4.1, we study the velocity profiles and present the effects of the roughness height on the Hama roughness function. In § 4.2, we present the global response of the system. In § 4.3 we study the flow structures. In § 4.4 the fluctuations close to the roughness are studied and in § 4.5 we present radial profiles of various other quantities. Finally, in § 5 we draw our conclusions and propose future research directions.
2 Taylor–Couette flow

Figure 1. Illustration of the Taylor–Couette (TC) set-up. (a) TC set-up with inner cylinder sand grain roughness:
![]() $\unicode[STIX]{x1D714}_{i}$
is the inner cylinder angular velocity,
$\unicode[STIX]{x1D714}_{i}$
is the inner cylinder angular velocity,
![]() $r_{i}$
is the inner cylinder radius,
$r_{i}$
is the inner cylinder radius,
![]() $r_{o}$
is the outer cylinder radius and
$r_{o}$
is the outer cylinder radius and
![]() $d=r_{o}-r_{i}$
the gap width. (b) A zoom of the sand grain roughness that is modelled. The outer cylinder is stationary and smooth.
$d=r_{o}-r_{i}$
the gap width. (b) A zoom of the sand grain roughness that is modelled. The outer cylinder is stationary and smooth.
The TC set-up, as shown in figure 1, comprises independently co- or counter-rotating concentric cylinders around their vertical axes. The flow, driven by the shear on both of the cylinders, fills the gap between the cylinders;
![]() $r_{i}$
is the inner cylinder radius,
$r_{i}$
is the inner cylinder radius,
![]() $r_{o}$
is the outer cylinder radius and the radius ratio is defined as
$r_{o}$
is the outer cylinder radius and the radius ratio is defined as
![]() $\unicode[STIX]{x1D702}=r_{i}/r_{o}$
. For this research, we set
$\unicode[STIX]{x1D702}=r_{i}/r_{o}$
. For this research, we set
![]() $\unicode[STIX]{x1D702}\approx 0.714$
, to match the experimental T
$\unicode[STIX]{x1D702}\approx 0.714$
, to match the experimental T
![]() $^{3}$
C set-up (Huisman et al.
Reference Huisman, Scharnowski, Cierpka, Kähler, Lohse and Sun2013), and previous simulations (Zhu et al.
Reference Zhu, Verzicco and Lohse2017).
$^{3}$
C set-up (Huisman et al.
Reference Huisman, Scharnowski, Cierpka, Kähler, Lohse and Sun2013), and previous simulations (Zhu et al.
Reference Zhu, Verzicco and Lohse2017).
![]() $\unicode[STIX]{x1D6E4}=L/d$
is the aspect ratio, where
$\unicode[STIX]{x1D6E4}=L/d$
is the aspect ratio, where
![]() $L$
is the height of the cylinders, and
$L$
is the height of the cylinders, and
![]() $d=r_{o}-r_{i}=0.4r_{i}$
is the gap width. Here,
$d=r_{o}-r_{i}=0.4r_{i}$
is the gap width. Here,
![]() $\unicode[STIX]{x1D6E4}\approx 2$
such that one pair of Taylor vortices fits in the gap, and the mean flow statistics become independent of the aspect ratio (Ostilla-Mónico, Verzicco & Lohse Reference Ostilla-Mónico, Verzicco and Lohse2015). In the azimuthal direction we employ a rotational symmetry of order
$\unicode[STIX]{x1D6E4}\approx 2$
such that one pair of Taylor vortices fits in the gap, and the mean flow statistics become independent of the aspect ratio (Ostilla-Mónico, Verzicco & Lohse Reference Ostilla-Mónico, Verzicco and Lohse2015). In the azimuthal direction we employ a rotational symmetry of order
![]() $6$
to save on computational expense such that the streamwise aspect ratio of our simulations becomes
$6$
to save on computational expense such that the streamwise aspect ratio of our simulations becomes
![]() $L_{\unicode[STIX]{x1D703}}/d=(r_{i}2\unicode[STIX]{x03C0}/6)/d=2.62$
. Brauckmann & Eckhardt (Reference Brauckmann and Eckhardt2013) and Ostilla-Mónico et al. (Reference Ostilla-Mónico, Verzicco and Lohse2015) found that this reduction of the streamwise extent does not affect the mean flow statistics. This gives
$L_{\unicode[STIX]{x1D703}}/d=(r_{i}2\unicode[STIX]{x03C0}/6)/d=2.62$
. Brauckmann & Eckhardt (Reference Brauckmann and Eckhardt2013) and Ostilla-Mónico et al. (Reference Ostilla-Mónico, Verzicco and Lohse2015) found that this reduction of the streamwise extent does not affect the mean flow statistics. This gives
![]() $L_{\unicode[STIX]{x1D703}}/(d/2)=5.24$
and
$L_{\unicode[STIX]{x1D703}}/(d/2)=5.24$
and
![]() $L/(d/2)\approx 4.0$
.
$L/(d/2)\approx 4.0$
.
To maintain convenient boundary conditions, we solve the Navier–Stokes (NS) equations in a reference frame rotating with the inner cylinder (
![]() $\unicode[STIX]{x1D714}_{i}\boldsymbol{e}_{z}$
). The NS equations, with
$\unicode[STIX]{x1D714}_{i}\boldsymbol{e}_{z}$
). The NS equations, with
![]() $(u,v,w)$
the (streamwise/azimuthal, spanwise/axial, wall-normal/radial) velocity components respectively, in that reference frame become
$(u,v,w)$
the (streamwise/azimuthal, spanwise/axial, wall-normal/radial) velocity components respectively, in that reference frame become
with no-slip boundary conditions
![]() $u|_{r=r_{i}}=0$
,
$u|_{r=r_{i}}=0$
,
![]() $u|_{r=r_{o}}=r_{o}(\unicode[STIX]{x1D714}_{o}-\unicode[STIX]{x1D714}_{i})$
. Equation (2.4) expresses the incompressible restriction. Hatted symbols indicate the respective dimensionless variables, with
$u|_{r=r_{o}}=r_{o}(\unicode[STIX]{x1D714}_{o}-\unicode[STIX]{x1D714}_{i})$
. Equation (2.4) expresses the incompressible restriction. Hatted symbols indicate the respective dimensionless variables, with
![]() $\boldsymbol{u}=r_{i}|\unicode[STIX]{x1D714}_{i}-\unicode[STIX]{x1D714}_{o}|\hat{\boldsymbol{u}}$
,
$\boldsymbol{u}=r_{i}|\unicode[STIX]{x1D714}_{i}-\unicode[STIX]{x1D714}_{o}|\hat{\boldsymbol{u}}$
,
![]() $r=\text{d}\hat{r}$
and
$r=\text{d}\hat{r}$
and
![]() $t=\text{d}/r_{i}|\unicode[STIX]{x1D714}_{i}-\unicode[STIX]{x1D714}_{o}|\hat{t}$
.
$t=\text{d}/r_{i}|\unicode[STIX]{x1D714}_{i}-\unicode[STIX]{x1D714}_{o}|\hat{t}$
.
![]() $f(\unicode[STIX]{x1D702})/Ta^{1/2}=Re^{-1}$
where
$f(\unicode[STIX]{x1D702})/Ta^{1/2}=Re^{-1}$
where
![]() $f(\unicode[STIX]{x1D702})$
is the so-called ‘geometric Prandtl’ number (Eckhardt et al.
Reference Eckhardt, Grossmann and Lohse2007),
$f(\unicode[STIX]{x1D702})$
is the so-called ‘geometric Prandtl’ number (Eckhardt et al.
Reference Eckhardt, Grossmann and Lohse2007),
here
![]() $f(0.714)\approx 1.23$
.
$f(0.714)\approx 1.23$
.
![]() $Ta$
is the Taylor number, which is a measure of the driving strength of the system,
$Ta$
is the Taylor number, which is a measure of the driving strength of the system,
Note that the pressure in the equations above represents the ‘reduced pressure’ that incorporates the centrifugal term;
![]() $\hat{P}=p^{\prime }-(\unicode[STIX]{x1D714}_{i}^{2}d^{2}\hat{r}^{2}/2r_{i}^{2}|\unicode[STIX]{x1D714}_{i}-\unicode[STIX]{x1D714}_{o}|^{2})\boldsymbol{e}_{r}$
with
$\hat{P}=p^{\prime }-(\unicode[STIX]{x1D714}_{i}^{2}d^{2}\hat{r}^{2}/2r_{i}^{2}|\unicode[STIX]{x1D714}_{i}-\unicode[STIX]{x1D714}_{o}|^{2})\boldsymbol{e}_{r}$
with
![]() $p=\unicode[STIX]{x1D70C}r_{i}^{2}|\unicode[STIX]{x1D714}_{i}-\unicode[STIX]{x1D714}_{o}|^{2}p^{\prime }$
and
$p=\unicode[STIX]{x1D70C}r_{i}^{2}|\unicode[STIX]{x1D714}_{i}-\unicode[STIX]{x1D714}_{o}|^{2}p^{\prime }$
and
![]() $p$
is the physical pressure. It is directly clear that the centrifugal force in TC flow is analogous to the gravitational force in RB flow (Eckhardt et al.
Reference Eckhardt, Grossmann and Lohse2007). The final term on the right-hand side of (2.1) and (2.2) gives the Coriolis force, with
$p$
is the physical pressure. It is directly clear that the centrifugal force in TC flow is analogous to the gravitational force in RB flow (Eckhardt et al.
Reference Eckhardt, Grossmann and Lohse2007). The final term on the right-hand side of (2.1) and (2.2) gives the Coriolis force, with
![]() $Ro^{-1}$
being the inverse Rossby number
$Ro^{-1}$
being the inverse Rossby number
Analogous to RB flow, the global response of TC flow can be expressed in terms of a Nusselt number. In the former, the Nusselt number expresses the dimensionless conserved heat flux, whereas in the latter the Nusselt number expresses the dimensionless conserved angular velocity flux
![]() $J^{\unicode[STIX]{x1D714}}$
, calculated by,
$J^{\unicode[STIX]{x1D714}}$
, calculated by,
with the laminar flux given by
![]() $J_{lam}^{\unicode[STIX]{x1D714}}=2\unicode[STIX]{x1D708}r_{i}^{2}r_{o}^{2}(\unicode[STIX]{x1D714}_{i}-\unicode[STIX]{x1D714}_{o})/(r_{o}^{2}-r_{i}^{2})$
where
$J_{lam}^{\unicode[STIX]{x1D714}}=2\unicode[STIX]{x1D708}r_{i}^{2}r_{o}^{2}(\unicode[STIX]{x1D714}_{i}-\unicode[STIX]{x1D714}_{o})/(r_{o}^{2}-r_{i}^{2})$
where
![]() $\unicode[STIX]{x1D708}$
is the kinematic viscosity and
$\unicode[STIX]{x1D708}$
is the kinematic viscosity and
![]() $\langle .\rangle _{\unicode[STIX]{x1D703},z,t}$
indicates averaging over the spatial directions
$\langle .\rangle _{\unicode[STIX]{x1D703},z,t}$
indicates averaging over the spatial directions
![]() $\unicode[STIX]{x1D703}$
,
$\unicode[STIX]{x1D703}$
,
![]() $z$
and time
$z$
and time
![]() $t$
. For incompressible flows, it can be derived from the NS equations that
$t$
. For incompressible flows, it can be derived from the NS equations that
![]() $J^{\unicode[STIX]{x1D714}}$
is conserved in the radial direction,
$J^{\unicode[STIX]{x1D714}}$
is conserved in the radial direction,
![]() $\unicode[STIX]{x2202}_{r}J^{\unicode[STIX]{x1D714}}=0$
(Eckhardt et al.
Reference Eckhardt, Grossmann and Lohse2007). In both cases, the values are made dimensionless by their respective laminar, conducting, values. For TC flow the Nusselt number becomes,
$\unicode[STIX]{x2202}_{r}J^{\unicode[STIX]{x1D714}}=0$
(Eckhardt et al.
Reference Eckhardt, Grossmann and Lohse2007). In both cases, the values are made dimensionless by their respective laminar, conducting, values. For TC flow the Nusselt number becomes,
The angular velocity flux
![]() $J^{\unicode[STIX]{x1D714}}$
can be written in terms of the torque
$J^{\unicode[STIX]{x1D714}}$
can be written in terms of the torque
![]() ${\mathcal{T}}$
on any of the cylinders:
${\mathcal{T}}$
on any of the cylinders:
![]() $J^{\unicode[STIX]{x1D714}}={\mathcal{T}}(2\unicode[STIX]{x03C0}L\unicode[STIX]{x1D70C})^{-1}$
with
$J^{\unicode[STIX]{x1D714}}={\mathcal{T}}(2\unicode[STIX]{x03C0}L\unicode[STIX]{x1D70C})^{-1}$
with
![]() $\unicode[STIX]{x1D70C}$
being the fluid density. Consequently, the shear stress on the inner cylinder
$\unicode[STIX]{x1D70C}$
being the fluid density. Consequently, the shear stress on the inner cylinder
![]() $\unicode[STIX]{x1D70F}_{w,i}$
is related to the angular velocity flux by
$\unicode[STIX]{x1D70F}_{w,i}$
is related to the angular velocity flux by
![]() $\unicode[STIX]{x1D70F}_{w,i}=\unicode[STIX]{x1D70C}J^{\unicode[STIX]{x1D714}}/r_{i}^{2}$
.
$\unicode[STIX]{x1D70F}_{w,i}=\unicode[STIX]{x1D70C}J^{\unicode[STIX]{x1D714}}/r_{i}^{2}$
.
Since part of our endeavour is to compare the effects of sand grain roughness on TC turbulence with the effects of sand grain roughness in other canonical systems (e.g. pipe flow), where the use of
![]() $Nu_{\unicode[STIX]{x1D714}}$
is not conventional, we choose to also present the global response in terms of the friction factor
$Nu_{\unicode[STIX]{x1D714}}$
is not conventional, we choose to also present the global response in terms of the friction factor
![]() $C_{f}$
. Here we follow Lathrop, Fineberg & Swinney (Reference Lathrop, Fineberg and Swinney1992), and define
$C_{f}$
. Here we follow Lathrop, Fineberg & Swinney (Reference Lathrop, Fineberg and Swinney1992), and define
![]() $C_{f}\equiv G/Re_{i}^{2}$
, where
$C_{f}\equiv G/Re_{i}^{2}$
, where
![]() $G$
is the dimensionless torque
$G$
is the dimensionless torque
![]() $G={\mathcal{T}}/(\unicode[STIX]{x1D70C}\unicode[STIX]{x1D708}^{2}L)$
and
$G={\mathcal{T}}/(\unicode[STIX]{x1D70C}\unicode[STIX]{x1D708}^{2}L)$
and
![]() $Re_{i}$
is the inner cylinder Reynolds number
$Re_{i}$
is the inner cylinder Reynolds number
![]() $Re_{i}=r_{i}\unicode[STIX]{x1D714}_{i}\,\text{d}/\unicode[STIX]{x1D708}$
. The translation between
$Re_{i}=r_{i}\unicode[STIX]{x1D714}_{i}\,\text{d}/\unicode[STIX]{x1D708}$
. The translation between
![]() $Nu_{\unicode[STIX]{x1D714}}$
and
$Nu_{\unicode[STIX]{x1D714}}$
and
![]() $C_{f}$
is straightforward:
$C_{f}$
is straightforward:
Note that one can also define
![]() $C_{f}\equiv 2\unicode[STIX]{x1D70F}_{w,i}/(\unicode[STIX]{x1D70C}(r_{i}\unicode[STIX]{x1D714}_{i})^{2})=(1-\unicode[STIX]{x1D702})^{2}/\unicode[STIX]{x03C0}\unicode[STIX]{x1D702}^{2}G/Re_{i}^{2}$
, which is different from (2.10) by a factor which depends on the radius ratio
$C_{f}\equiv 2\unicode[STIX]{x1D70F}_{w,i}/(\unicode[STIX]{x1D70C}(r_{i}\unicode[STIX]{x1D714}_{i})^{2})=(1-\unicode[STIX]{x1D702})^{2}/\unicode[STIX]{x03C0}\unicode[STIX]{x1D702}^{2}G/Re_{i}^{2}$
, which is different from (2.10) by a factor which depends on the radius ratio
![]() $\unicode[STIX]{x1D702}$
(Lathrop et al.
Reference Lathrop, Fineberg and Swinney1992). Here we use the definition of
$\unicode[STIX]{x1D702}$
(Lathrop et al.
Reference Lathrop, Fineberg and Swinney1992). Here we use the definition of
![]() $C_{f}$
of 2.10.
$C_{f}$
of 2.10.
3 Numerical procedure
3.1 Roughness model
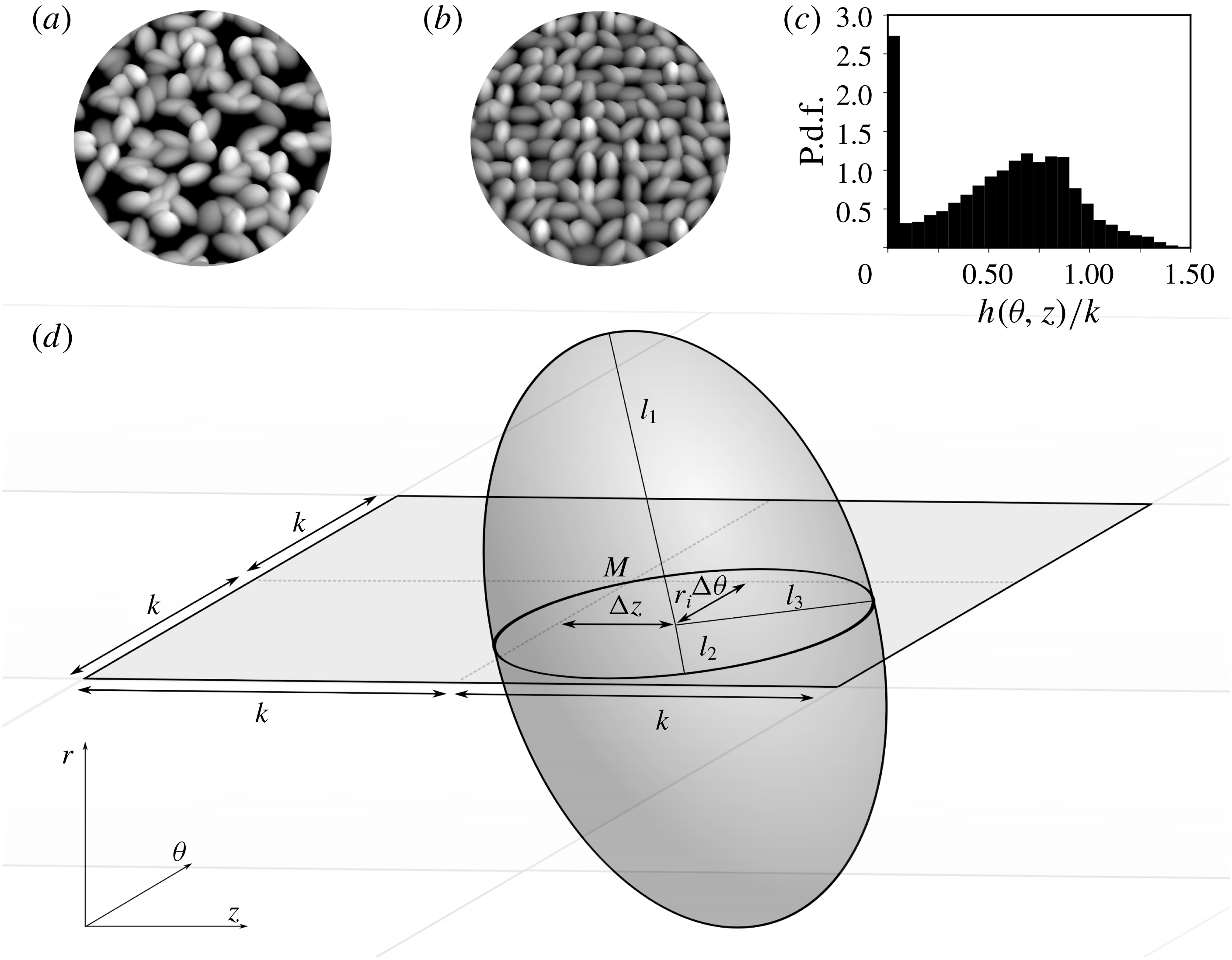
Figure 2. (a) Visual comparison between a surface with translational degrees of freedom as employed presently and (b) the original model by Scotti (Reference Scotti2006) without translational degrees of freedom. (c) Probability density function (p.d.f.) of the surface height
![]() $h(\unicode[STIX]{x1D703},z)/k$
distribution of a rough surface with 952 roughness elements (B2). For the statistics of all rough surfaces used in this study, we refer the reader to the Appendix, table 2. (d) Schematic of an ellipsoidal building block of the rough surface. Every rectangular tile of size
$h(\unicode[STIX]{x1D703},z)/k$
distribution of a rough surface with 952 roughness elements (B2). For the statistics of all rough surfaces used in this study, we refer the reader to the Appendix, table 2. (d) Schematic of an ellipsoidal building block of the rough surface. Every rectangular tile of size
![]() $2k\times 2k$
contains exactly one ellipsoid;
$2k\times 2k$
contains exactly one ellipsoid;
![]() $M$
indicates the centre of the tile. The radii
$M$
indicates the centre of the tile. The radii
![]() $l_{1}=2.0k,l_{2}=1.4k,l_{3}=1.0k$
are kept constant for each ellipsoid to maintain a monodisperse rough surface. Randomness is ensured by giving the ellipsoid five degrees of freedom; two translational shifts of the centre of the ellipsoid from the centre of the tile
$l_{1}=2.0k,l_{2}=1.4k,l_{3}=1.0k$
are kept constant for each ellipsoid to maintain a monodisperse rough surface. Randomness is ensured by giving the ellipsoid five degrees of freedom; two translational shifts of the centre of the ellipsoid from the centre of the tile
![]() $M$
, (
$M$
, (
![]() $\unicode[STIX]{x0394}z$
and
$\unicode[STIX]{x0394}z$
and
![]() $r_{i}\unicode[STIX]{x0394}\unicode[STIX]{x1D703}$
) and three rotational degrees of freedom (
$r_{i}\unicode[STIX]{x0394}\unicode[STIX]{x1D703}$
) and three rotational degrees of freedom (
![]() $\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2},\unicode[STIX]{x1D6FC}_{3}$
) from (
$\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2},\unicode[STIX]{x1D6FC}_{3}$
) from (
![]() $r,\unicode[STIX]{x1D703},z$
) to (
$r,\unicode[STIX]{x1D703},z$
) to (
![]() $l_{1},l_{2},l_{3}$
). We also employ a constant translation of the centre of the ellipsoid in the radial direction, with
$l_{1},l_{2},l_{3}$
). We also employ a constant translation of the centre of the ellipsoid in the radial direction, with
![]() $\unicode[STIX]{x0394}r=-0.5k$
from
$\unicode[STIX]{x0394}r=-0.5k$
from
![]() $r=r_{i}$
.
$r=r_{i}$
.
Figure 2 exhibits the set-up of the ‘virtual’ sand grain roughness model that is used in this research. The inner cylinder is divided up into square tiles of size
![]() $2k\times 2k$
, each tile containing exactly
$2k\times 2k$
, each tile containing exactly
![]() $1$
ellipsoid, with
$1$
ellipsoid, with
![]() $k$
the length of the minor radius of the ellipsoid. The height
$k$
the length of the minor radius of the ellipsoid. The height
![]() $L$
is slightly varied (
$L$
is slightly varied (
![]() $0.85r_{i}\pm 0.03r_{i}$
) to ensure that an integer amount of tiles fits into the domain. Unlike in the original model by Scotti (Reference Scotti2006), we also introduce a random translation of the centre of the ellipsoid by applying
$0.85r_{i}\pm 0.03r_{i}$
) to ensure that an integer amount of tiles fits into the domain. Unlike in the original model by Scotti (Reference Scotti2006), we also introduce a random translation of the centre of the ellipsoid by applying
![]() $r_{i}\unicode[STIX]{x0394}\unicode[STIX]{x1D703}$
and
$r_{i}\unicode[STIX]{x0394}\unicode[STIX]{x1D703}$
and
![]() $\unicode[STIX]{x0394}z$
, where
$\unicode[STIX]{x0394}z$
, where
![]() $r_{i}\unicode[STIX]{x0394}\unicode[STIX]{x1D703}$
, and
$r_{i}\unicode[STIX]{x0394}\unicode[STIX]{x1D703}$
, and
![]() $\unicode[STIX]{x0394}z$
are random uniform translations from the centre of the
$\unicode[STIX]{x0394}z$
are random uniform translations from the centre of the
![]() $2k\times 2k$
tile. This random translation allows for the surface to be more irregular and as such to relate more closely to a realistic sand grain surface. As also introduced by Scotti (Reference Scotti2006), we employ a constant translation of the centre of the ellipsoid in the radial direction, with
$2k\times 2k$
tile. This random translation allows for the surface to be more irregular and as such to relate more closely to a realistic sand grain surface. As also introduced by Scotti (Reference Scotti2006), we employ a constant translation of the centre of the ellipsoid in the radial direction, with
![]() $\unicode[STIX]{x0394}r=-0.5k$
from
$\unicode[STIX]{x0394}r=-0.5k$
from
![]() $r=r_{i}$
. It is shown in figure 1(a) that part of the cylinder (
$r=r_{i}$
. It is shown in figure 1(a) that part of the cylinder (
![]() ${\approx}15\,\%$
) is not covered by rough elements. The projected area of the ellipsoids equals the area of the inner cylinder that is rough. This means that the surface is not ‘overhanging’, resulting from the offset of the centre of the ellipsoid in the radial direction
${\approx}15\,\%$
) is not covered by rough elements. The projected area of the ellipsoids equals the area of the inner cylinder that is rough. This means that the surface is not ‘overhanging’, resulting from the offset of the centre of the ellipsoid in the radial direction
![]() $\unicode[STIX]{x0394}r=-0.5k$
. This makes the computations significantly less involved. By saying that part of the surface is not covered by rough elements, we mean that the neighbouring ellipsoids do not close the entire surface. This could be achieved by stacking multiple layers of ellipsoids. Statistics of the rough surfaces are found in the Appendix, table 2.
$\unicode[STIX]{x0394}r=-0.5k$
. This makes the computations significantly less involved. By saying that part of the surface is not covered by rough elements, we mean that the neighbouring ellipsoids do not close the entire surface. This could be achieved by stacking multiple layers of ellipsoids. Statistics of the rough surfaces are found in the Appendix, table 2.
3.2 Numerical method
The NS equations are spatially discretized by using a central second-order finite-difference scheme and solved in cylindrical coordinates by means of a semi-implicit procedure (Verzicco & Orlandi Reference Verzicco and Orlandi1996; van der Poel et al. Reference van der Poel, Ostilla-Mónico, Donners and Verzicco2015a ). The staggered grid is homogeneous in both the spanwise and streamwise directions (the axial and azimuthal directions respectively). We apply no-slip boundary conditions at the cylinder walls and axially periodic boundary conditions at the top and bottom.
The wall-normal grid consists of a double cosine (Chebyshev-type) grid stretching. Below the maximum roughness height, we employ a cosine stretching such that the maximum grid spacing is always smaller than 0.5 times the viscous length scale. In the bulk of the fluid, we employ a second stretching, such that the maximum grid spacing in the bulk is approximately 1.5 times the viscous length scale. The minimum grid spacing is located at the position of the maximum roughness height, where we expect the highest shear stress, see table 1 for the exact values.
Time advancement is performed by using a fractional-step third-order Runge–Kutta scheme in combination with a Crank–Nicolson scheme for the implicit terms. The Courant–Friedrichs–Lewy (CFL) (
![]() $U\unicode[STIX]{x0394}t/\unicode[STIX]{x0394}x<0.8$
, with
$U\unicode[STIX]{x0394}t/\unicode[STIX]{x0394}x<0.8$
, with
![]() $\unicode[STIX]{x0394}x$
being the grid size, and
$\unicode[STIX]{x0394}x$
being the grid size, and
![]() $U$
the velocity, both in the respective coordinate direction) condition is tested in all directions and accordingly the time-step constraint for the nonlinear terms is enforced to ensure stability.
$U$
the velocity, both in the respective coordinate direction) condition is tested in all directions and accordingly the time-step constraint for the nonlinear terms is enforced to ensure stability.
Sand grain roughness is implemented in the code by an immersed boundary method (IBM) (Fadlun et al.
Reference Fadlun, Verzicco, Orlandi and Mohd-Yusof2000). In the IBM, the boundary conditions are enforced by adding a body force
![]() $\boldsymbol{f}$
to the momentum (2.1–2.3). A regular, non-body fitting, mesh can thus be used, even though the rough boundary has a very complex geometry. We perform linear interpolation in the spatial direction for which the component of the normal surface vector is largest. The IBM has been validated previously (Fadlun et al.
Reference Fadlun, Verzicco, Orlandi and Mohd-Yusof2000; Iaccarino & Verzicco Reference Iaccarino and Verzicco2003; Stringano, Pascazio & Verzicco Reference Stringano, Pascazio and Verzicco2006; Zhu et al.
Reference Zhu, Ostilla-Mónico, Verzicco and Lohse2016, Reference Zhu, Verzicco and Lohse2017, Reference Zhu, Verschoof, Bakhuis, Huisman, Verzicco, Sun and Lohse2018b
).
$\boldsymbol{f}$
to the momentum (2.1–2.3). A regular, non-body fitting, mesh can thus be used, even though the rough boundary has a very complex geometry. We perform linear interpolation in the spatial direction for which the component of the normal surface vector is largest. The IBM has been validated previously (Fadlun et al.
Reference Fadlun, Verzicco, Orlandi and Mohd-Yusof2000; Iaccarino & Verzicco Reference Iaccarino and Verzicco2003; Stringano, Pascazio & Verzicco Reference Stringano, Pascazio and Verzicco2006; Zhu et al.
Reference Zhu, Ostilla-Mónico, Verzicco and Lohse2016, Reference Zhu, Verzicco and Lohse2017, Reference Zhu, Verschoof, Bakhuis, Huisman, Verzicco, Sun and Lohse2018b
).
Table 1. Input parameters, numerical resolution and global response of the simulations. We run four sets of simulations, which are separated by an empty horizontal line. Within every set we keep
![]() $Ta$
constant.
$Ta$
constant.
![]() $n_{\unicode[STIX]{x1D703}}\times n_{z}$
gives the number of ellipsoids in the streamwise (
$n_{\unicode[STIX]{x1D703}}\times n_{z}$
gives the number of ellipsoids in the streamwise (
![]() $\unicode[STIX]{x1D703}$
) and spanwise (
$\unicode[STIX]{x1D703}$
) and spanwise (
![]() $z$
) directions, respectively.
$z$
) directions, respectively.
![]() $N_{ell}$
expresses the resolution (
$N_{ell}$
expresses the resolution (
![]() $N_{\unicode[STIX]{x1D703}}\times N_{z}$
) per elementary building block of size
$N_{\unicode[STIX]{x1D703}}\times N_{z}$
) per elementary building block of size
![]() $2k\times 2k$
.
$2k\times 2k$
.
![]() $N_{\unicode[STIX]{x1D703}}\times N_{z}\times N_{r}$
presents the total resolution of the computational domain.
$N_{\unicode[STIX]{x1D703}}\times N_{z}\times N_{r}$
presents the total resolution of the computational domain.
![]() $C_{f}$
is the friction factor.
$C_{f}$
is the friction factor.
![]() $Nu_{\unicode[STIX]{x1D714}}$
is the dimensionless torque.
$Nu_{\unicode[STIX]{x1D714}}$
is the dimensionless torque.
![]() $k_{s}^{+}=1.33k^{+}$
is the equivalent sand grain roughness height in viscous units, where
$k_{s}^{+}=1.33k^{+}$
is the equivalent sand grain roughness height in viscous units, where
![]() $k^{+}$
is the size of the sand grains (ellipsoids with axes
$k^{+}$
is the size of the sand grains (ellipsoids with axes
![]() $2k\times 1.4k\times k$
, see figure 2), also in viscous units.
$2k\times 1.4k\times k$
, see figure 2), also in viscous units.
![]() $Re_{\unicode[STIX]{x1D70F}}$
is the friction Reynolds number,
$Re_{\unicode[STIX]{x1D70F}}$
is the friction Reynolds number,
![]() $Re_{\unicode[STIX]{x1D70F}}=(d/2)u_{\unicode[STIX]{x1D70F},i}/\unicode[STIX]{x1D708}$
.
$Re_{\unicode[STIX]{x1D70F}}=(d/2)u_{\unicode[STIX]{x1D70F},i}/\unicode[STIX]{x1D708}$
.
![]() $r_{i}^{+}\unicode[STIX]{x0394}\unicode[STIX]{x1D703}=\unicode[STIX]{x0394}z^{+}$
the grid spacing in the streamwise and spanwise directions in viscous units and
$r_{i}^{+}\unicode[STIX]{x0394}\unicode[STIX]{x1D703}=\unicode[STIX]{x0394}z^{+}$
the grid spacing in the streamwise and spanwise directions in viscous units and
![]() $\unicode[STIX]{x0394}r^{+}$
is the minimal grid spacing, at the maximum roughness height, in the wall-normal direction in viscous units. Normalization in viscous units is done with respect to the inner cylinder, i.e.
$\unicode[STIX]{x0394}r^{+}$
is the minimal grid spacing, at the maximum roughness height, in the wall-normal direction in viscous units. Normalization in viscous units is done with respect to the inner cylinder, i.e.
![]() $u_{\unicode[STIX]{x1D70F}}=u_{\unicode[STIX]{x1D70F},i}$
.
$u_{\unicode[STIX]{x1D70F}}=u_{\unicode[STIX]{x1D70F},i}$
.

Simulations run until they become statistically stationary, such that the Nusselt
![]() $Nu_{\unicode[STIX]{x1D714}}$
number remains constant to within
$Nu_{\unicode[STIX]{x1D714}}$
number remains constant to within
![]() ${\approx}1\,\%$
, which requires
${\approx}1\,\%$
, which requires
![]() $\hat{t}\approx 200$
. Thereafter, we gather statistics until the results converge, which requires
$\hat{t}\approx 200$
. Thereafter, we gather statistics until the results converge, which requires
![]() $\hat{t}\approx 50$
. The resolution constraints of the domain are typically derived from the literature and are based on the grid spacing in ‘
$\hat{t}\approx 50$
. The resolution constraints of the domain are typically derived from the literature and are based on the grid spacing in ‘
![]() $+$
’ (viscous) units. Grid independence checks of the time-averaged statistics are performed by ensuring that
$+$
’ (viscous) units. Grid independence checks of the time-averaged statistics are performed by ensuring that
![]() $Nu_{\unicode[STIX]{x1D714}}$
remains constant with increasing grid resolution in all directions and presented along with the results in table 1. Throughout the manuscript we employ superficial averaging – both over solid and fluid regions – unless stated otherwise.
$Nu_{\unicode[STIX]{x1D714}}$
remains constant with increasing grid resolution in all directions and presented along with the results in table 1. Throughout the manuscript we employ superficial averaging – both over solid and fluid regions – unless stated otherwise.
4 Results
4.1 Roughness function
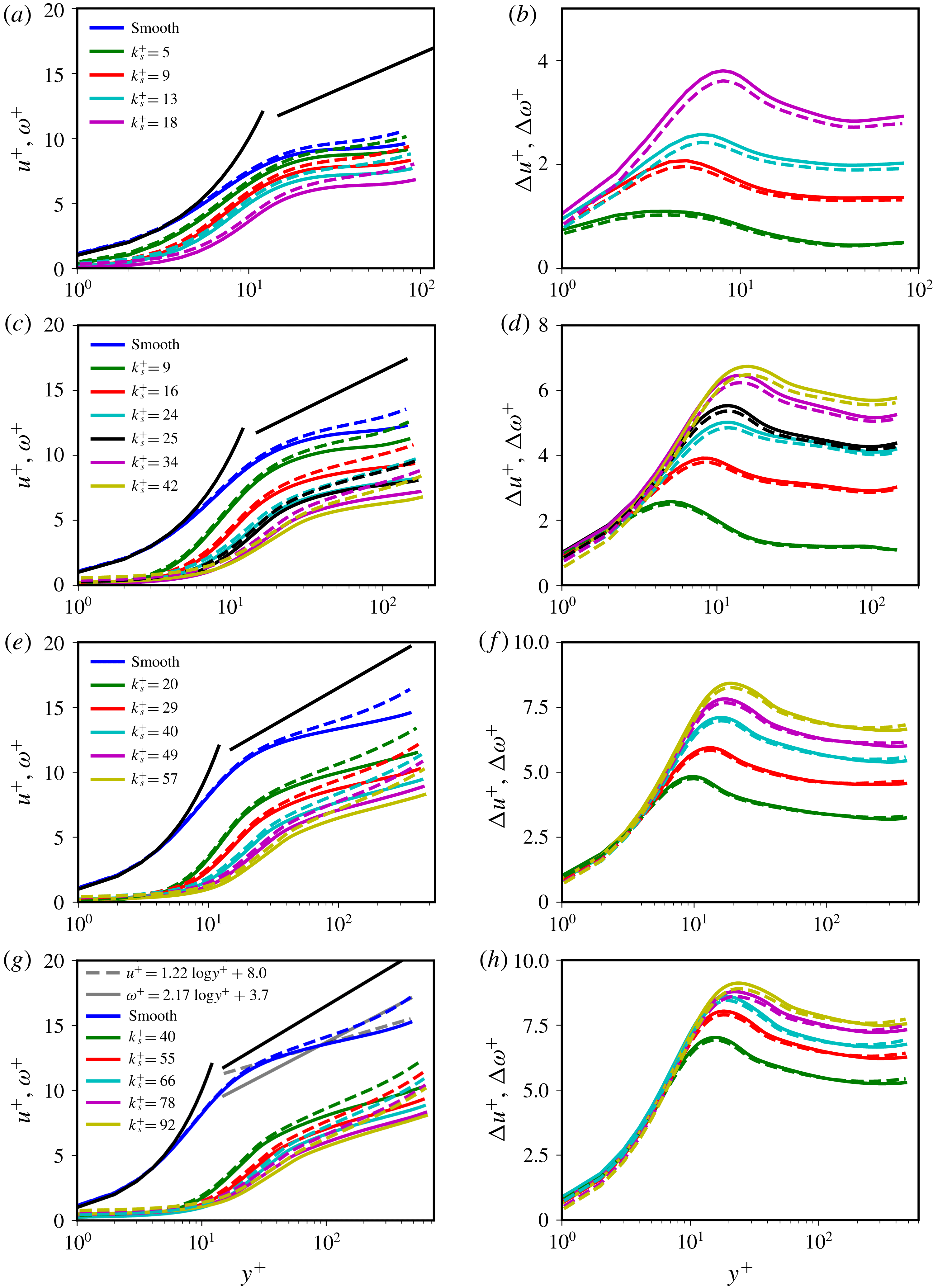
Figure 3. (a,c,e,g) Profiles of the streamwise – azimuthal – velocity
![]() $u^{+}$
(solid) and the angular velocity
$u^{+}$
(solid) and the angular velocity
![]() $\unicode[STIX]{x1D714}^{+}$
(dashed) versus the wall-normal distance
$\unicode[STIX]{x1D714}^{+}$
(dashed) versus the wall-normal distance
![]() $y^{+}$
. Black solid lines indicate the viscous sublayer profile
$y^{+}$
. Black solid lines indicate the viscous sublayer profile
![]() $u^{+}=y^{+}$
and the logarithmic law
$u^{+}=y^{+}$
and the logarithmic law
![]() $u^{+}=\unicode[STIX]{x1D705}^{-1}\log y^{+}+B$
, with
$u^{+}=\unicode[STIX]{x1D705}^{-1}\log y^{+}+B$
, with
![]() $\unicode[STIX]{x1D705}=0.4$
and
$\unicode[STIX]{x1D705}=0.4$
and
![]() $B=5.0$
. (b,d,f,h) Profiles of the streamwise velocity shift
$B=5.0$
. (b,d,f,h) Profiles of the streamwise velocity shift
![]() $\unicode[STIX]{x0394}u^{+}$
(solid) and the angular velocity shift
$\unicode[STIX]{x0394}u^{+}$
(solid) and the angular velocity shift
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D714}^{+}$
(dashed). Every row corresponds to a constant Taylor number, (a,b)
$\unicode[STIX]{x0394}\unicode[STIX]{x1D714}^{+}$
(dashed). Every row corresponds to a constant Taylor number, (a,b)
![]() $Ta=1.0\times 10^{7}$
, (c,d)
$Ta=1.0\times 10^{7}$
, (c,d)
![]() $Ta=5.0\times 10^{7}$
, (e,f)
$Ta=5.0\times 10^{7}$
, (e,f)
![]() $Ta=5.0\times 10^{8}$
and (g,h)
$Ta=5.0\times 10^{8}$
and (g,h)
![]() $Ta=1.0\times 10^{9}$
, see table 1. The grey lines in (g) are logarithmic fits to the smooth profiles for
$Ta=1.0\times 10^{9}$
, see table 1. The grey lines in (g) are logarithmic fits to the smooth profiles for
![]() $y^{+}=[150,500]$
.
$y^{+}=[150,500]$
.
Figure 3(a,c,e,g) presents the streamwise (i.e. azimuthal) velocity profiles
![]() $u^{+}=\langle u(r)-u(r_{i})\rangle _{\unicode[STIX]{x1D703},z,t}/u_{\unicode[STIX]{x1D70F}}$
(solid) and angular velocity profiles
$u^{+}=\langle u(r)-u(r_{i})\rangle _{\unicode[STIX]{x1D703},z,t}/u_{\unicode[STIX]{x1D70F}}$
(solid) and angular velocity profiles
![]() $\unicode[STIX]{x1D714}^{+}=\langle u(r_{i})-r_{i}u(r)/r\rangle _{\unicode[STIX]{x1D703},z,t}/u_{\unicode[STIX]{x1D70F}}$
(dashed) versus the wall-normal distance
$\unicode[STIX]{x1D714}^{+}=\langle u(r_{i})-r_{i}u(r)/r\rangle _{\unicode[STIX]{x1D703},z,t}/u_{\unicode[STIX]{x1D70F}}$
(dashed) versus the wall-normal distance
![]() $y^{+}=r^{+}-r_{i}^{+}-h_{m}^{+}$
, where
$y^{+}=r^{+}-r_{i}^{+}-h_{m}^{+}$
, where
![]() $\langle .\rangle _{\unicode[STIX]{x1D703},z,t}$
indicates averaging over the streamwise and spanwise directions and in time, and
$\langle .\rangle _{\unicode[STIX]{x1D703},z,t}$
indicates averaging over the streamwise and spanwise directions and in time, and
![]() $h_{m}^{+}$
is the mean roughness height. Every row corresponds to simulations at constant rotation rate of the inner cylinder (Taylor number), and increasing roughness height.
$h_{m}^{+}$
is the mean roughness height. Every row corresponds to simulations at constant rotation rate of the inner cylinder (Taylor number), and increasing roughness height.
In line with the previous observations of Huisman et al. (Reference Huisman, Scharnowski, Cierpka, Kähler, Lohse and Sun2013) and Ostilla-Mónico et al. (Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014), we also find that the logarithmic profiles of the streamwise velocity
![]() $u^{+}$
in smooth-wall TC do not fit the
$u^{+}$
in smooth-wall TC do not fit the
![]() $\unicode[STIX]{x1D705}=0.4$
slope, as found in other wall-bounded flows (e.g. pipe, boundary layer, channel) – for similar values of the friction Reynolds number
$\unicode[STIX]{x1D705}=0.4$
slope, as found in other wall-bounded flows (e.g. pipe, boundary layer, channel) – for similar values of the friction Reynolds number
![]() $Re_{\unicode[STIX]{x1D70F}}$
. However, this asymptotic value is experimentally observed at very high shear rates of
$Re_{\unicode[STIX]{x1D70F}}$
. However, this asymptotic value is experimentally observed at very high shear rates of
![]() $Ta=O(10^{12})$
and
$Ta=O(10^{12})$
and
![]() $Re_{\unicode[STIX]{x1D70F}}=O(10^{4})$
(Huisman et al.
Reference Huisman, Scharnowski, Cierpka, Kähler, Lohse and Sun2013), much higher than can be obtained by the present DNS. The logarithmic profiles of angular velocity
$Re_{\unicode[STIX]{x1D70F}}=O(10^{4})$
(Huisman et al.
Reference Huisman, Scharnowski, Cierpka, Kähler, Lohse and Sun2013), much higher than can be obtained by the present DNS. The logarithmic profiles of angular velocity
![]() $\unicode[STIX]{x1D714}^{+}$
have a slope that is closer to the
$\unicode[STIX]{x1D714}^{+}$
have a slope that is closer to the
![]() $\unicode[STIX]{x1D705}=0.4$
asymptote (Ostilla-Mónico et al.
Reference Ostilla-Mónico, Verzicco and Lohse2015), especially for the higher
$\unicode[STIX]{x1D705}=0.4$
asymptote (Ostilla-Mónico et al.
Reference Ostilla-Mónico, Verzicco and Lohse2015), especially for the higher
![]() $Ta$
figure 3(
$Ta$
figure 3(
![]() $g,h$
). Here we investigate the effects of roughness on both
$g,h$
). Here we investigate the effects of roughness on both
![]() $u^{+}$
and
$u^{+}$
and
![]() $\unicode[STIX]{x1D714}^{+}$
.
$\unicode[STIX]{x1D714}^{+}$
.
For rough-wall simulations, the logarithmic region shifts downwards – a hallmark effect of a drag increasing surface. Figure 3(b,d,f,h) presents the shifts, where
![]() $\unicode[STIX]{x0394}u^{+}=u_{s}^{+}-u_{r}^{+}$
and
$\unicode[STIX]{x0394}u^{+}=u_{s}^{+}-u_{r}^{+}$
and
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D714}^{+}=\unicode[STIX]{x1D714}_{s}^{+}-\unicode[STIX]{x1D714}_{r}^{+}$
. All shifts of the angular and azimuthal profiles are calculated at the centre of the gap, that is at
$\unicode[STIX]{x0394}\unicode[STIX]{x1D714}^{+}=\unicode[STIX]{x1D714}_{s}^{+}-\unicode[STIX]{x1D714}_{r}^{+}$
. All shifts of the angular and azimuthal profiles are calculated at the centre of the gap, that is at
![]() $y^{+}+h_{m}^{+}=Re_{\unicode[STIX]{x1D70F}}$
. As one can see in figure 3(b,d,f,h) of the manuscript, the values of
$y^{+}+h_{m}^{+}=Re_{\unicode[STIX]{x1D70F}}$
. As one can see in figure 3(b,d,f,h) of the manuscript, the values of
![]() $\unicode[STIX]{x0394}u^{+}$
and
$\unicode[STIX]{x0394}u^{+}$
and
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D714}^{+}$
do not depend on
$\unicode[STIX]{x0394}\unicode[STIX]{x1D714}^{+}$
do not depend on
![]() $y^{+}$
if one is sufficiently far away from the wall. For lower
$y^{+}$
if one is sufficiently far away from the wall. For lower
![]() $Ta$
, there is a small but observable difference between
$Ta$
, there is a small but observable difference between
![]() $\unicode[STIX]{x0394}u^{+}$
and
$\unicode[STIX]{x0394}u^{+}$
and
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D714}^{+}$
, see figure 3(b), whereas for the higher
$\unicode[STIX]{x0394}\unicode[STIX]{x1D714}^{+}$
, see figure 3(b), whereas for the higher
![]() $Ta$
, this difference diminishes, see figure 3(f,h).
$Ta$
, this difference diminishes, see figure 3(f,h).
Figure 4. (a) Azimuthal velocity shift (Hama roughness function)
![]() $\unicode[STIX]{x0394}u^{+}$
versus the equivalent sand grain roughness height
$\unicode[STIX]{x0394}u^{+}$
versus the equivalent sand grain roughness height
![]() $k_{s}^{+}$
, where
$k_{s}^{+}$
, where
![]() $k_{s}^{+}=1.33k^{+}$
. (b) Angular velocity shift
$k_{s}^{+}=1.33k^{+}$
. (b) Angular velocity shift
![]() $\unicode[STIX]{x1D714}^{+}$
versus
$\unicode[STIX]{x1D714}^{+}$
versus
![]() $k_{s}^{+}$
. Close overlap with the Nikuradse curve is observed in the transitionally rough regime. The overlap is slightly better for the angular velocity shift, for which we also obtain
$k_{s}^{+}$
. Close overlap with the Nikuradse curve is observed in the transitionally rough regime. The overlap is slightly better for the angular velocity shift, for which we also obtain
![]() $k_{s}^{+}=1.33k^{+}$
. The solid blue line represents the fully rough asymptote;
$k_{s}^{+}=1.33k^{+}$
. The solid blue line represents the fully rough asymptote;
![]() $\unicode[STIX]{x0394}u^{+}=2.44\log (k_{s}^{+})+5.2-8.5$
. The green lines represent the fully rough asymptotes obtained from the simulations, with
$\unicode[STIX]{x0394}u^{+}=2.44\log (k_{s}^{+})+5.2-8.5$
. The green lines represent the fully rough asymptotes obtained from the simulations, with
![]() $\unicode[STIX]{x1D705}_{u},\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D714}},A_{u}$
and
$\unicode[STIX]{x1D705}_{u},\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D714}},A_{u}$
and
![]() $A_{\unicode[STIX]{x1D714}}$
extracted from figure 3(g). The spread between statistically similar surfaces, with similar mean and maximum heights, is indicated by the vertical bar.
$A_{\unicode[STIX]{x1D714}}$
extracted from figure 3(g). The spread between statistically similar surfaces, with similar mean and maximum heights, is indicated by the vertical bar.
![]() $k_{s}$
is determinded by a best fit between the two data points in the fully rough regime (i.e. cases D4 and D5, see table 1) and the Nikuradse fully rough asymptote.
$k_{s}$
is determinded by a best fit between the two data points in the fully rough regime (i.e. cases D4 and D5, see table 1) and the Nikuradse fully rough asymptote.
Figure 5. (a) Azimuthal velocity
![]() $u^{+}$
(solid) and the angular velocity
$u^{+}$
(solid) and the angular velocity
![]() $\unicode[STIX]{x1D714}^{+}$
(dashed) versus the wall-normal distance
$\unicode[STIX]{x1D714}^{+}$
(dashed) versus the wall-normal distance
![]() $y/k_{s}$
, where
$y/k_{s}$
, where
![]() $y=(r-h_{m})$
and
$y=(r-h_{m})$
and
![]() $h_{m}$
is the mean roughness height. The three simulations with the highest roughness are plotted (D3, D4 and D5 respectively, see table 1) to convey collapse of the profiles for the fully rough cases. (b) The Nikuradse constant
$h_{m}$
is the mean roughness height. The three simulations with the highest roughness are plotted (D3, D4 and D5 respectively, see table 1) to convey collapse of the profiles for the fully rough cases. (b) The Nikuradse constant
![]() $\tilde{B}$
versus the equivalent sand grain roughness height
$\tilde{B}$
versus the equivalent sand grain roughness height
![]() $k_{s}^{+}$
for both the azimuthal velocity (squares) and the angular velocity (diamonds). Horizontal black line at
$k_{s}^{+}$
for both the azimuthal velocity (squares) and the angular velocity (diamonds). Horizontal black line at
![]() $\tilde{B}=6.0$
gives the asymptotic value that is observed for fully rough behaviour.
$\tilde{B}=6.0$
gives the asymptotic value that is observed for fully rough behaviour.
Figure 4(a,b) presents the shift of the streamwise and angular velocity profiles, respectively, versus the equivalent roughness height
![]() $k_{s}^{+}$
, for all
$k_{s}^{+}$
, for all
![]() $Ta$
. Care is taken to ensure overlap for varying
$Ta$
. Care is taken to ensure overlap for varying
![]() $Ta$
and similar
$Ta$
and similar
![]() $k^{+}$
, to study the
$k^{+}$
, to study the
![]() $Ta$
dependence of
$Ta$
dependence of
![]() $\unicode[STIX]{x0394}u^{+}$
and
$\unicode[STIX]{x0394}u^{+}$
and
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D714}^{+}$
. However, despite the varying
$\unicode[STIX]{x0394}\unicode[STIX]{x1D714}^{+}$
. However, despite the varying
![]() $Ta$
numbers, all data collapse onto a single curve, with some scatter. Note that scatter is expected due to the randomness of the surfaces, which are reproduced for every simulation. To obtain an estimate of the expected scatter, we run two simulations with statistically similar surfaces. These are indicated by B3 and BY in table 1 and the velocity profiles are found in figure 3(c,d). We find a difference between the two cases of
$Ta$
numbers, all data collapse onto a single curve, with some scatter. Note that scatter is expected due to the randomness of the surfaces, which are reproduced for every simulation. To obtain an estimate of the expected scatter, we run two simulations with statistically similar surfaces. These are indicated by B3 and BY in table 1 and the velocity profiles are found in figure 3(c,d). We find a difference between the two cases of
![]() ${\lesssim}0.2\unicode[STIX]{x0394}u^{+},0.2\unicode[STIX]{x0394}\unicode[STIX]{x1D714}^{+}$
. The measure of this scatter is indicated in figure 4 as a vertical bar (
${\lesssim}0.2\unicode[STIX]{x0394}u^{+},0.2\unicode[STIX]{x0394}\unicode[STIX]{x1D714}^{+}$
. The measure of this scatter is indicated in figure 4 as a vertical bar (
![]() $=$
spread). We figure 4 as a vertical bar (
$=$
spread). We figure 4 as a vertical bar (
![]() $=$
spread). We conclude that the variability in
$=$
spread). We conclude that the variability in
![]() $\unicode[STIX]{x0394}u^{+}$
and
$\unicode[STIX]{x0394}u^{+}$
and
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D714}^{+}$
at constant
$\unicode[STIX]{x0394}\unicode[STIX]{x1D714}^{+}$
at constant
![]() $k^{+}$
and varying
$k^{+}$
and varying
![]() $Ta$
falls within the size of that vertical bar, and such conclude that
$Ta$
falls within the size of that vertical bar, and such conclude that
![]() $\unicode[STIX]{x0394}u^{+}$
and
$\unicode[STIX]{x0394}u^{+}$
and
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D714}^{+}$
and thus the equivalent roughness height
$\unicode[STIX]{x0394}\unicode[STIX]{x1D714}^{+}$
and thus the equivalent roughness height
![]() $k_{s}^{+}$
shows little dependence on
$k_{s}^{+}$
shows little dependence on
![]() $Ta$
.
$Ta$
.
A comparison with the findings of Nikuradse (Reference Nikuradse1933) can be carried out by scaling the fully rough regime to obtain
![]() $k_{s}^{+}=Ck^{+}$
, where
$k_{s}^{+}=Ck^{+}$
, where
![]() $C$
is a constant that depends on the surface topology. In figure 5(a) we plot the velocity profiles versus
$C$
is a constant that depends on the surface topology. In figure 5(a) we plot the velocity profiles versus
![]() $(r-h_{m})/k_{s}$
for the highest roughness (D3, D4 and D5 respectively, see table 1). Excellent collapse of the D4 and D5 profiles indicates that those simulations are indeed fully rough. In this fully rough regime viscosity can be neglected (
$(r-h_{m})/k_{s}$
for the highest roughness (D3, D4 and D5 respectively, see table 1). Excellent collapse of the D4 and D5 profiles indicates that those simulations are indeed fully rough. In this fully rough regime viscosity can be neglected (
![]() $y\gg k\gg \unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D708}}$
), whereas the velocity profile is also independent of the system outer length scales (
$y\gg k\gg \unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D708}}$
), whereas the velocity profile is also independent of the system outer length scales (
![]() $y\ll d$
) i.e. the overlap argument (Pope Reference Pope2000). The gradient of the velocity profile becomes
$y\ll d$
) i.e. the overlap argument (Pope Reference Pope2000). The gradient of the velocity profile becomes
![]() $\text{d}\langle U\rangle /\text{d}y=(u_{\unicode[STIX]{x1D70F}}/y)\unicode[STIX]{x1D6F7}(y/k)$
, where
$\text{d}\langle U\rangle /\text{d}y=(u_{\unicode[STIX]{x1D70F}}/y)\unicode[STIX]{x1D6F7}(y/k)$
, where
![]() $\unicode[STIX]{x1D6F7}(y/k)$
is a universal function that will go to
$\unicode[STIX]{x1D6F7}(y/k)$
is a universal function that will go to
![]() $1/\unicode[STIX]{x1D705}$
. Integration then gives
$1/\unicode[STIX]{x1D705}$
. Integration then gives
where
![]() $B$
is a constant and
$B$
is a constant and
![]() $y=r-h_{m}$
;
$y=r-h_{m}$
;
![]() $\tilde{B}$
is the Nikuradse constant. The roughness function in the fully rough regime, (i.e. the fully rough asymptote), is obtained by subtracting (4.1) from the smooth-wall profile
$\tilde{B}$
is the Nikuradse constant. The roughness function in the fully rough regime, (i.e. the fully rough asymptote), is obtained by subtracting (4.1) from the smooth-wall profile
![]() $u_{s}^{+}=(1/\unicode[STIX]{x1D705})\log (y^{+})+A$
and rescaling it to overlap with the Nikuradse data,
$u_{s}^{+}=(1/\unicode[STIX]{x1D705})\log (y^{+})+A$
and rescaling it to overlap with the Nikuradse data,
In figure 4(a), the blue solid line is the fully rough asymptote, with
![]() $\unicode[STIX]{x1D705},A,\tilde{B}$
as found in pipe flow (Pope Reference Pope2000). The green solid line is the fully rough asymptote as obtained from our simulations;
$\unicode[STIX]{x1D705},A,\tilde{B}$
as found in pipe flow (Pope Reference Pope2000). The green solid line is the fully rough asymptote as obtained from our simulations;
![]() $\unicode[STIX]{x1D705}_{u}^{-1}=1.22$
and
$\unicode[STIX]{x1D705}_{u}^{-1}=1.22$
and
![]() $A_{u}=8.0$
are taken from the fit of the smooth-wall simulation at identical
$A_{u}=8.0$
are taken from the fit of the smooth-wall simulation at identical
![]() $Ta$
as the fully rough cases (figure 3
g). The fits are in the domain
$Ta$
as the fully rough cases (figure 3
g). The fits are in the domain
![]() $y^{+}=[150,500]$
, as there the slope becomes approximately constant (figure 3
h). The value of
$y^{+}=[150,500]$
, as there the slope becomes approximately constant (figure 3
h). The value of
![]() $\tilde{B}$
is plotted in figure 5(b), where we find that
$\tilde{B}$
is plotted in figure 5(b), where we find that
![]() $\tilde{B}\approx 6.0$
for the fully rough cases. The mismatch of the slopes in the fully rough regime makes a rescaling to find
$\tilde{B}\approx 6.0$
for the fully rough cases. The mismatch of the slopes in the fully rough regime makes a rescaling to find
![]() $k_{s}^{+}$
a priori impossible – a statement that we wish to emphasize. However, to proceed with the comparison of the transitionally rough cases in TC and pipe flow, we choose to rescale the fully rough cases (D4 and D5) with the Nikuradse fully rough asymptote in figure 4. We find that
$k_{s}^{+}$
a priori impossible – a statement that we wish to emphasize. However, to proceed with the comparison of the transitionally rough cases in TC and pipe flow, we choose to rescale the fully rough cases (D4 and D5) with the Nikuradse fully rough asymptote in figure 4. We find that
![]() $k_{s}^{+}=1.33k^{+}$
and very close collapse of our data with the Nikuradse data.
$k_{s}^{+}=1.33k^{+}$
and very close collapse of our data with the Nikuradse data.
In parallel, we analyse the behaviour of
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D714}^{+}$
versus
$\unicode[STIX]{x0394}\unicode[STIX]{x1D714}^{+}$
versus
![]() $k_{s}^{+}$
, shown in figure 4(b). Again, the blue solid line represents the fully rough asymptote of Nikuradse. The green solid line is the fully rough asymptote obtained from fits (
$k_{s}^{+}$
, shown in figure 4(b). Again, the blue solid line represents the fully rough asymptote of Nikuradse. The green solid line is the fully rough asymptote obtained from fits (
![]() $y^{+}=[150,500]$
) of the smooth-wall angular velocity profile at identical
$y^{+}=[150,500]$
) of the smooth-wall angular velocity profile at identical
![]() $Ta$
as the fully rough cases, see figure 3(g). We find
$Ta$
as the fully rough cases, see figure 3(g). We find
![]() $\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D714}}^{-1}=2.17$
(
$\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D714}}^{-1}=2.17$
(
![]() $A_{\unicode[STIX]{x1D714}}=3.7$
), close to the asymptotic value
$A_{\unicode[STIX]{x1D714}}=3.7$
), close to the asymptotic value
![]() $\unicode[STIX]{x1D705}^{-1}=2.44$
. Although the differences are marginal,
$\unicode[STIX]{x1D705}^{-1}=2.44$
. Although the differences are marginal,
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D714}^{+}$
fits to the Nikuradse data slightly better than
$\unicode[STIX]{x0394}\unicode[STIX]{x1D714}^{+}$
fits to the Nikuradse data slightly better than
![]() $\unicode[STIX]{x0394}u^{+}$
(note that also here the rescaling is,
$\unicode[STIX]{x0394}u^{+}$
(note that also here the rescaling is,
![]() $k_{s}=1.33k$
). However, the major difference is the closeness of the fully rough asymptotes.
$k_{s}=1.33k$
). However, the major difference is the closeness of the fully rough asymptotes.
These results suggest that the near-wall effects of transitionally rough sand grains (and other rough surfaces) in TC flow are similar to the effects of transitionally rough sand grains (and other rough surfaces) in pipe flow (and other canonical systems). Further, we find that these transitionally rough effects are independent of slope of the velocity profile in the logarithmic region, whereas in the fully rough regime, they, a priori, depend on this slope. This is confirmed with similar values of
![]() $\unicode[STIX]{x0394}u^{+}$
at similar
$\unicode[STIX]{x0394}u^{+}$
at similar
![]() $k_{s}^{+}$
, for varying
$k_{s}^{+}$
, for varying
![]() $Ta$
, see figure 4. Also the similarity between
$Ta$
, see figure 4. Also the similarity between
![]() $\unicode[STIX]{x0394}u^{+}$
and
$\unicode[STIX]{x0394}u^{+}$
and
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D714}^{+}$
in the transitionally rough regime confirms this, whereas the fully rough asymptotes are very dissimilar. We like to point out that simulations (or experiments) at high enough
$\unicode[STIX]{x0394}\unicode[STIX]{x1D714}^{+}$
in the transitionally rough regime confirms this, whereas the fully rough asymptotes are very dissimilar. We like to point out that simulations (or experiments) at high enough
![]() $Ta$
(
$Ta$
(
![]() $=10^{12}$
(Huisman et al.
Reference Huisman, Scharnowski, Cierpka, Kähler, Lohse and Sun2013)), where
$=10^{12}$
(Huisman et al.
Reference Huisman, Scharnowski, Cierpka, Kähler, Lohse and Sun2013)), where
![]() $\unicode[STIX]{x1D705}=0.4$
, then are expected to also give a collapse to the Nikuradse data in the fully rough regime.
$\unicode[STIX]{x1D705}=0.4$
, then are expected to also give a collapse to the Nikuradse data in the fully rough regime.
4.2 Global response

Figure 6. Profiles of (a) the friction factor
![]() $C_{f}$
, and (b) the Nusselt number
$C_{f}$
, and (b) the Nusselt number
![]() $Nu_{\unicode[STIX]{x1D714}}$
versus the roughness height.
$Nu_{\unicode[STIX]{x1D714}}$
versus the roughness height.
![]() $k/d$
is the roughness height
$k/d$
is the roughness height
![]() $k$
relative to the gap width
$k$
relative to the gap width
![]() $d$
. (c) Normalized friction coefficient
$d$
. (c) Normalized friction coefficient
![]() $C_{f}(k_{s}^{+})/C_{f}(k_{s}^{+}=0)$
versus the equivalent sand grain roughness height
$C_{f}(k_{s}^{+})/C_{f}(k_{s}^{+}=0)$
versus the equivalent sand grain roughness height
![]() $k_{s}^{+}$
. (d) Normalized Nusselt number
$k_{s}^{+}$
. (d) Normalized Nusselt number
![]() $Nu_{\unicode[STIX]{x1D714}}(k_{s}^{+})/Nu_{\unicode[STIX]{x1D714}}(k_{s}^{+}=0)$
versus the equivalent sand grain roughness height
$Nu_{\unicode[STIX]{x1D714}}(k_{s}^{+})/Nu_{\unicode[STIX]{x1D714}}(k_{s}^{+}=0)$
versus the equivalent sand grain roughness height
![]() $k_{s}^{+}$
.
$k_{s}^{+}$
.
Figure 6(a) presents the friction factor
![]() $C_{f}$
versus the dimensionless roughness height
$C_{f}$
versus the dimensionless roughness height
![]() $k/d$
for varying
$k/d$
for varying
![]() $Re_{i}$
. For lower
$Re_{i}$
. For lower
![]() $Ta$
numbers, the friction factor
$Ta$
numbers, the friction factor
![]() $C_{f}$
decreases with increasing
$C_{f}$
decreases with increasing
![]() $Ta$
, indicating the relevance of viscous drag. For the two highest
$Ta$
, indicating the relevance of viscous drag. For the two highest
![]() $Ta$
numbers, representing the higher
$Ta$
numbers, representing the higher
![]() $k_{s}^{+}$
cases, the friction factor almost collapses onto one line. This tells that
$k_{s}^{+}$
cases, the friction factor almost collapses onto one line. This tells that
![]() $\unicode[STIX]{x1D70F}_{w}\propto u^{2}$
, and thus that pressure drag is dominant over viscous drag, in accordance with the overlap argument presented above. For constant
$\unicode[STIX]{x1D70F}_{w}\propto u^{2}$
, and thus that pressure drag is dominant over viscous drag, in accordance with the overlap argument presented above. For constant
![]() $Ta$
, as expected, the friction factor increases for increasing roughness height. Figure 6(b) presents the global response in terms of
$Ta$
, as expected, the friction factor increases for increasing roughness height. Figure 6(b) presents the global response in terms of
![]() $Nu_{\unicode[STIX]{x1D714}}$
. We observe an increase in
$Nu_{\unicode[STIX]{x1D714}}$
. We observe an increase in
![]() $Nu_{\unicode[STIX]{x1D714}}$
for increasing
$Nu_{\unicode[STIX]{x1D714}}$
for increasing
![]() $Ta$
, corresponding to the increased transport of the angular velocity that is due to the increased turbulent mixing. Higher roughness leads to increased
$Ta$
, corresponding to the increased transport of the angular velocity that is due to the increased turbulent mixing. Higher roughness leads to increased
![]() $J^{\unicode[STIX]{x1D714}}$
as compared to the smooth wall at the same
$J^{\unicode[STIX]{x1D714}}$
as compared to the smooth wall at the same
![]() $Ta$
, which also relates to a higher intensity of the turbulent mixing (the
$Ta$
, which also relates to a higher intensity of the turbulent mixing (the
![]() $r^{3}(\langle w\unicode[STIX]{x1D714}\rangle _{\unicode[STIX]{x1D703},z,t})$
term of (2.8)) and more plumes ejecting from the boundary layer radially outwards (Zhu et al.
Reference Zhu, Verzicco and Lohse2017), on which we will elaborate in § 4.3.
$r^{3}(\langle w\unicode[STIX]{x1D714}\rangle _{\unicode[STIX]{x1D703},z,t})$
term of (2.8)) and more plumes ejecting from the boundary layer radially outwards (Zhu et al.
Reference Zhu, Verzicco and Lohse2017), on which we will elaborate in § 4.3.
By assuming a logarithmic profile, and integrating this profile over the entire gap (thereby neglecting the contributions of the viscous sublayer), we arrive at an implicit equation for the friction factor
![]() $C_{f}$
, namely the celebrated Prandtl’s friction law,
$C_{f}$
, namely the celebrated Prandtl’s friction law,
where
![]() $C_{1}(Re_{i})$
and
$C_{1}(Re_{i})$
and
![]() $C_{2}(Re_{i})$
for TC at these
$C_{2}(Re_{i})$
for TC at these
![]() $Re_{i}$
. Figure 7 shows the friction factor
$Re_{i}$
. Figure 7 shows the friction factor
![]() $C_{f}$
versus the inner cylinder Reynolds number
$C_{f}$
versus the inner cylinder Reynolds number
![]() $Re_{i}$
, for both smooth-wall (solid) as the rough-wall (symbols) simulations. An upward shift of the friction factor for increasing roughness height is consistent with what is observed for sand grains in pipe flow (Nikuradse Reference Nikuradse1933) and recently also for transverse ribs in Taylor–Couette flow (Zhu et al.
Reference Zhu, Verschoof, Bakhuis, Huisman, Verzicco, Sun and Lohse2018b
). Note that this upward shift is directly related to the downward shift of the mean streamwise velocity profile (the roughness function). Since the friction factor and the Nusselt number are related, as expressed in (2.10), we expect the Nusselt number to increase, for increasing roughness height. This is confirmed in figure 7(b), where we plot the Nu number versus the Ta number. The number of simulations with constant
$Re_{i}$
, for both smooth-wall (solid) as the rough-wall (symbols) simulations. An upward shift of the friction factor for increasing roughness height is consistent with what is observed for sand grains in pipe flow (Nikuradse Reference Nikuradse1933) and recently also for transverse ribs in Taylor–Couette flow (Zhu et al.
Reference Zhu, Verschoof, Bakhuis, Huisman, Verzicco, Sun and Lohse2018b
). Note that this upward shift is directly related to the downward shift of the mean streamwise velocity profile (the roughness function). Since the friction factor and the Nusselt number are related, as expressed in (2.10), we expect the Nusselt number to increase, for increasing roughness height. This is confirmed in figure 7(b), where we plot the Nu number versus the Ta number. The number of simulations with constant
![]() $k/d$
is limited, and we vary the Ta number over 2 decades only. However, we observe that the asymptotic, ultimate scaling of
$k/d$
is limited, and we vary the Ta number over 2 decades only. However, we observe that the asymptotic, ultimate scaling of
![]() $Nu_{\unicode[STIX]{x1D714}}\propto Ta^{0.5}$
, as found for fully rough transverse ribs in (Zhu et al.
Reference Zhu, Verschoof, Bakhuis, Huisman, Verzicco, Sun and Lohse2018b
), is not reached. This is expected, as only the inner cylinder is covered with roughness.
$Nu_{\unicode[STIX]{x1D714}}\propto Ta^{0.5}$
, as found for fully rough transverse ribs in (Zhu et al.
Reference Zhu, Verschoof, Bakhuis, Huisman, Verzicco, Sun and Lohse2018b
), is not reached. This is expected, as only the inner cylinder is covered with roughness.
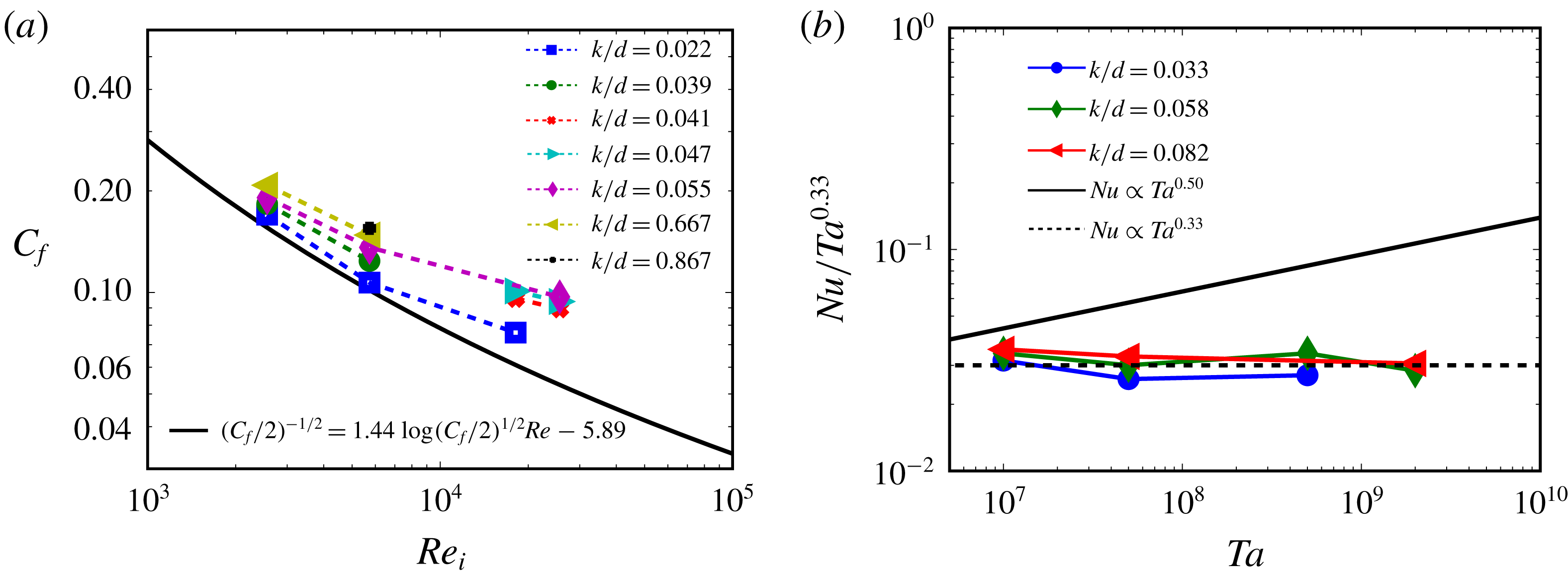
Figure 7. (a) Moody representation, showing the friction factor
![]() $C_{f}$
as a function of the inner cylinder Reynolds number
$C_{f}$
as a function of the inner cylinder Reynolds number
![]() $Re_{i}$
for varying roughness height
$Re_{i}$
for varying roughness height
![]() $k/d$
. The solid line is the fit of the Prandtl friction law to the smooth-wall simulation data. (b) Compensated plot of the Nusselt number versus the Taylor number for constant
$k/d$
. The solid line is the fit of the Prandtl friction law to the smooth-wall simulation data. (b) Compensated plot of the Nusselt number versus the Taylor number for constant
![]() $k/d$
. In this regime,
$k/d$
. In this regime,
![]() $Nu\propto Ta^{0.33}$
. The solid black line indicates the asymptotic scaling of
$Nu\propto Ta^{0.33}$
. The solid black line indicates the asymptotic scaling of
![]() $Nu\propto Ta^{0.50}$
.
$Nu\propto Ta^{0.50}$
.
4.3 Flow structures
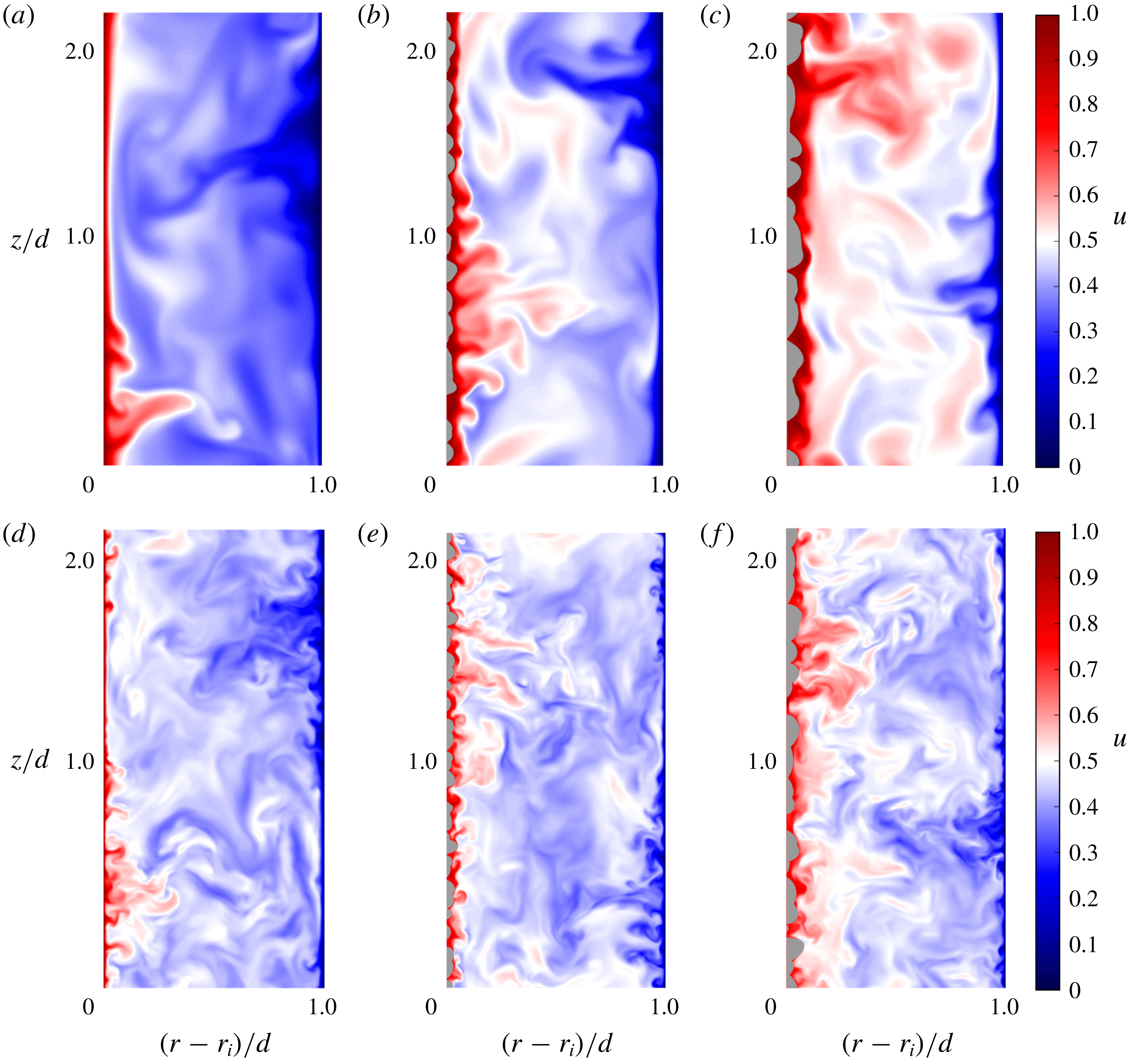
Figure 8. (a–c) Classical turbulent state: contour fields of the instantaneous azimuthal velocity
![]() $u(r,\unicode[STIX]{x1D703},z,t)$
for
$u(r,\unicode[STIX]{x1D703},z,t)$
for
![]() $Ta=5.0\times 10^{7}$
in the meridional plane. (a) Smooth-wall simulation (BS) in which we observe one ejecting plume and one impacting plume. (b) Rough inner cylinder
$Ta=5.0\times 10^{7}$
in the meridional plane. (a) Smooth-wall simulation (BS) in which we observe one ejecting plume and one impacting plume. (b) Rough inner cylinder
![]() $k/d=0.039$
(B2), with the roughness indicated in grey, exhibiting more plumes ejecting from the inner cylinder radially outwards. (c) Rough inner cylinder
$k/d=0.039$
(B2), with the roughness indicated in grey, exhibiting more plumes ejecting from the inner cylinder radially outwards. (c) Rough inner cylinder
![]() $k/d=0.073$
, with the roughness indicated in grey, (B4) leading to a more chaotic flow field, with enhanced mixing and enhanced radial transport of the conserved angular velocity flux. (d–f) Ultimate turbulent state: contour fields of the instantaneous azimuthal velocity
$k/d=0.073$
, with the roughness indicated in grey, (B4) leading to a more chaotic flow field, with enhanced mixing and enhanced radial transport of the conserved angular velocity flux. (d–f) Ultimate turbulent state: contour fields of the instantaneous azimuthal velocity
![]() $u(r,\unicode[STIX]{x1D703},z,t)$
for
$u(r,\unicode[STIX]{x1D703},z,t)$
for
![]() $Ta=1.0\times 10^{9}$
in the meridional plane. (d) Smooth inner cylinder (DS) with many plumes ejecting, considerably more chaotic than in (a). (e) Inner cylinder wall roughness (indicated in grey)
$Ta=1.0\times 10^{9}$
in the meridional plane. (d) Smooth inner cylinder (DS) with many plumes ejecting, considerably more chaotic than in (a). (e) Inner cylinder wall roughness (indicated in grey)
![]() $k/d=0.035$
(D2) and (f) inner wall roughness
$k/d=0.035$
(D2) and (f) inner wall roughness
![]() $k/d=0.055$
(D5). For the rough cases, we observe more plumes ejecting and more mixing in the bulk, leading to enhanced radial transport of the angular velocity
$k/d=0.055$
(D5). For the rough cases, we observe more plumes ejecting and more mixing in the bulk, leading to enhanced radial transport of the angular velocity
![]() $J^{\unicode[STIX]{x1D714}}$
, expressed in a higher
$J^{\unicode[STIX]{x1D714}}$
, expressed in a higher
![]() $Nu_{\unicode[STIX]{x1D714}}$
.
$Nu_{\unicode[STIX]{x1D714}}$
.
To obtain a qualitative understanding of the effect of inner cylinder roughness on the turbulent flow in the gap, we present two series of snapshots of the streamwise azimuthal velocity
![]() $u(r,\unicode[STIX]{x1D703},z,t)$
. Figure 8(a–c) exhibits the snapshots for
$u(r,\unicode[STIX]{x1D703},z,t)$
. Figure 8(a–c) exhibits the snapshots for
![]() $Ta=5.0\times 10^{7}$
. It is known, and observed here, that for this Taylor number the coherence length of the dominant flow structures becomes smaller than the gap width
$Ta=5.0\times 10^{7}$
. It is known, and observed here, that for this Taylor number the coherence length of the dominant flow structures becomes smaller than the gap width
![]() $d$
, and turbulence develops in the bulk (Grossmann et al.
Reference Grossmann, Lohse and Sun2016). On the other hand, the boundary layers remain predominantly laminar and as such the regime is referred to as the ‘classical regime’ of TC turbulence. A divergent colour map is chosen to highlight the turbulent structures in the bulk. A snapshot for the smooth inner cylinder simulation is presented in figure 8(a). At
$d$
, and turbulence develops in the bulk (Grossmann et al.
Reference Grossmann, Lohse and Sun2016). On the other hand, the boundary layers remain predominantly laminar and as such the regime is referred to as the ‘classical regime’ of TC turbulence. A divergent colour map is chosen to highlight the turbulent structures in the bulk. A snapshot for the smooth inner cylinder simulation is presented in figure 8(a). At
![]() $z/d\approx 0.3$
, one observes an ejecting structure (plume) that detaches from the inner cylinder laminar boundary layer at the location of an adverse pressure gradient. Locally, where this ejecting plume detaches, the flow will be different (i.e. more chaotic) to that in the other parts of the boundary layer. As such, one also expects the local variables (e.g. skin friction, turbulence intensity) to be different. Later we will therefore employ local averaging, to investigate the spatial differences in the flow associated with this structure (van der Poel et al.
Reference van der Poel, Ostilla-Mónico, Verzicco, Grossmann and Lohse2015b
; Ostilla-Mónico et al.
Reference Ostilla-Mónico, Verzicco, Grossmann and Lohse2016; Zhu et al.
Reference Zhu, Mathai, Stevens, Verzicco and Lohse2018a
). The ejecting and impacting (located at
$z/d\approx 0.3$
, one observes an ejecting structure (plume) that detaches from the inner cylinder laminar boundary layer at the location of an adverse pressure gradient. Locally, where this ejecting plume detaches, the flow will be different (i.e. more chaotic) to that in the other parts of the boundary layer. As such, one also expects the local variables (e.g. skin friction, turbulence intensity) to be different. Later we will therefore employ local averaging, to investigate the spatial differences in the flow associated with this structure (van der Poel et al.
Reference van der Poel, Ostilla-Mónico, Verzicco, Grossmann and Lohse2015b
; Ostilla-Mónico et al.
Reference Ostilla-Mónico, Verzicco, Grossmann and Lohse2016; Zhu et al.
Reference Zhu, Mathai, Stevens, Verzicco and Lohse2018a
). The ejecting and impacting (located at
![]() $z/d\approx 1.3$
) plumes have very strong radial velocity components
$z/d\approx 1.3$
) plumes have very strong radial velocity components
![]() $w$
. From the first term on the right-hand side of (2.8),
$w$
. From the first term on the right-hand side of (2.8),
![]() $r^{3}(\langle w\unicode[STIX]{x1D714}\rangle _{\unicode[STIX]{x1D703},z,t})$
, we then directly see that they strongly contribute to
$r^{3}(\langle w\unicode[STIX]{x1D714}\rangle _{\unicode[STIX]{x1D703},z,t})$
, we then directly see that they strongly contribute to
![]() $Nu_{\unicode[STIX]{x1D714}}$
. This brings us to the remaining (figure 8
b,c) snapshots. Many more, small, plumes are seen to eject from the inner cylinder. The roughness there promotes the detachment of ejecting structures and in that way contributes to a higher
$Nu_{\unicode[STIX]{x1D714}}$
. This brings us to the remaining (figure 8
b,c) snapshots. Many more, small, plumes are seen to eject from the inner cylinder. The roughness there promotes the detachment of ejecting structures and in that way contributes to a higher
![]() $Nu_{\unicode[STIX]{x1D714}}$
. An increase in the level of turbulence, as suggested by the increased level of turbulence dissipation, is quantitatively reflected by a decrease in the Kolmogorov scale (
$Nu_{\unicode[STIX]{x1D714}}$
. An increase in the level of turbulence, as suggested by the increased level of turbulence dissipation, is quantitatively reflected by a decrease in the Kolmogorov scale (
![]() $\unicode[STIX]{x1D702}=(\unicode[STIX]{x1D708}^{3}/\unicode[STIX]{x1D716})^{1/4}$
), namely
$\unicode[STIX]{x1D702}=(\unicode[STIX]{x1D708}^{3}/\unicode[STIX]{x1D716})^{1/4}$
), namely
![]() $\unicode[STIX]{x1D702}/d=7.1\times 10^{-3}$
for the smooth-wall case BS and
$\unicode[STIX]{x1D702}/d=7.1\times 10^{-3}$
for the smooth-wall case BS and
![]() $\unicode[STIX]{x1D702}/d=6.5\times 10^{-3}$
for the highest roughness case B5. Note that the decrease in the Kolmogorov scale
$\unicode[STIX]{x1D702}/d=6.5\times 10^{-3}$
for the highest roughness case B5. Note that the decrease in the Kolmogorov scale
![]() $\unicode[STIX]{x1D702}$
is only small, since
$\unicode[STIX]{x1D702}$
is only small, since
![]() $\unicode[STIX]{x1D702}/d\propto (\unicode[STIX]{x1D716}d^{4}/\unicode[STIX]{x1D708}^{3})^{-1/4}$
. For TC flow, the volume-averaged dissipation rate
$\unicode[STIX]{x1D702}/d\propto (\unicode[STIX]{x1D716}d^{4}/\unicode[STIX]{x1D708}^{3})^{-1/4}$
. For TC flow, the volume-averaged dissipation rate
![]() $\unicode[STIX]{x1D716}$
is related to the angular velocity transport
$\unicode[STIX]{x1D716}$
is related to the angular velocity transport
![]() $Nu_{\unicode[STIX]{x1D714}}$
with:
$Nu_{\unicode[STIX]{x1D714}}$
with:
![]() $\unicode[STIX]{x1D716}=\unicode[STIX]{x1D708}^{3}d^{-4}\unicode[STIX]{x1D70E}^{-2}(Nu_{\unicode[STIX]{x1D714}}-1)Ta+\unicode[STIX]{x1D716}_{lam}$
, where
$\unicode[STIX]{x1D716}=\unicode[STIX]{x1D708}^{3}d^{-4}\unicode[STIX]{x1D70E}^{-2}(Nu_{\unicode[STIX]{x1D714}}-1)Ta+\unicode[STIX]{x1D716}_{lam}$
, where
![]() $\unicode[STIX]{x1D716}_{lam}$
is the laminar volume-averaged dissipation rate,
$\unicode[STIX]{x1D716}_{lam}$
is the laminar volume-averaged dissipation rate,
![]() $d$
is the gap width of the set-up and
$d$
is the gap width of the set-up and
![]() $\unicode[STIX]{x1D70E}=((1+\unicode[STIX]{x1D702})/2/\sqrt{\unicode[STIX]{x1D702}})^{4}$
a geometric parameter (Eckhardt et al.
Reference Eckhardt, Grossmann and Lohse2007). As such, we see that
$\unicode[STIX]{x1D70E}=((1+\unicode[STIX]{x1D702})/2/\sqrt{\unicode[STIX]{x1D702}})^{4}$
a geometric parameter (Eckhardt et al.
Reference Eckhardt, Grossmann and Lohse2007). As such, we see that
![]() $\unicode[STIX]{x1D702}/d\propto Nu_{\unicode[STIX]{x1D714}}^{-1/4}$
only.
$\unicode[STIX]{x1D702}/d\propto Nu_{\unicode[STIX]{x1D714}}^{-1/4}$
only.
Figure 8(d–f) presents snapshots of a flow in the ultimate turbulent state at
![]() $Ta=1.0\times 10^{9}$
(Grossmann et al.
Reference Grossmann, Lohse and Sun2016). Although less pronounced than for
$Ta=1.0\times 10^{9}$
(Grossmann et al.
Reference Grossmann, Lohse and Sun2016). Although less pronounced than for
![]() $Ta=5.0\times 10^{7}$
, we still observe distinct ejecting and impacting regions, indicating the survival of the turbulent Taylor rolls. A similar rationale as applied above, to the classical turbulence case, can also be used to explain the enhancement of the Nusselt number for rough inner cylinders in the ultimate turbulent state. In fact, we can also observe more intense plumes for the highest roughness (D5, figure 8
f), in comparison to a lower roughness case (D2, figure 8
e). Note that here we do not observe the stable vortex formation in between roughness elements and the associated ejection of plumes from sharp peaks, as was reported by Zhu et al. (Reference Zhu, Ostilla-Mónico, Verzicco and Lohse2016) for grooved cylinders, for similar Taylor numbers and roughness heights. The increase in the turbulence level is also quantitatively confirmed by a decrease in the Kolmogorov scale here,
$Ta=5.0\times 10^{7}$
, we still observe distinct ejecting and impacting regions, indicating the survival of the turbulent Taylor rolls. A similar rationale as applied above, to the classical turbulence case, can also be used to explain the enhancement of the Nusselt number for rough inner cylinders in the ultimate turbulent state. In fact, we can also observe more intense plumes for the highest roughness (D5, figure 8
f), in comparison to a lower roughness case (D2, figure 8
e). Note that here we do not observe the stable vortex formation in between roughness elements and the associated ejection of plumes from sharp peaks, as was reported by Zhu et al. (Reference Zhu, Ostilla-Mónico, Verzicco and Lohse2016) for grooved cylinders, for similar Taylor numbers and roughness heights. The increase in the turbulence level is also quantitatively confirmed by a decrease in the Kolmogorov scale here,
![]() $\unicode[STIX]{x1D702}/d=2.7\times 10^{-3}$
for the smooth-wall case DS and
$\unicode[STIX]{x1D702}/d=2.7\times 10^{-3}$
for the smooth-wall case DS and
![]() $\unicode[STIX]{x1D702}/d=2.1\times 10^{-3}$
for the highest roughness case D5.
$\unicode[STIX]{x1D702}/d=2.1\times 10^{-3}$
for the highest roughness case D5.
4.4 Roughness sublayer
The existence of Taylor roll structures is already anticipated in the snapshots of the instantaneous flow in figure 8, from which we observe the ejecting and impacting plume regions. Contour plots of the time and azimuthally averaged azimuthal velocity field, as presented in figure 9, confirm this. Note that the Taylor roll is spatially fixed, allowing for convenient averaging over impacting (solid line), shearing (dashed line) and ejecting (dashed dotted line) regions, a method that we also employed in RB flow (van der Poel et al.
Reference van der Poel, Ostilla-Mónico, Verzicco, Grossmann and Lohse2015b
). For an increasing roughness height, the white region (representing
![]() $\langle u\rangle _{\unicode[STIX]{x1D703},t}\approx 0.5$
) shifts radially outwards and the azimuthal velocity in the bulk increases. This process previously has been seen in Zhu et al. (Reference Zhu, Verschoof, Bakhuis, Huisman, Verzicco, Sun and Lohse2018b
), where it is referred to as the bulk velocity ‘getting slaved to’ to the velocity of a cylinder covered with roughness, reflecting the enhanced drag on the rough side.
$\langle u\rangle _{\unicode[STIX]{x1D703},t}\approx 0.5$
) shifts radially outwards and the azimuthal velocity in the bulk increases. This process previously has been seen in Zhu et al. (Reference Zhu, Verschoof, Bakhuis, Huisman, Verzicco, Sun and Lohse2018b
), where it is referred to as the bulk velocity ‘getting slaved to’ to the velocity of a cylinder covered with roughness, reflecting the enhanced drag on the rough side.
Figure 9. Contour field of the mean azimuthal velocity
![]() $\langle u\rangle _{\unicode[STIX]{x1D703},t}$
in the meridional plane for
$\langle u\rangle _{\unicode[STIX]{x1D703},t}$
in the meridional plane for
![]() $Ta=1.0\times 10^{9}$
. (a) Smooth inner cylinder (DS) (b). Inner cylinder wall roughness
$Ta=1.0\times 10^{9}$
. (a) Smooth inner cylinder (DS) (b). Inner cylinder wall roughness
![]() $k/d=0.0517$
(D2) and (c) inner wall roughness
$k/d=0.0517$
(D2) and (c) inner wall roughness
![]() $k/d=0.0818$
(D5). The solid vertical lines indicate the height of the roughness sublayer
$k/d=0.0818$
(D5). The solid vertical lines indicate the height of the roughness sublayer
![]() $h_{r}$
, calculated over the entire cylinder height.
$h_{r}$
, calculated over the entire cylinder height.

Figure 10. Contour of the time-averaged azimuthal velocity
![]() $\langle u\rangle _{t}^{+}$
, zoomed in on only a few roughness elements, indicated in grey, for
$\langle u\rangle _{t}^{+}$
, zoomed in on only a few roughness elements, indicated in grey, for
![]() $Ta=1.0\times 10^{9}$
(D2). Flow is from left to right. Isolines of
$Ta=1.0\times 10^{9}$
(D2). Flow is from left to right. Isolines of
![]() $\langle u\rangle _{t}^{+}$
overlay the contour. On the vertical axis, we display the wall-normal coordinate normalized by the gap width
$\langle u\rangle _{t}^{+}$
overlay the contour. On the vertical axis, we display the wall-normal coordinate normalized by the gap width
![]() $d$
(left) and in viscous units (right). On the horizontal axis, we display the azimuthal coordinate, normalized by the gap width
$d$
(left) and in viscous units (right). On the horizontal axis, we display the azimuthal coordinate, normalized by the gap width
![]() $d$
(below) and in viscous units (above).
$d$
(below) and in viscous units (above).
Figure 11. (a) Profiles of the root mean square of the form-induced azimuthal velocity fluctuations
![]() $\tilde{u} ^{+}=(\langle u\rangle _{t}-\langle u\rangle _{\unicode[STIX]{x1D703},t})/u_{\unicode[STIX]{x1D70F}}$
at incremental heights above the roughness for identical location and conditions as in figure 9. The radial coordinate
$\tilde{u} ^{+}=(\langle u\rangle _{t}-\langle u\rangle _{\unicode[STIX]{x1D703},t})/u_{\unicode[STIX]{x1D70F}}$
at incremental heights above the roughness for identical location and conditions as in figure 9. The radial coordinate
![]() $r^{+}$
is made dimensionless by the roughness height
$r^{+}$
is made dimensionless by the roughness height
![]() $k^{+}$
. The horizontal axis represents the azimuthal coordinate in viscous units. (b) Root mean squares of the azimuthally averaged form-induced velocity fluctuations. The profiles are obtained at three heights, namely where the Taylor roll impacts, ejects and in the centre (sheared region) – the extent of the regions are estimated from time-averaged velocity fields. The cyan line gives the mean over the entire height of the cylinder. The solid black lines indicate the maximum roughness height
$k^{+}$
. The horizontal axis represents the azimuthal coordinate in viscous units. (b) Root mean squares of the azimuthally averaged form-induced velocity fluctuations. The profiles are obtained at three heights, namely where the Taylor roll impacts, ejects and in the centre (sheared region) – the extent of the regions are estimated from time-averaged velocity fields. The cyan line gives the mean over the entire height of the cylinder. The solid black lines indicate the maximum roughness height
![]() $k_{max}^{+}$
and the height of the roughness sublayer
$k_{max}^{+}$
and the height of the roughness sublayer
![]() $h_{r}^{+}$
.
$h_{r}^{+}$
.
A better impression of the local fluid flow disturbances induced by the roughness elements, is obtained from the time-averaged azimuthal velocity
![]() $\langle u\rangle _{t}$
, a contour of which we show in figure 10. We zoom in on only a few roughness elements and overlay the contour with isolines of
$\langle u\rangle _{t}$
, a contour of which we show in figure 10. We zoom in on only a few roughness elements and overlay the contour with isolines of
![]() $\langle u\rangle _{t}^{+}$
. We observe that local disturbances are limited to a region of only a few times the roughness height, above which the isolines relax to approximate horizontal lines. We observe small recirculation zones (closed isolines) in open regions behind high roughness elements. To quantify the degree of roughness-induced velocity disturbance, we apply a triple decomposition to the instantaneous azimuthal velocity
$\langle u\rangle _{t}^{+}$
. We observe that local disturbances are limited to a region of only a few times the roughness height, above which the isolines relax to approximate horizontal lines. We observe small recirculation zones (closed isolines) in open regions behind high roughness elements. To quantify the degree of roughness-induced velocity disturbance, we apply a triple decomposition to the instantaneous azimuthal velocity
![]() $u(r,\unicode[STIX]{x1D703},z,t)$
(Pokrajac et al.
Reference Pokrajac, Campbell, Nikora, Manes and McEwan2007),
$u(r,\unicode[STIX]{x1D703},z,t)$
(Pokrajac et al.
Reference Pokrajac, Campbell, Nikora, Manes and McEwan2007),
where
![]() $u^{\prime }(r,\unicode[STIX]{x1D703},z,t)=u(r,\unicode[STIX]{x1D703},z,t)-\langle u\rangle _{t}(r,\unicode[STIX]{x1D703},z)$
, the temporal fluctuation and
$u^{\prime }(r,\unicode[STIX]{x1D703},z,t)=u(r,\unicode[STIX]{x1D703},z,t)-\langle u\rangle _{t}(r,\unicode[STIX]{x1D703},z)$
, the temporal fluctuation and
![]() $\tilde{u} (r,\unicode[STIX]{x1D703},z)=\langle u\rangle _{t}(r,\unicode[STIX]{x1D703},z)-\langle u\rangle _{\unicode[STIX]{x1D703},t}(r,z)$
, the component that is strongly related to the roughness induced disturbances and therefore termed the form-induced (or dispersive) velocity fluctuation. Note that by applying the triple decomposition to the full NS equations and then averaging in
$\tilde{u} (r,\unicode[STIX]{x1D703},z)=\langle u\rangle _{t}(r,\unicode[STIX]{x1D703},z)-\langle u\rangle _{\unicode[STIX]{x1D703},t}(r,z)$
, the component that is strongly related to the roughness induced disturbances and therefore termed the form-induced (or dispersive) velocity fluctuation. Note that by applying the triple decomposition to the full NS equations and then averaging in
![]() $\unicode[STIX]{x1D703}$
and
$\unicode[STIX]{x1D703}$
and
![]() $t$
, one will recover the related form-induced stress tensor
$t$
, one will recover the related form-induced stress tensor
![]() $\langle \tilde{u} _{i}\tilde{u} _{j}\rangle _{\unicode[STIX]{x1D703},t}$
. However, here we only discuss
$\langle \tilde{u} _{i}\tilde{u} _{j}\rangle _{\unicode[STIX]{x1D703},t}$
. However, here we only discuss
![]() $\tilde{u} (r,\unicode[STIX]{x1D703},z)$
. The root mean square of the form-induced fluctuations
$\tilde{u} (r,\unicode[STIX]{x1D703},z)$
. The root mean square of the form-induced fluctuations
![]() $\sqrt{\tilde{u} (r,\unicode[STIX]{x1D703},z)^{2}}^{+}$
at various heights above the roughness is given in figure 11(a). The horizontal axis corresponds to the roughness elements shown in figure 10. Already for
$\sqrt{\tilde{u} (r,\unicode[STIX]{x1D703},z)^{2}}^{+}$
at various heights above the roughness is given in figure 11(a). The horizontal axis corresponds to the roughness elements shown in figure 10. Already for
![]() $r/k=4.5$
(with
$r/k=4.5$
(with
![]() $k$
being the roughness height, i.e. the smallest radius of the ellipsoidal building block) we find it hard to detect spatial fluctuations along
$k$
being the roughness height, i.e. the smallest radius of the ellipsoidal building block) we find it hard to detect spatial fluctuations along
![]() $\unicode[STIX]{x1D703}$
. For
$\unicode[STIX]{x1D703}$
. For
![]() $r/k=12.0$
, the line is barely distinguishable from the horizontal axis. If we average the lines over the azimuthal direction, we obtain the behaviour of the dispersive fluctations as a function of the wall-normal distance; see figure 11(b). We plot the lines for three respective axial locations, that is the impacting, sheared and ejecting regions, and find little variance in the wall-normal extent of the form-induced fluctuations, for the varying locations. The vertical black line represent the maximum roughness height, below which we average only over fluid regions.
$r/k=12.0$
, the line is barely distinguishable from the horizontal axis. If we average the lines over the azimuthal direction, we obtain the behaviour of the dispersive fluctations as a function of the wall-normal distance; see figure 11(b). We plot the lines for three respective axial locations, that is the impacting, sheared and ejecting regions, and find little variance in the wall-normal extent of the form-induced fluctuations, for the varying locations. The vertical black line represent the maximum roughness height, below which we average only over fluid regions.
Rough elements on the inner cylinder destroy the streamwise homogeneity of the flow, and thus the root mean square of the dispersive fluctuation is non-zero. Some distance from the wall, the turbulence is well able to ‘mix out’ the form-induced structures and the flow regains streamwise homogeneity. The distance from the wall at which the dispersive fluctuations are zero (or reasonably close to zero), is called the roughness sublayer height
![]() $h_{r}$
. In this research, we define
$h_{r}$
. In this research, we define
![]() $y^{+}=h_{r}^{+}$
where
$y^{+}=h_{r}^{+}$
where
![]() $\sqrt{\langle \tilde{u} ^{+2}\rangle _{\unicode[STIX]{x1D703},z}}(r)=0.01\langle u^{+}\rangle _{\unicode[STIX]{x1D703},z,t}$
and find
$\sqrt{\langle \tilde{u} ^{+2}\rangle _{\unicode[STIX]{x1D703},z}}(r)=0.01\langle u^{+}\rangle _{\unicode[STIX]{x1D703},z,t}$
and find
![]() $h_{r}=3.70k$
(
$h_{r}=3.70k$
(
![]() $h_{r}=2.78k_{s}$
). This value agrees well with a roughness sublayer height of
$h_{r}=2.78k_{s}$
). This value agrees well with a roughness sublayer height of
![]() $2\lesssim k_{s}\lesssim 5$
, as typically found in other canonical flows (Pokrajac et al.
Reference Pokrajac, Campbell, Nikora, Manes and McEwan2007).
$2\lesssim k_{s}\lesssim 5$
, as typically found in other canonical flows (Pokrajac et al.
Reference Pokrajac, Campbell, Nikora, Manes and McEwan2007).
The existence of a finite height of only a few times the roughness height, at which the dynamical effects of the roughness on the fluid flow vanish, is an important finding in wall-bounded turbulence. As written in Flack & Schultz (Reference Flack and Schultz2014): ‘...the utility of the roughness function itself hinges on similarity of the flow’. This idea (‘wall similarity’) is already heavily tested in other systems (Raupach et al. Reference Raupach, Antonia and Rajagopalan1991; Chung, Monty & Ooi Reference Chung, Monty and Ooi2014; Flack & Schultz Reference Flack and Schultz2014) and in the vast majority of the research found to be correct. However, in a heavily stratified system as TC, where wall-attached structures result from the unstable stratification of centrifugal pressure, the notion of wall similarity is not yet investigated. As such, the findings presented here, that such similarity exists in TC, strengthen our believe that TC could be a valued system to characterize the equivalent sand grain roughness height of a given rough surface.
4.5 Radial profiles
The effects of roughness on a turbulent shear-driven flow, where the shear rate is constant, can be separated into two effects. The first is the change in the wall shear stress
![]() $\unicode[STIX]{x1D70F}_{w}$
. The second is the change in the structure of the turbulent flow at a given wall shear stress. Sand grains increase
$\unicode[STIX]{x1D70F}_{w}$
. The second is the change in the structure of the turbulent flow at a given wall shear stress. Sand grains increase
![]() $\unicode[STIX]{x1D70F}_{w}$
and therefore we find an increased momentum transfer to the bulk region with respect to a smooth-wall TC case, at fixed Taylor number. This increased momentum transfer to the bulk (through plumes, very similar to Rayleigh–Bénard flow) leads to a more intense turbulence in the bulk flow, and also to higher velocity fluctuations.
$\unicode[STIX]{x1D70F}_{w}$
and therefore we find an increased momentum transfer to the bulk region with respect to a smooth-wall TC case, at fixed Taylor number. This increased momentum transfer to the bulk (through plumes, very similar to Rayleigh–Bénard flow) leads to a more intense turbulence in the bulk flow, and also to higher velocity fluctuations.
We plot the time and azimuthally averaged azimuthal velocity for
![]() $Ta=5.0\times 10^{8}$
in figure 12(a). The roughness covers the inner cylinder, i.e.
$Ta=5.0\times 10^{8}$
in figure 12(a). The roughness covers the inner cylinder, i.e.
![]() $(r-r_{i})/d\leqslant 0.07$
. In this section we focus on the behaviour of the statistics above the roughness. Therefore, averaging over both solid and fluid regions is carried out. For increasing roughness height, see the legend for viscous roughness heights, the azimuthal velocity in the bulk increases. Figure 12(b) then presents the corresponding azimuthal velocity profiles for constant
$(r-r_{i})/d\leqslant 0.07$
. In this section we focus on the behaviour of the statistics above the roughness. Therefore, averaging over both solid and fluid regions is carried out. For increasing roughness height, see the legend for viscous roughness heights, the azimuthal velocity in the bulk increases. Figure 12(b) then presents the corresponding azimuthal velocity profiles for constant
![]() $k/d=0.060\pm 0.002$
and varying Taylor number.
$k/d=0.060\pm 0.002$
and varying Taylor number.
Figure 13(a) shows the double-averaged radial profiles
![]() $(u)_{rms}^{+}=\langle \langle u^{2}\rangle _{\unicode[STIX]{x1D703},z,t}-\langle u\rangle _{\unicode[STIX]{x1D703},z,t}^{2}\rangle ^{1/2}/u_{\unicode[STIX]{x1D70F}}$
for constant Taylor number
$(u)_{rms}^{+}=\langle \langle u^{2}\rangle _{\unicode[STIX]{x1D703},z,t}-\langle u\rangle _{\unicode[STIX]{x1D703},z,t}^{2}\rangle ^{1/2}/u_{\unicode[STIX]{x1D70F}}$
for constant Taylor number
![]() $Ta=1.0\times 10^{9}$
. For the smooth-wall case, the peak of
$Ta=1.0\times 10^{9}$
. For the smooth-wall case, the peak of
![]() $(u^{+})_{rms}$
is located at
$(u^{+})_{rms}$
is located at
![]() $y^{+}\approx 10$
. This agrees with the smooth case in (Ostilla-Mónico et al.
Reference Ostilla-Mónico, Verzicco, Grossmann and Lohse2016) for TC flow, but is closer to the solid boundary than is found in channel flow;
$y^{+}\approx 10$
. This agrees with the smooth case in (Ostilla-Mónico et al.
Reference Ostilla-Mónico, Verzicco, Grossmann and Lohse2016) for TC flow, but is closer to the solid boundary than is found in channel flow;
![]() $y^{+}\approx 12$
. We observe a slight decrease in the viscous scaled turbulence intensity
$y^{+}\approx 12$
. We observe a slight decrease in the viscous scaled turbulence intensity
![]() $(u)_{rms}^{+}$
for increasing roughness heights, close to the inner cylinder. Further outside the profiles, the profiles collapse.
$(u)_{rms}^{+}$
for increasing roughness heights, close to the inner cylinder. Further outside the profiles, the profiles collapse.

Figure 12. Profiles of the mean streamwise velocity
![]() $\langle u\rangle _{\unicode[STIX]{x1D703},z,t}$
versus the radial coordinate
$\langle u\rangle _{\unicode[STIX]{x1D703},z,t}$
versus the radial coordinate
![]() $(r-r_{i})/d$
, where
$(r-r_{i})/d$
, where
![]() $r_{i}$
is the radius of the inner cylinder and
$r_{i}$
is the radius of the inner cylinder and
![]() $d$
is the gap width. (a) Constant Taylor number
$d$
is the gap width. (a) Constant Taylor number
![]() $Ta=5.0\times 10^{8}$
and increasing roughness heights. The profiles exhibit clear ‘slaving’, i.e. the bulk velocity moves towards the velocity of the roughened cylinder. (b) Constant roughness height
$Ta=5.0\times 10^{8}$
and increasing roughness heights. The profiles exhibit clear ‘slaving’, i.e. the bulk velocity moves towards the velocity of the roughened cylinder. (b) Constant roughness height
![]() $k/d=0.060\pm 0.002$
for increasing Taylor number. Increased slaving of the bulk velocity is observed for increasing viscous scaled roughness height
$k/d=0.060\pm 0.002$
for increasing Taylor number. Increased slaving of the bulk velocity is observed for increasing viscous scaled roughness height
![]() $k_{s}^{+}$
, respectively: (blue)
$k_{s}^{+}$
, respectively: (blue)
![]() $k_{s}^{+}=9$
, (green)
$k_{s}^{+}=9$
, (green)
![]() $k_{s}^{+}=24$
, (red)
$k_{s}^{+}=24$
, (red)
![]() $k_{s}^{+}=47$
and (cyan)
$k_{s}^{+}=47$
and (cyan)
![]() $k_{s}^{+}=65$
.
$k_{s}^{+}=65$
.
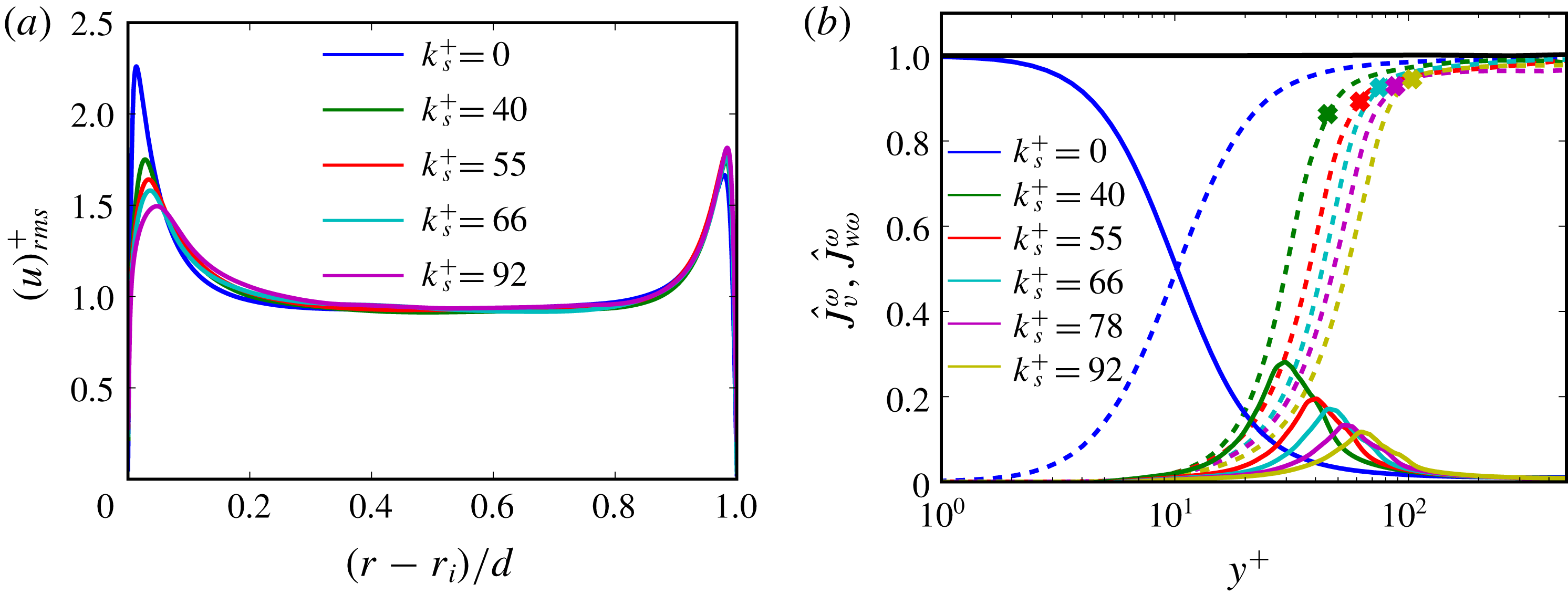
Figure 13. (a) Root mean square of the mean streamwise velocity
![]() $(u)_{rms}^{+}=\langle \langle u^{2}\rangle _{\unicode[STIX]{x1D703},z,t}-\langle u\rangle _{\unicode[STIX]{x1D703},z,t}^{2}\rangle ^{1/2}/u_{\unicode[STIX]{x1D70F}}$
versus the radius
$(u)_{rms}^{+}=\langle \langle u^{2}\rangle _{\unicode[STIX]{x1D703},z,t}-\langle u\rangle _{\unicode[STIX]{x1D703},z,t}^{2}\rangle ^{1/2}/u_{\unicode[STIX]{x1D70F}}$
versus the radius
![]() $(r-r_{i})/d$
for
$(r-r_{i})/d$
for
![]() $Ta=1.0\times 10^{9}$
. We observe an overall decrease of the viscous scaled turbulence intensity for increasing roughness height
$Ta=1.0\times 10^{9}$
. We observe an overall decrease of the viscous scaled turbulence intensity for increasing roughness height
![]() $k_{s}^{+}$
. (b) The viscous
$k_{s}^{+}$
. (b) The viscous
![]() ${\hat{J}}_{\unicode[STIX]{x1D708}}^{\unicode[STIX]{x1D714}}(y^{+})\equiv -r^{3}\unicode[STIX]{x1D708}\unicode[STIX]{x2202}_{r}\langle \unicode[STIX]{x1D714}\rangle _{\unicode[STIX]{x1D703},z,t}/J_{\unicode[STIX]{x1D708}}^{\unicode[STIX]{x1D714}}(r_{o})$
(solid line) and Reynolds stress
${\hat{J}}_{\unicode[STIX]{x1D708}}^{\unicode[STIX]{x1D714}}(y^{+})\equiv -r^{3}\unicode[STIX]{x1D708}\unicode[STIX]{x2202}_{r}\langle \unicode[STIX]{x1D714}\rangle _{\unicode[STIX]{x1D703},z,t}/J_{\unicode[STIX]{x1D708}}^{\unicode[STIX]{x1D714}}(r_{o})$
(solid line) and Reynolds stress
![]() ${\hat{J}}_{w\unicode[STIX]{x1D714}}^{\unicode[STIX]{x1D714}}(y^{+})\equiv r^{3}\langle w\unicode[STIX]{x1D714}\rangle _{\unicode[STIX]{x1D703},z,t}/J_{\unicode[STIX]{x1D708}}^{\unicode[STIX]{x1D714}}(r_{o})$
(dashed line) terms of the conserved angular velocity flux
${\hat{J}}_{w\unicode[STIX]{x1D714}}^{\unicode[STIX]{x1D714}}(y^{+})\equiv r^{3}\langle w\unicode[STIX]{x1D714}\rangle _{\unicode[STIX]{x1D703},z,t}/J_{\unicode[STIX]{x1D708}}^{\unicode[STIX]{x1D714}}(r_{o})$
(dashed line) terms of the conserved angular velocity flux
![]() ${\hat{J}}^{\unicode[STIX]{x1D714}}$
versus the wall-normal distance
${\hat{J}}^{\unicode[STIX]{x1D714}}$
versus the wall-normal distance
![]() $y^{+}$
for
$y^{+}$
for
![]() $Ta=1.0\times 10^{9}$
. The sum of the individual terms represents the total conserved angular velocity flux radially outwards. The black horizontal line at
$Ta=1.0\times 10^{9}$
. The sum of the individual terms represents the total conserved angular velocity flux radially outwards. The black horizontal line at
![]() ${\hat{J}}^{\unicode[STIX]{x1D714}}=1.0$
is the sum of the two blue lines for the smooth-wall case. It is observed that
${\hat{J}}^{\unicode[STIX]{x1D714}}=1.0$
is the sum of the two blue lines for the smooth-wall case. It is observed that
![]() ${\hat{J}}^{\unicode[STIX]{x1D714}}$
is conserved above the maximum roughness height (indicated by cross markers).
${\hat{J}}^{\unicode[STIX]{x1D714}}$
is conserved above the maximum roughness height (indicated by cross markers).
The reason why we choose to make the variables dimensionless using their friction equivalents is to assess those changes to the flow that go beyond the effects coming from ‘simply’ increasing the momentum input to that region, i.e. to study the structural changes of the turbulent flow for the same momentum input. We can thus infer from figure 13(a) that the bulk of the TC flow is not affected by the roughness elements, other than increasing the momentum input into the bulk would do. A gedankenexperiment (see e.g. Chung et al. (Reference Chung, Monty and Ooi2014)) would make this clear. If one would be placed into the bulk of a rough TC flow, without being able to look into the boundary layer, one could not tell whether the wall is rough or smooth. The reason is that a smooth wall with a higher Taylor number can produce the same
![]() $\unicode[STIX]{x1D70F}_{w}$
as a rough wall with a lower Taylor number. This idea is, in fact, Townsend’s outer layer similarity hypothesis (Townsend Reference Townsend1956). (Note: we can only be sure that this holds for the relatively small sand grain surface under scrutiny here, owing to the sufficient scale separation!) As such, we conclude that the influence of the roughness elements pertains only to a region close to the wall.
$\unicode[STIX]{x1D70F}_{w}$
as a rough wall with a lower Taylor number. This idea is, in fact, Townsend’s outer layer similarity hypothesis (Townsend Reference Townsend1956). (Note: we can only be sure that this holds for the relatively small sand grain surface under scrutiny here, owing to the sufficient scale separation!) As such, we conclude that the influence of the roughness elements pertains only to a region close to the wall.
It has already been mentioned that the angular velocity flux
![]() $J^{\unicode[STIX]{x1D714}}(y^{+})$
is conserved in the radial direction, see § 4.2. However, the individual components – i.e. the viscous
$J^{\unicode[STIX]{x1D714}}(y^{+})$
is conserved in the radial direction, see § 4.2. However, the individual components – i.e. the viscous
![]() $J_{\unicode[STIX]{x1D708}}^{\unicode[STIX]{x1D714}}(y^{+})$
and Reynolds stress
$J_{\unicode[STIX]{x1D708}}^{\unicode[STIX]{x1D714}}(y^{+})$
and Reynolds stress
![]() $J_{w\unicode[STIX]{x1D714}}^{\unicode[STIX]{x1D714}}(y^{+})$
terms – are functions of the wall-normal (radial) coordinate. The profiles of these terms are shown in figure 13(b). We normalize all terms with
$J_{w\unicode[STIX]{x1D714}}^{\unicode[STIX]{x1D714}}(y^{+})$
terms – are functions of the wall-normal (radial) coordinate. The profiles of these terms are shown in figure 13(b). We normalize all terms with
![]() $J_{\unicode[STIX]{x1D708}}^{\unicode[STIX]{x1D714}}(r_{o})$
. The viscous stress terms are presented as solid lines and the Reynolds stress terms as dashed lines. The blue lines represent the smooth-wall case. Very close to the inner cylinder (
$J_{\unicode[STIX]{x1D708}}^{\unicode[STIX]{x1D714}}(r_{o})$
. The viscous stress terms are presented as solid lines and the Reynolds stress terms as dashed lines. The blue lines represent the smooth-wall case. Very close to the inner cylinder (
![]() $y^{+}=1$
),
$y^{+}=1$
),
![]() $J^{\unicode[STIX]{x1D714}}\approx J_{\unicode[STIX]{x1D708}}^{\unicode[STIX]{x1D714}}$
; this is expected, since there the gradient of the mean streamwise velocity is maximum and the wall-normal component of the velocity vector goes to zero. On the far right of figure 13(b), the gradient of the mean velocity approaches zero in the bulk, and the correlation function between the wall-normal and angular velocity goes to a maximum; as such
$J^{\unicode[STIX]{x1D714}}\approx J_{\unicode[STIX]{x1D708}}^{\unicode[STIX]{x1D714}}$
; this is expected, since there the gradient of the mean streamwise velocity is maximum and the wall-normal component of the velocity vector goes to zero. On the far right of figure 13(b), the gradient of the mean velocity approaches zero in the bulk, and the correlation function between the wall-normal and angular velocity goes to a maximum; as such
![]() $J^{\unicode[STIX]{x1D714}}\approx J_{w\unicode[STIX]{x1D714}}^{\unicode[STIX]{x1D714}}$
. The black line represents the sum of the viscous and Reynold stress terms, for the smooth (blue) case, and is independent of
$J^{\unicode[STIX]{x1D714}}\approx J_{w\unicode[STIX]{x1D714}}^{\unicode[STIX]{x1D714}}$
. The black line represents the sum of the viscous and Reynold stress terms, for the smooth (blue) case, and is independent of
![]() $y^{+}$
. The situation for the rough cylinder cases is more complex. For increasing roughness height, the viscous stress reaches a maximum below the maximum roughness height. This can be explained by the recirculation zones behind the roughness elements. Then, above the roughness, the viscous stress goes to zero in the bulk. For the Reynolds stress terms the increase is monotonic, and similar to the smooth-wall case. However, we observe a steeper increase for the rough cases. Note that under the maximum roughness height, the viscous and Reynolds stress terms do not add up to unity, since the rough surface acts as a radial dependent momentum source term to the NS equations there.
$y^{+}$
. The situation for the rough cylinder cases is more complex. For increasing roughness height, the viscous stress reaches a maximum below the maximum roughness height. This can be explained by the recirculation zones behind the roughness elements. Then, above the roughness, the viscous stress goes to zero in the bulk. For the Reynolds stress terms the increase is monotonic, and similar to the smooth-wall case. However, we observe a steeper increase for the rough cases. Note that under the maximum roughness height, the viscous and Reynolds stress terms do not add up to unity, since the rough surface acts as a radial dependent momentum source term to the NS equations there.
5 Summary and conclusions
We have performed direct numerical simulations of turbulent Taylor–Couette flow with inner cylinder rotation and inner cylinder sand grain roughness. The Taylor number ranges from
![]() $Ta=1.0\times 10^{7}$
(
$Ta=1.0\times 10^{7}$
(
![]() $Re_{\unicode[STIX]{x1D70F}}=82$
) up to
$Re_{\unicode[STIX]{x1D70F}}=82$
) up to
![]() $Ta=1.0\times 10^{9}$
(
$Ta=1.0\times 10^{9}$
(
![]() $Re_{\unicode[STIX]{x1D70F}}=635$
), covering thereby both the classical and the ultimate regimes of turbulent TC flow. In particular, we studied the effects of the roughness height on the fluid flow in the transitionally rough and fully rough regimes, with the equivalent sand grain roughness height ranging from
$Re_{\unicode[STIX]{x1D70F}}=635$
), covering thereby both the classical and the ultimate regimes of turbulent TC flow. In particular, we studied the effects of the roughness height on the fluid flow in the transitionally rough and fully rough regimes, with the equivalent sand grain roughness height ranging from
![]() $k_{s}^{+}=5$
to
$k_{s}^{+}=5$
to
![]() $k_{s}^{+}=92$
. We modelled the sand grains as randomly rotated and translated ellipsoids of constant size and shape (monodisperse), similar to the model proposed by Scotti (Reference Scotti2006). The surface was implemented into a second-order finite difference code by means of the immersed boundary method.
$k_{s}^{+}=92$
. We modelled the sand grains as randomly rotated and translated ellipsoids of constant size and shape (monodisperse), similar to the model proposed by Scotti (Reference Scotti2006). The surface was implemented into a second-order finite difference code by means of the immersed boundary method.
We confirm an increase in the dimensionless torque, expressed as the Nusselt number, for increasing roughness height. This is attributed to the enhanced boundary layer detachment, resulting in plume ejection regions, which we observed in snapshots of the azimuthal velocity field. The plumes contain a strong radial velocity component, and as such contribute strongly to the Reynolds stress term of the angular velocity flux. This mechanism is analogous to what was found for the Nu increase for grooved TC turbulence by Zhu et al. (Reference Zhu, Ostilla-Mónico, Verzicco and Lohse2016).
To quantify the degree of roughness-induced disturbance to the velocity field, we measured the dispersive fluctuations of the azimuthal velocity component,
![]() $\tilde{u} =\langle u\rangle _{t}-\langle u\rangle _{\unicode[STIX]{x1D703},t}$
. This dispersive term was obtained by means of a triple decomposition to the azimuthal velocity. We defined the height of the roughness sublayer
$\tilde{u} =\langle u\rangle _{t}-\langle u\rangle _{\unicode[STIX]{x1D703},t}$
. This dispersive term was obtained by means of a triple decomposition to the azimuthal velocity. We defined the height of the roughness sublayer
![]() $h_{r}$
there where the dispersive fluctuations become very small, such that
$h_{r}$
there where the dispersive fluctuations become very small, such that
![]() $\sqrt{\langle \tilde{u} ^{+2}\rangle _{\unicode[STIX]{x1D703},z}}=0.01\langle u^{+}\rangle _{\unicode[STIX]{x1D703},z,t}$
and found the height of the roughness sublayer to be
$\sqrt{\langle \tilde{u} ^{+2}\rangle _{\unicode[STIX]{x1D703},z}}=0.01\langle u^{+}\rangle _{\unicode[STIX]{x1D703},z,t}$
and found the height of the roughness sublayer to be
![]() $h_{r}=2.78k_{s}$
. This height of the roughness sublayer compares well with values found for other canonical systems (Pokrajac et al.
Reference Pokrajac, Campbell, Nikora, Manes and McEwan2007). The low height of the roughness sublayer in TC flow, and the existence of similarity of the flow above this sublayer, leads us to believe that we can utilize the shift of the logarithmic region to find an equivalent sand grain roughness height.
$h_{r}=2.78k_{s}$
. This height of the roughness sublayer compares well with values found for other canonical systems (Pokrajac et al.
Reference Pokrajac, Campbell, Nikora, Manes and McEwan2007). The low height of the roughness sublayer in TC flow, and the existence of similarity of the flow above this sublayer, leads us to believe that we can utilize the shift of the logarithmic region to find an equivalent sand grain roughness height.
The hallmark of turbulent flows over rough walls is the shift of the logarithmic streamwise velocity profile
![]() $\unicode[STIX]{x0394}u^{+}$
. The shift is a function of any parameters describing the roughness topology. Here we focused in particular on the effect of the sand grain size
$\unicode[STIX]{x0394}u^{+}$
. The shift is a function of any parameters describing the roughness topology. Here we focused in particular on the effect of the sand grain size
![]() $k$
and the roughness function becomes
$k$
and the roughness function becomes
![]() $\unicode[STIX]{x0394}u^{+}(k^{+})$
. It was shown in Huisman et al. (Reference Huisman, Scharnowski, Cierpka, Kähler, Lohse and Sun2013) that the constants of the logarithmic law are not constant in the Taylor number range of our simulations. Hence we proposed the generalization
$\unicode[STIX]{x0394}u^{+}(k^{+})$
. It was shown in Huisman et al. (Reference Huisman, Scharnowski, Cierpka, Kähler, Lohse and Sun2013) that the constants of the logarithmic law are not constant in the Taylor number range of our simulations. Hence we proposed the generalization
![]() $u^{+}=f_{1}(Re_{i})\log (y^{+})+f_{2}(Re_{i})-\unicode[STIX]{x0394}u^{+}$
.
$u^{+}=f_{1}(Re_{i})\log (y^{+})+f_{2}(Re_{i})-\unicode[STIX]{x0394}u^{+}$
.
We performed simulations at four Ta and various roughness heights and ensured that the
![]() $k^{+}$
range for the various Ta numbers overlaps. First, we concluded that the velocity shift is independent of Ta, despite the Ta dependence of the constant in the logarithmic layer. As such, all simulations collapse onto a single curve. Second, we saw a strong overlap between the roughness function calculated from our DNS in TC flow and the seminal work by Nikuradse (Reference Nikuradse1933) on monodisperse sand grains in pipe flow, in the transitionally rough regime. We found
$k^{+}$
range for the various Ta numbers overlaps. First, we concluded that the velocity shift is independent of Ta, despite the Ta dependence of the constant in the logarithmic layer. As such, all simulations collapse onto a single curve. Second, we saw a strong overlap between the roughness function calculated from our DNS in TC flow and the seminal work by Nikuradse (Reference Nikuradse1933) on monodisperse sand grains in pipe flow, in the transitionally rough regime. We found
![]() $k_{s}^{+}=1.33k$
. Only for very low
$k_{s}^{+}=1.33k$
. Only for very low
![]() $k_{s}^{+}$
values, close to the hydrodynamically smooth regime, we found that the simulations slightly differ from the Nikuradse curve.
$k_{s}^{+}$
values, close to the hydrodynamically smooth regime, we found that the simulations slightly differ from the Nikuradse curve.
It is remarkable that the Hama roughness function appears to be universal for similar surfaces in such different systems. Note in particular that we have a streamwise curvature and strong secondary motions (Taylor rolls), which were absent in the pipe flow experiments of Nikuradse. As such, our findings point towards a universal behaviour of the roughness function for very different fluid flow systems. However, many more comparison studies, of identical rough surfaces and varying fluid flow systems, are needed to confirm this notion.
Acknowledgements
We wish to express our gratitude to J. Will for his help with various illustrations. This project is funded by the Priority Programme SPP 1881 Turbulent Superstructures of the Deutsche Forschungsgemeinschaft. We also acknowledge PRACE for awarding us access to Marconi, based in Italy at CINECA under PRACE project number 2016143351. We also acknowledge PRACE for awarding us access to MareNostrum based in Spain at the Barcelona Supercomputing Centre (BSC) under PRACE project number 2017174146. This work was partly carried out on the national e-infrastructure of SURFsara, a subsidiary of SURF cooperation, the collaborative ICT organization for Dutch education and research.
Appendix
Table 2. Parameters describing the surface geometry (including both blank patches and sand grains). From left to right: case number in accordance with table 1. The roughness height is measured with respect to the inner cylinder location
![]() $r=r_{0}$
.
$r=r_{0}$
.
![]() $\bar{k}/k_{max}$
is the mean roughness height respective to the maximum roughness height.
$\bar{k}/k_{max}$
is the mean roughness height respective to the maximum roughness height.
![]() $\bar{k}$
is the first moment of the roughness height distribution,
$\bar{k}$
is the first moment of the roughness height distribution,
![]() $1/S\int _{S}h(\unicode[STIX]{x1D703},z)\,\text{d}S$
.
$1/S\int _{S}h(\unicode[STIX]{x1D703},z)\,\text{d}S$
.
![]() $k_{std}$
is the standard deviation of the surface height distribution
$k_{std}$
is the standard deviation of the surface height distribution
![]() $(1/S\int _{S}(h(\unicode[STIX]{x1D703},z)-\bar{k})^{2}\,\text{d}S)^{1/2}$
,
$(1/S\int _{S}(h(\unicode[STIX]{x1D703},z)-\bar{k})^{2}\,\text{d}S)^{1/2}$
,
![]() $Sk$
is the skewness
$Sk$
is the skewness
![]() $1/k_{std}^{3}S\int _{S}(h(\unicode[STIX]{x1D703},z)-\bar{k})^{3}\,\text{d}S$
and
$1/k_{std}^{3}S\int _{S}(h(\unicode[STIX]{x1D703},z)-\bar{k})^{3}\,\text{d}S$
and
![]() $Ku$
the excess kurtosis,
$Ku$
the excess kurtosis,
![]() $1/k_{std}^{4}S\int _{S}(h(\unicode[STIX]{x1D703},z)-\bar{k})^{4}\,\text{d}S-3$
.
$1/k_{std}^{4}S\int _{S}(h(\unicode[STIX]{x1D703},z)-\bar{k})^{4}\,\text{d}S-3$
.
![]() $k_{rms}$
is the root mean square of the mean height
$k_{rms}$
is the root mean square of the mean height
![]() $(1/S\int _{S}(h(\unicode[STIX]{x1D703},z))^{2}\,\text{d}S)^{1/2}$
.
$(1/S\int _{S}(h(\unicode[STIX]{x1D703},z))^{2}\,\text{d}S)^{1/2}$
.
![]() $k_{p}$
is the mean peak height. The peaks are obtained by a peak finding algorithm (‘find_peak_local’ in van der Walt et al. (Reference van der Walt, Schönberger, Nunez-Iglesias, Boulogne, Warner, Yager, Gouillart and Yu2014)) with zero threshold and a minimum spacing of the peaks of four grid nodes.
$k_{p}$
is the mean peak height. The peaks are obtained by a peak finding algorithm (‘find_peak_local’ in van der Walt et al. (Reference van der Walt, Schönberger, Nunez-Iglesias, Boulogne, Warner, Yager, Gouillart and Yu2014)) with zero threshold and a minimum spacing of the peaks of four grid nodes.
![]() $ES$
is the effective slope,
$ES$
is the effective slope,
![]() $ES=1/L_{\unicode[STIX]{x1D703}}L_{z}\int _{L_{\unicode[STIX]{x1D703}}}\int _{L_{z}}|\unicode[STIX]{x2202}h(\unicode[STIX]{x1D703},z)/\unicode[STIX]{x2202}(r_{i}\unicode[STIX]{x1D703})|\,\text{d}z\,\text{d}(r_{i}\unicode[STIX]{x1D703})$
as introduced by Napoli et al. (Reference Napoli, Armenio and De Marchis2008). It can be shown that the
$ES=1/L_{\unicode[STIX]{x1D703}}L_{z}\int _{L_{\unicode[STIX]{x1D703}}}\int _{L_{z}}|\unicode[STIX]{x2202}h(\unicode[STIX]{x1D703},z)/\unicode[STIX]{x2202}(r_{i}\unicode[STIX]{x1D703})|\,\text{d}z\,\text{d}(r_{i}\unicode[STIX]{x1D703})$
as introduced by Napoli et al. (Reference Napoli, Armenio and De Marchis2008). It can be shown that the
![]() $ES$
parameter is twice the often used solidity parameter
$ES$
parameter is twice the often used solidity parameter
![]() $\unicode[STIX]{x1D706}$
(Jiménez Reference Jiménez2004).
$\unicode[STIX]{x1D706}$
(Jiménez Reference Jiménez2004).
![]() $\unicode[STIX]{x1D6FC}$
is the surface gradient in the streamwise direction,
$\unicode[STIX]{x1D6FC}$
is the surface gradient in the streamwise direction,
![]() $\unicode[STIX]{x2202}h(\unicode[STIX]{x1D703},z)/\unicode[STIX]{x2202}r_{i}\unicode[STIX]{x1D703}$
and
$\unicode[STIX]{x2202}h(\unicode[STIX]{x1D703},z)/\unicode[STIX]{x2202}r_{i}\unicode[STIX]{x1D703}$
and
![]() $\unicode[STIX]{x1D6FC}_{rms}$
is the root mean square of this distribution.
$\unicode[STIX]{x1D6FC}_{rms}$
is the root mean square of this distribution.
![]() $S_{f}$
is the total frontal projected area of the roughness (in the streamwise direction).
$S_{f}$
is the total frontal projected area of the roughness (in the streamwise direction).
![]() $S_{s}$
is the total windward wetted area of the roughness.
$S_{s}$
is the total windward wetted area of the roughness.
![]() $\unicode[STIX]{x1D6EC}$
is the density parameter which relates the latter two parameters by
$\unicode[STIX]{x1D6EC}$
is the density parameter which relates the latter two parameters by
![]() $\unicode[STIX]{x1D6EC}=(S/S_{f})(S_{f}/S_{s})^{-1.6}$
where
$\unicode[STIX]{x1D6EC}=(S/S_{f})(S_{f}/S_{s})^{-1.6}$
where
![]() $S$
is the total area of the surface without roughness (Sigal & Danberg Reference Sigal and Danberg1990). The fractal dimension of surface B2 is calculated from the slope of the power density spectrum versus the wavenumber,
$S$
is the total area of the surface without roughness (Sigal & Danberg Reference Sigal and Danberg1990). The fractal dimension of surface B2 is calculated from the slope of the power density spectrum versus the wavenumber,
![]() $C\propto q^{-4.65}$
, for details we refer to Persson et al. (Reference Persson, Albohr, Tartaglino, Volokitin and Tosatti2005). Here we find a Hurst exponent
$C\propto q^{-4.65}$
, for details we refer to Persson et al. (Reference Persson, Albohr, Tartaglino, Volokitin and Tosatti2005). Here we find a Hurst exponent
![]() $H$
of 1.32 and a fractal dimension
$H$
of 1.32 and a fractal dimension
![]() $D$
of 1.68. As such we conclude that the surface can at no scale be considered fractal.
$D$
of 1.68. As such we conclude that the surface can at no scale be considered fractal.