Published online by Cambridge University Press: 22 February 2023
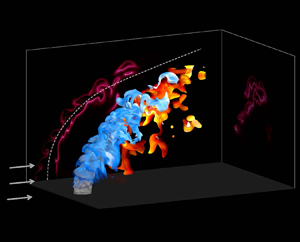
In the present work, direct numerical simulation of a laboratory-scale lean premixed reacting jet in cross-flow was performed to explore the flow–flame structures and turbulence–flame interactions. A jet of lean premixed ethylene–air mixtures (equivalence ratio  $\phi = 0.6$) was injected into a hot vitiated cross-flow. Both non-reacting and reacting cases were simulated. It was found that the reacting jet penetrates deeper in the cross-flow with a weaker shear layer compared with the non-reacting one. The wake of the non-reacting and reacting jet is characterized by vertical vortices and recirculation zones, respectively. As for the flame structure of the reacting case, the reaction intensity varies considerably in different flame zones. The heat release rate on the leeward side is higher than that on the windward side, but lower than that of the corresponding laminar flame. The analysis of the turbulence–flame interactions of the reacting case showed that the large local Damköhler number (
$\phi = 0.6$) was injected into a hot vitiated cross-flow. Both non-reacting and reacting cases were simulated. It was found that the reacting jet penetrates deeper in the cross-flow with a weaker shear layer compared with the non-reacting one. The wake of the non-reacting and reacting jet is characterized by vertical vortices and recirculation zones, respectively. As for the flame structure of the reacting case, the reaction intensity varies considerably in different flame zones. The heat release rate on the leeward side is higher than that on the windward side, but lower than that of the corresponding laminar flame. The analysis of the turbulence–flame interactions of the reacting case showed that the large local Damköhler number ( $Da$) related to reaction-induced dilatations results in an increased tendency of the scalar gradient to align with the most extensive strain rate, which is more evident in the regions with high heat release rate on the leeward side. Negative dilatation regions with positive tangential strain rate and negative normal strain rate are observed on the windward side. High positive dilatations appear on the flame front of the leeward side. The tangential strain rate is negatively correlated with the normal strain rate and curvature. Regions with a high local
$Da$) related to reaction-induced dilatations results in an increased tendency of the scalar gradient to align with the most extensive strain rate, which is more evident in the regions with high heat release rate on the leeward side. Negative dilatation regions with positive tangential strain rate and negative normal strain rate are observed on the windward side. High positive dilatations appear on the flame front of the leeward side. The tangential strain rate is negatively correlated with the normal strain rate and curvature. Regions with a high local  $Da$ on the windward side correspond with high positive curvature regions.
$Da$ on the windward side correspond with high positive curvature regions.