Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-26T23:26:55.871Z Has data issue: false hasContentIssue false
  • English
  • Français

Direct numerical simulation of turbulent channel flow over porous walls

Published online by Cambridge University Press:  04 November 2015

Marco E. Rosti Open the ORCID record for Marco E. Rosti [Opens in a new window] ,
Luca Cortelezzi  and
Maurizio Quadrio
Marco E. Rosti
Affiliation:
Department of Aerospace Science and Technology, Politecnico di Milano, Campus Bovisa, 20136 Milano, Italy
Luca Cortelezzi
Affiliation:
Department of Mechanical Engineering, McGill University, Montreal, Quebec H3A 2K6, Canada
Maurizio Quadrio*
Affiliation:
Department of Aerospace Science and Technology, Politecnico di Milano, Campus Bovisa, 20136 Milano, Italy
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We perform direct numerical simulations (DNS) of a turbulent channel flow over porous walls. In the fluid region the flow is governed by the incompressible Navier–Stokes (NS) equations, while in the porous layers the volume-averaged Navier–Stokes (VANS) equations are used, which are obtained by volume-averaging the microscopic flow field over a small volume that is larger than the typical dimensions of the pores. In this way the porous medium has a continuum description, and can be specified without the need of a detailed knowledge of the pore microstructure by independently assigning permeability and porosity. At the interface between the porous material and the fluid region, momentum-transfer conditions are applied, in which an available coefficient related to the unknown structure of the interface can be used as an error estimate. To set up the numerical problem, the velocity–vorticity formulation of the coupled NS and VANS equations is derived and implemented in a pseudo-spectral DNS solver. 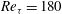Most of the simulations are carried out at $Re_{{\it\tau}}=180$ and consider low-permeability materials; a parameter study is used to describe the role played by permeability, porosity, thickness of the porous material, and the coefficient of the momentum-transfer interface conditions. Among them permeability, even when very small, is shown to play a major role in determining the response of the channel flow to the permeable wall. Turbulence statistics and instantaneous flow fields, in comparative form to the flow over a smooth impermeable wall, are used to understand the main changes introduced by the porous material. A simulation at higher Reynolds number is used to illustrate the main scaling quantities.

JFM classification

Low-Reynolds-number flows: Porous media Turbulent Flows: Turbulent boundary layers
Type
Papers
Information
Journal of Fluid Mechanics , Volume 784 , 10 December 2015 , pp. 396 - 442
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Present address: Aeronautical and Mechanical Engineering, City University London, Northampton Square, London EC1V 0HB, UK.

References

Alazmi, B. & Vafai, K. 2001 Analysis of fluid flow and heat transfer interfacial conditions between a porous medium and a fluid layer. Intl J. Heat Mass Transfer 44 (9), 1735–1749.Google Scholar
Beavers, G. S. & Joseph, D. D. 1967 Boundary conditions at a naturally permeable wall. J. Fluid Mech. 30 (1), 197–207.CrossRefGoogle Scholar
Beavers, G. S., Sparrow, E. M. & Magnuson, R. A. 1970 Experiments on coupled parallel flows in a channel and a bounding porous medium. Trans. ASME J. Basic Engng 92, 843–848.CrossRefGoogle Scholar
Bird, R. B., Stewart, W. E. & Lightfoot, E. N. 2002 Transport Phenomena. John Wiley.Google Scholar
Breugem, W. P. & Boersma, B. J. 2005 Direct numerical simulations of turbulent flow over a permeable wall using a direct and a continuum approach. Phys. Fluids 17, 025103.Google Scholar
Breugem, W. P., Boersma, B. J. & Uittenbogaard, R. E. 2006 The influence of wall permeability on turbulent channel flow. J. Fluid Mech. 562 (1), 35–72.Google Scholar
Chandesris, M., D’Hueppe, A., Mathieu, B., Jamet, D. & Goyeau, B. 2013 Direct numerical simulation of turbulent heat transfer in a fluid-porous domain. Phys. Fluids 25 (12), 125110.Google Scholar
Chandesris, M. & Jamet, D. 2006 Boundary conditions at a planar fluid-porous interface for a Poiseuille flow. Intl J. Heat Mass Transfer 49, 2137–2150.CrossRefGoogle Scholar
Chandesris, M. & Jamet, D. 2007 Boundary conditions at a planar fluid-porous interface: an a priori estimation of the stress jump coefficients. Intl J. Heat Mass Transfer 50 (17–18), 3422–3436.Google Scholar
Chandesris, M. & Jamet, D. 2009 Derivation of jump conditions for the turbulence $k$ -model at a fluid/porous interface. Intl J. Heat Fluid Flow 30 (2), 306–318.CrossRefGoogle Scholar
Finnigan, J. 2000 Turbulence in plant canopies. Annu. Rev. Fluid Mech. 32, 519–571.CrossRefGoogle Scholar
Fukagata, K., Iwamoto, K. & Kasagi, N. 2002 Contribution of Reynolds stress distribution to the skin friction in wall-bounded flows. Phys. Fluids 14 (11), L73–L76.CrossRefGoogle Scholar
Garcia-Mayoral, R. & Jiménez, J. 2011 Drag reduction by riblets. Phil. Trans. R. Soc. Lond. A 369 (1940), 1412–1427.Google ScholarPubMed
Goyeau, B., Lhuillier, D., Gobin, D. & Velarde, M. G. 2003 Momentum transport at a fluid–porous interface. Intl J. Heat Mass Transfer 46 (21), 4071–4081.Google Scholar
Hahn, S., Je, J. & Choi, H. 2002 Direct numerical simulation of turbulent channel flow with permeable wall. J. Fluid Mech. 450, 259–285.CrossRefGoogle Scholar
Hasegawa, Y., Quadrio, M. & Frohnapfel, B. 2014 Numerical simulation of turbulent duct flows at constant power input. J. Fluid Mech. 750, 191–209.Google Scholar
Irmay, S. 1965 Modéles théoriques d’écoulement dans le corps poreaux. Bull. Rilem 29, 37–43.Google Scholar
Jiménez, J., Uhlmann, M., Pinelli, A. & Kawahara, G. 2001 Turbulent shear flow over active and passive porous surfaces. J. Fluid Mech. 442, 89–117.Google Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.Google Scholar
Kong, F. Y. & Schetz, J. A.1982 Turbulent boundary layer over porous surfaces with different surface geometries. AIAA Paper 82-0030.Google Scholar
Laadhari, F. 2007 Reynolds number effect on the dissipation function in wall-bounded flows. Phys. Fluids 19, 038101.CrossRefGoogle Scholar
Lage, J. L. 1998 The fundamental theory of flow through permeable media from Darcy to turbulence. In Transport Phenomena in Porous Media, pp. 1–30. Pergamon.Google Scholar
Liu, Q. & Prosperetti, A. 2011 Pressure-driven flow in a channel with porous walls. J. Fluid Mech. 679, 77–100.Google Scholar
Lovera, F. & Kennedy, J. F. 1969 Friction factors for flat bed flows in sand channels. J. Hydraul. Div. ASCE 95, 1227–1234.Google Scholar
Luchini, P. & Quadrio, M. 2006 A low-cost parallel implementation of direct numerical simulation of wall turbulence. J. Comput. Phys. 211 (2), 551–571.Google Scholar
Macdonald, I. F., El-Sayed, M. S., Mow, K. & Dullien, F. A. L. 1979 Flow through porous media – the Ergun equation revisited. Ind. Engng Chem. Fundam. 18 (3), 199–208.Google Scholar
Minale, M. 2014a Momentum transfer within a porous medium. I. Theoretical derivation of the momentum balance on the solid skeleton. Phys. Fluids 26, 123101.Google Scholar
Minale, M. 2014b Momentum transfer within a porous medium. II. Stress boundary condition. Phys. Fluids 26, 123102.Google Scholar
Neale, G. & Nader, W. 1974 Practical significance of Brinkman’s extension of Darcy’s law: coupled parallel flows within a channel and a bounding porous medium. Can. J. Chem. Engng 52 (4), 475–478.Google Scholar
Ochoa-Tapia, J. A. & Whitaker, S. 1995a Momentum transfer at the boundary between a porous medium and a homogeneous fluid. I: theoretical development. Intl J. Heat Mass Transfer 38 (14), 2635–2646.Google Scholar
Ochoa-Tapia, J. A. & Whitaker, S. 1995b Momentum transfer at the boundary between a porous medium and a homogeneous fluid. II: comparison with experiment. Intl J. Heat Mass Transfer 38 (14), 2647–2655.CrossRefGoogle Scholar
Ochoa-Tapia, J. A. & Whitaker, S. 1998 Momentum jump condition at the boundary between a porous medium and a homogeneous fluid: inertial effects. J. Porous Media 1, 201–218.Google Scholar
Perot, B. & Moin, P. 1995 Shear-free turbulent boundary layers. Part I. Physical insights into near-wall turbulence. J. Fluid Mech. 295, 199–227.Google Scholar
Quadrio, M. 2011 Drag reduction in turbulent boundary layers by in-plane wall motion. Phil. Trans. R. Soc. Lond. A 369 (1940), 1428–1442.Google ScholarPubMed
Quadrio, M., Rosti, M. E., Scarselli, D. & Cortelezzi, D. 2013 On the effects of porous wall on transitional and turbulent channel flows. In Proceedings of European Turbulence Conference ETC14, available at: http://etc14.ens-lyon.fr/etc-14-proceedings/accepted-talks/.Google Scholar
Quintard, M. & Whitaker, S. 1994 Transport in ordered and disordered porous media. II: generalized volume averaging. Transp. Porous Med. 14 (2), 179–206.Google Scholar
Ricco, P., Ottonelli, C., Hasegawa, Y. & Quadrio, M. 2012 Changes in turbulent dissipation in a channel flow with oscillating walls. J. Fluid Mech. 700, 77–104.CrossRefGoogle Scholar
Ruff, J. F. & Gelhar, L. W. 1972 Turbulent shear flow in porous boundary. J. Engng Mech. Div. 98, 975–991.CrossRefGoogle Scholar
Shimizu, Y., Tsujimoto, T. & Nakagawa, H. 1990 Experiment and macroscopic modelling of flow in highly permeable porous medium under free-surface flow. J. Hydrosci. Hydraul. Engng 8, 69–78.Google Scholar
Slattery, J. C. 1967 Flow of viscoelastic fluids through porous media. AIChE J. 13 (6), 1066–1071.CrossRefGoogle Scholar
Sparrow, E. M., Beavers, G. S., Chen, T. S. & Lloyd, J. R. 1973 Breakdown of the laminar flow regime in permeable-walled ducts. Trans. ASME J. Appl. Mech. 40, 337–342.Google Scholar
Suga, K., Matsumura, Y., Ashitaka, Y., Tominaga, S. & Kaneda, M. 2010 Effects of wall permeability on turbulence. Intl J. Heat Fluid Flow 31, 974–984.Google Scholar
Tilton, N. & Cortelezzi, L. 2006 The destabilizing effects of wall permeability in channel flows: A linear stability analysis. Phys. Fluids 18, 051702.CrossRefGoogle Scholar
Tilton, N. & Cortelezzi, L. 2008 Linear stability analysis of pressure-driven flows in channels with porous walls. J. Fluid Mech. 604, 411–446.Google Scholar
Tilton, N. & Cortelezzi, L. 2015 Stability of boundary layers over porous walls with suction. AIAA J. 53 (10), 2856–2868.Google Scholar
Vafai, K. & Kim, S. J. 1990 Fluid mechanics of the interface region between a porous medium and a fluid layer: An exact solution. Intl J. Heat Fluid Flow 11 (3), 254–256.Google Scholar
Vafai, K. & Thiyagaraja, R. 1987 Analysis of flow and heat transfer at the interface region of a porous medium. Intl J. Heat Mass Transfer 30 (7), 1391–1405.Google Scholar
Valdés-Parada, F., Aguilar-Madera, C. G., Ochoa-Tapia, J. A. & Goyeay, B. 2013 Velocity and stress jump conditions between a porous medium and a fluid. Adv. Water Resour. 62, 327–339.CrossRefGoogle Scholar
Valdés-Parada, F. J., Goyeau, B. & Ochoa-Tapia, J. A. 2007 Jump momentum boundary condition at a fluid–porous dividing surface: derivation of the closure problem. Chem. Engng Sci. 62 (15), 4025–4039.Google Scholar
Whitaker, S. 1969 Advances in theory of fluid motion in porous media. Ind. Engng Chem. 61 (12), 14–28.Google Scholar
Whitaker, S. 1986 Flow in porous media. I: a theoretical derivation of Darcy’s law. Transp. Porous Med. 1 (1), 3–25.Google Scholar
Whitaker, S. 1996 The Forchheimer equation: a theoretical development. Transp. Porous Med. 25 (1), 27–61.Google Scholar
Zagni, A. F. E. & Smith, K. V. H. 1976 Channel flow over permeable beds of graded spheres. J. Hydraul. Div. 102, 207–222.CrossRefGoogle Scholar
Zhang, Q. & Prosperetti, A. 2009 Pressure-driven flow in a two-dimensional channel with porous walls. J. Fluid Mech. 631, 1–21.Google Scholar
Zippe, H. J. & Graf, W. H. 1983 Turbulent boundary-layer flow over permeable and non-permeable rough surfaces. J. Hydraul. Res. 21, 51–65.Google Scholar