Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-19T23:53:56.676Z Has data issue: false hasContentIssue false
  • English
  • Français

Direct numerical simulation of turbulence in injection-driven three-dimensional cylindrical flows

Published online by Cambridge University Press:  19 January 2011

JU ZHANG  and
THOMAS L. JACKSON
JU ZHANG*
Affiliation:
Computational Science and Engineering, University of Illinois at Urbana-Champaign, Urbana, IL 61801, USA
THOMAS L. JACKSON
Affiliation:
Computational Science and Engineering, University of Illinois at Urbana-Champaign, Urbana, IL 61801, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Incompressible turbulent flow in a periodic circular pipe with strong injection is studied as a simplified model for the core flow in a solid-propellant rocket motor and other injection-driven internal flows. The model is based on a multi-scale asymptotic approach. The intended application of the current study is erosive burning of solid propellants. Relevant analysis for easily accessible parameters for this application, such as the magnitudes, main frequencies and wavelengths associated with the near-wall shear, and the assessment of near-wall turbulence viscosity is focused on. It is found that, unlike flows with weak or no injection, the near-wall shear is dominated by the root mean square of the streamwise velocity which is a function of the Reynolds number, while the mean streamwise velocity is only weakly dependent on the Reynolds number. As a result, a new wall-friction velocity 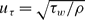, based on the shear stress derived from the sum of the mean and the root mean square, i.e. 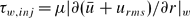, is proposed for the scaling of turbulent viscosity for turbulent flows with strong injection. We also show that the mean streamwise velocity profile has an inflection point near the injecting surface.

JFM classification

Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 670 , 10 March 2011 , pp. 176 - 203
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Apte, S. V. & Yang, V. 2003 A large-eddy simulation study of transition and flow instability in a porous-walled chamber with mass injection. J. Fluid Mech. 477, 215–225.CrossRefGoogle Scholar
Avalon, G., Ugurtas, B., Grisch, F. & Bresson, A. 2000 Numerical computations and visualization tests of the flow inside a cold gas simulation with characterization of a parietal vortex shedding. AIAA Paper 2000-3387.CrossRefGoogle Scholar
Buckmaster, J. & Jackson, T. L. 2000 The effects of time-periodic shear on a diffusion flame anchored to a propellant. Combust. Flame 120, 211–221.CrossRefGoogle Scholar
Cabrit, O. & Nicoud, F. 2009 Direct simulations for wall modeling of multicomponent reacting compressible turbulent flows. Phys. Fluids 21, 055108.CrossRefGoogle Scholar
Culick, F. E. C. 1966 Rotational axisymmetric mean flow and damping of acoustic waves in solid propellant rocket motors. AIAA J. 4, 1462–1464.CrossRefGoogle Scholar
DeGraaff, D. B. & Eaton, J. K. 2000 Reynolds number scaling of the flat-plate turbulent boundary layer. J. Fluid Mech. 422, 319–346.Google Scholar
Deng, Z., Adrian, R. J. & Tomkins, C. D. 2002 Sensitivity of turbulence in transpired channel to injection velocity small-scale non-uniformity. AIAA J. 11, 2241–2246.CrossRefGoogle Scholar
Eggels, J. G. M., Westerweel, J., Nieuwstadt, E. T. M. & Adrian, R. J. 1993 Direct numerical simulation of turbulent pipe flow. Appl. Sci. Res. 51, 319–324.CrossRefGoogle Scholar
Fabignon, Y., Dupays, J., Avalon, G., Vuillot, F., Lupoglazoff, N., Casalis, G. & Prevost, M. 2003 Instabilities and pressure oscillations in solid rocket motors. Aerosp. Sci. Technol. 7, 191–200.CrossRefGoogle Scholar
Green, L. 1954 Erosive burning of some composite solid propellants. Jet Propul. 24, 9–15.CrossRefGoogle Scholar
Hu, F. Q., Hussaini, M. Y. & Manthey, J. L. 1996 Low-dissipation and -dispersion Runge–Kutta schemes for computational acoustics. J. Comput. Phys. 124, 177–191.Google Scholar
Isfahani, A. H. G., Zhang, J. & Jackson, T. L. 2009 The effects of turbulence-induced time-periodic shear on a flame anchored to a propellant. Combust. Flame 156, 1084–1098.Google Scholar
Jiang, G. S. & Shu, C.-W. 1996 Efficient implementation of weighted ENO schemes. J. Comput. Phys. 126, 202.CrossRefGoogle Scholar
Kim, J. & Moin, P. 1985 Application of a fractional-step method to incompressible Navier–Stokes equations. J. Comput. Phys. 59, 308–323.Google Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.Google Scholar
King, M. K. 1993 Erosive burning of solid propellants. J. Propul. Power 9, 785–805.CrossRefGoogle Scholar
Lupoglazoff, N. & Vuillot, F. 1996 Parietal vortex shedding as a cause of instability for long solid propellant motors – numerical simulations and comparisons with firing tests. AIAA Paper 96-0761.CrossRefGoogle Scholar
Lupoglazoff, N. & Vuillot, F. 1998 Numerical simulations of parietal vortex-shedding phenomenon in a cold flow set-up. AIAA Paper 98-3220.CrossRefGoogle Scholar
Moser, R. D., Kim, J. & Mansour, N. N. 1999 Direct numerical simulation of turbulent channel flow up to Re τ = 590. Phys. Fluids 11 (4), 943–945.Google Scholar
Nicoud, F. C. & Angilella, J. R. 1997 Effects of uniform injection at the wall on the stability of Couette-like flows. Phys. Rev. E 56, 3, 3000–3009.Google Scholar
Nicoud, F. C., Poinsot, T. J. & Ha Minh, H. 1995 Direct numerical simulation of turbulent flow with massive uniform injection. In 10th Symposium on Turbulent Shear Flows, Pennsylvania State University, University Park, PA.Google Scholar
Proudman, I. 1960 An example of steady laminar flow at large Reynolds number. J. Fluid Mech. 9, 593–602.CrossRefGoogle Scholar
Spalart, P. 1988 Direct simulation of a turbulent boundary layer up to Re θ = 1410. J. Fluid Mech. 187, 61–98.CrossRefGoogle Scholar
Spalding, D. B. 1961 A single formula for the law of the wall. J. Appl. Mech. 28, 455–457.Google Scholar
Stevenson, T. N. 1963 A law of the wall for turbulent boundary layers with suction or injection. Aero Rep. 166. Cranfield College of Aeronautics.Google Scholar
Sumitani, Y. & Kasagi, N. 1995 Direct numerical simulation of turbulent transport with uniform wall injection and suction. AIAA J. 33, 1220–1228.CrossRefGoogle Scholar
Taylor, G. I. 1956 Fluid flow in regions bounded by porous surfaces. Proc. R. Soc. Lond. A 234, 456–475.Google Scholar
Traineau, J. C., Hervat, P. & Kuentzmann, P. 1986 Cold flow simulation of a two dimensional nozzleless solid rocket motor. AIAA Paper 86-1447.Google Scholar
Venugopal, P., Moser, R. D. & Najjar, F. M. 2008 Direct numerical simulation of turbulence in injection driven plane channel flows. Phys. Fluids 20, 105103.Google Scholar
Wasistho, B. & Moser, R. D. 2005 Simulation strategy of turbulent flow in solid rocket motor. J. Propul. Power 21, 251–263.CrossRefGoogle Scholar
Zhang, J. & Jackson, T. L. 2009 A high-order incompressible flow solver with WENO. J. Comput. Phys. 228, 2426–2442.Google Scholar
Zhang, J. & Jackson, T. L. 2010 A model for erosive burning of homogeneous propellants. Combust. Flame 157 (2), 397–407.Google Scholar