Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-17T07:24:29.443Z Has data issue: false hasContentIssue false
  • English
  • Français

Direct numerical simulation of conical shock wave–turbulent boundary layer interaction

Published online by Cambridge University Press:  19 August 2019

Feng-Yuan Zuo Open the ORCID record for Feng-Yuan Zuo [Opens in a new window] ,
Antonio Memmolo ,
Guo-ping Huang  and
Sergio Pirozzoli Open the ORCID record for Sergio Pirozzoli [Opens in a new window]
Feng-Yuan Zuo*
Affiliation:
College of Energy and Power Engineering, Nanjing University of Aeronautics and Astronautics, 210016 Nanjing, PR China Dipartimento di Meccanica e Aerospaziale, Sapienza Università e di Roma, Via Eudossiana 18, 00184 Roma, Italy
Antonio Memmolo
Affiliation:
Dipartimento di Meccanica e Aerospaziale, Sapienza Università e di Roma, Via Eudossiana 18, 00184 Roma, Italy
Guo-ping Huang
Affiliation:
College of Energy and Power Engineering, Nanjing University of Aeronautics and Astronautics, 210016 Nanjing, PR China
Sergio Pirozzoli*
Affiliation:
Dipartimento di Meccanica e Aerospaziale, Sapienza Università e di Roma, Via Eudossiana 18, 00184 Roma, Italy
*
†Email addresses for correspondence: [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Direct numerical simulation of the Navier–Stokes equations is carried out to investigate the interaction of a conical shock wave with a turbulent boundary layer developing over a flat plate at free-stream Mach number 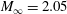$M_{\infty }=2.05$ and Reynolds number 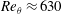$Re_{\unicode[STIX]{x1D703}}\approx 630$, based on the upstream boundary layer momentum thickness. The shock is generated by a circular cone with half opening angle 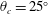$\unicode[STIX]{x1D703}_{c}=25^{\circ }$. As found in experiments, the wall pressure exhibits a distinctive N-wave signature, with a sharp peak right past the precursor shock generated at the cone apex, followed by an extended zone with favourable pressure gradient, and terminated by the trailing shock associated with recompression in the wake of the cone. The boundary layer behaviour is strongly affected by the imposed pressure gradient. Streaks are suppressed in adverse pressure gradient (APG) zones, but re-form rapidly in downstream favourable pressure gradient (FPG) zones. Three-dimensional mean flow separation is only observed in the first APG region associated with the formation of a horseshoe vortex, whereas the second APG region features an incipient detachment state, with scattered spots of instantaneous reversed flow. As found in canonical geometrically two-dimensional wedge-generated shock–boundary layer interactions, different amplification of the turbulent stress components is observed through the interacting shock system, with approach to an isotropic state in APG regions, and to a two-component anisotropic state in FPG. The general adequacy of the Boussinesq hypothesis is found to predict the spatial organization of the turbulent shear stresses, although different eddy viscosities should be used for each component, as in tensor eddy-viscosity models, or in full Reynolds stress closures.

JFM classification

Aerodynamics: High-speed flow Compressible Flows: Compressible boundary layers Compressible Flows: Shock waves
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 877 , 25 October 2019 , pp. 167 - 195
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adams, N. A. 2000 Direct simulation of the turbulent boundary layer along a compression ramp at M = 3 and Re 𝜃 = 1685. J. Fluid Mech. 420, 47–83.10.1017/S0022112000001257Google Scholar
Aubard, G., Gloerfelt, X. & Robinet, J. C. 2013 Large-eddy simulation of broadband unsteadiness in a shock/boundary-layer interaction. AIAA J. 51 (10), 2395–2409.10.2514/1.J052249Google Scholar
Aubertine, C. D. & Eaton, J. K. 2005 Turbulence development in a non-equilibrium turbulent boundary layer with mild adverse pressure gradient. J. Fluid Mech. 532, 345–364.10.1017/S0022112005004143Google Scholar
Babinsky, H. & Harvey, J. K. 2011 Shock Wave-Boundary-Layer Interactions. Cambridge University Press.10.1017/CBO9780511842757Google Scholar
Bernardini, M., Modesti, D. & Pirozzoli, S. 2016 On the suitability of the immersed boundary method for the simulation of high-Reynolds-number separated turbulent flows. Comput. Fluids 130, 84–93.10.1016/j.compfluid.2016.02.018Google Scholar
Castillo, L. & George, W. K. 2001 Similarity analysis for turbulent boundary layer with pressure gradient: outer flow. AIAA J. 39 (1), 41–47.10.2514/2.1300Google Scholar
Chong, M. S., Perry, A. E. & Cantwell, B. J. 1990 A general classification of three-dimensional flow fields. Phys. Fluids A 2 (5), 765–777.10.1063/1.857730Google Scholar
Clauser, F. H. 1954 Turbulent boundary layers in adverse pressure gradients. J. Aero. Sci. 21 (2), 91–108.Google Scholar
Dallmann, U. 1983 Topological structures of three-dimensional vortex flow separation. In 16th Fluid and Plasmadynamics Conference, p. 1735. American Institute of Aeronautics and Astronautics.Google Scholar
DeBonis, J. R., Oberkampf, W. L., Wolf, R. T., Orkwis, P. D., Turner, M. G., Babinsky, H. & Benek, J. A. 2012 Assessment of computational fluid dynamics and experimental data for shock boundary-layer interactions. AIAA J. 50 (4), 891–903.10.2514/1.J051341Google Scholar
Délery, J. M. 2001 Robert Legendre and Henry Werlé: toward the elucidation of three-dimensional separation. Annu. Rev. Fluid Mech. 33, 129–154.10.1146/annurev.fluid.33.1.129Google Scholar
Délery, J. M. & Dussauge, J. P. 2009 Some physical aspects of shock wave/boundary layer interactions. Shock Waves 19 (6), 453–468.10.1007/s00193-009-0220-zGoogle Scholar
Dolling, D. S. 2001 Fifty years of shock-wave/boundary-layer interaction research: what next? AIAA J. 39 (8), 1517–1531.10.2514/2.1476Google Scholar
Dupont, P., Haddad, C. & Debieve, J. F. 2006 Space and time organization in a shock-induced separated boundary layer. J. Fluid Mech. 559, 255–277.10.1017/S0022112006000267Google Scholar
Emory, M., Pecnik, R. & Iaccarino, G. 2011 Modeling structural uncertainties in Reynolds-averaged computations of shock/boundary layer interactions. In 49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition 2011-479, American Institute of Aeronautics and Astronautics.Google Scholar
Fadlun, E. A., Verzicco, R., Orlandi, P. & Mohd-Yusof, J. 2000 Combined immersed-boundary finite-difference methods for three-dimensional complex flow simulations. J. Comput. Phys. 161 (1), 35–60.10.1006/jcph.2000.6484Google Scholar
Gai, S. L. & Teh, S. L. 2000 Interaction between a conical shock wave and a plane turbulent boundary layer. AIAA J. 38 (5), 804–811.10.2514/2.1060Google Scholar
Gerolymos, G. A., Sauret, E. & Vallet, I. 2004 Oblique-shock-wave/boundary-layer interaction using near-wall Reynolds-stress models. AIAA J. 42, 1089–1100.10.2514/1.1984Google Scholar
Hadjadj, A. 2012 Large-Eddy Simulation of Shock/Boundary-Layer Interaction. AIAA J. 50 (12), 2919–2927.10.2514/1.J051786Google Scholar
Hale, J.2015 Interaction between a conical shock wave and a plane compressible turbulent boundary layer at Mach 2.05. PhD thesis, UIUC.Google Scholar
Herrin, J. L. & Dutton, J. C. 1994 Supersonic base flow experiments in the near wake of a cylindrical afterbody. AIAA J. 32 (1), 77–83.10.2514/3.11953Google Scholar
Kiya, M. & Sasaki, K. 1983 Structure of a turbulent separation bubble. J. Fluid Mech. 137, 83–113.10.1017/S002211208300230XGoogle Scholar
Knight, D. D., Horstman, C., Bogdonoff, S. & Shapey, B. 1987 Structure of supersonic turbulent flow past a sharp fin. AIAA J. 25 (10), 1331–1337.10.2514/3.9787Google Scholar
Lumley, J. L. 1978 Computational modeling of turbulent flows. Adv. Appl. Mech. 18, 123–176.10.1016/S0065-2156(08)70266-7Google Scholar
Migotsky, E. & Morkovin, M. V. 1951 Three-Dimensional Shock-Wave Reflections. J. Aero. Sci. 18 (7), 484–489.Google Scholar
Morgan, B., Duraisamy, K., Nguyen, N., Kawai, S. & Lele, S. K. 2013 Flow physics and RANS modelling of oblique shock/turbulent boundary layer interaction. J. Fluid Mech. 729, 231–284.10.1017/jfm.2013.301Google Scholar
O’Rourke, J. 1998 Computational geometry in C. Cambridge University Press.10.1017/CBO9780511804120Google Scholar
Panov, Y. A. 1968 Interaction of incident three-dimensional shock with a turbulent boundary layer. Fluid Dyn. 3 (3), 108–110.Google Scholar
Pirozzoli, S. 2010 Generalized conservative approximations of split convective derivative operators. J. Comput. Phys. 229 (19), 7180–7190.10.1016/j.jcp.2010.06.006Google Scholar
Pirozzoli, S. 2011 Numerical methods for high-speed flows. Annu. Rev. Fluid Mech. 43, 163–194.10.1146/annurev-fluid-122109-160718Google Scholar
Pirozzoli, S. & Bernardini, M. 2011a Direct numerical simulation database for impinging shock wave/turbulent boundary-layer interaction. AIAA J. 49 (6), 1307–1312.10.2514/1.J050901Google Scholar
Pirozzoli, S. & Bernardini, M. 2011b Turbulence in supersonic boundary layers at moderate Reynolds number. J. Fluid Mech. 688, 120–168.10.1017/jfm.2011.368Google Scholar
Pirozzoli, S., Bernardini, M. & Grasso, F. 2010 Direct numerical simulation of transonic shock/boundary layer interaction under conditions of incipient separation. J. Fluid Mech. 657, 361–393.10.1017/S0022112010001710Google Scholar
Pirozzoli, S. & Grasso, F. 2006 Direct numerical simulation of impinging shock wave/turbulent boundary layer interaction at M = 2. 25. Phys. Fluids 18 (6), 065113.10.1063/1.2216989Google Scholar
Poinsot, T. J. & Lele, S. K. 1992 Boundary conditions for direct simulations of compressible viscous flows. J. Comput. Phys. 101 (1), 104–129.10.1016/0021-9991(92)90046-2Google Scholar
Simpson, R. L. 1989 Turbulent boundary-layer separation. Annu. Rev. Fluid Mech. 21 (1), 205–232.10.1146/annurev.fl.21.010189.001225Google Scholar
Smits, A. J. & Dussauge, J. P. 2006 Turbulent Shear Layers in Supersonic Flow. Springer Science & Business Media.Google Scholar
Song, S. & Eaton, J. K. 2004 Reynolds number effects on a turbulent boundary layer with separation, reattachment, and recovery. Exp. Fluids 36 (2), 246–258.10.1007/s00348-003-0696-8Google Scholar
Spalart, P. & Allmaras, S. 1992 A one-equation turbulence model for aerodynamic flows. In 30th Aerospace Sciences Meeting and Exhibit, Aerospace Sciences Meetings. American Institute of Aeronautics and Astronautics.Google Scholar
Speziale, C. G. 1987 On nonlinear k-l and k-𝜖 models of turbulence. J. Fluid Mech. 178, 459–475.10.1017/S0022112087001319Google Scholar
Sziroczak, D. & Smith, H. 2016 A review of design issues specific to hypersonic flight vehicles. Prog. Aerosp. Sci. 84, 1–28.10.1016/j.paerosci.2016.04.001Google Scholar
Tessicini, F., Iaccarino, G., Fatica, M., Wang, M. & Verzicco, R. 2002 Wall modeling for large-eddy simulation using an immersed boundary method. CTR Annu. Res. Briefs, Stanford, CA pp. 181–187.Google Scholar
Touber, E. & Sandham, N. D. 2011 Low-order stochastic modelling of low-frequency motions in reflected shock-wave/boundary-layer interactions. J. Fluid Mech. 671, 417–465.10.1017/S0022112010005811Google Scholar
Wu, X. & Moin, P. 2009 Direct numerical simulation of turbulence in a nominally zero-pressure-gradient flat-plate boundary layer. J. Fluid Mech. 630, 5–41.10.1017/S0022112009006624Google Scholar
Xu, S. & Martin, M. P. 2004 Assessment of inflow boundary conditions for compressible turbulent boundary layers. Phys. Fluids 16 (7), 2623–2639.10.1063/1.1758218Google Scholar
Zagarola, M. V. & Smits, A. J. 1998 Mean-flow scaling of turbulent pipe flow. J. Fluid Mech. 373, 33–79.10.1017/S0022112098002419Google Scholar
Zhou, J., Adrian, R. J., Balachandar, S. & Kendall, T. M. 1999 Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 387, 353–396.10.1017/S002211209900467XGoogle Scholar
Zuo, F. & Huang, G. 2018 Numerical investigation of bleeding control method on section-controllable wavecatcher intakes. Acta Astron. 151, 572–584.10.1016/j.actaastro.2018.06.059Google Scholar
Zuo, F., Huang, G. & Xia, C. 2016 Investigation of internal-waverider-inlet flow pattern integrated with variable-geometry for TBCC. Aerosp. Sci. Technol. 59, 69–77.10.1016/j.ast.2016.10.009Google Scholar

Zuo et al. supplementary movie 1

Overall structure of the CSBLI. The cone geometry is blanked, and shock waves are shown by means of numerical schlieren, defined through the magnitude of the density gradient ( ). Contours range , from black to white.

Download Zuo et al. supplementary movie 1(Video)
Video 9.9 MB

Zuo et al. supplementary movie 2

Three-dimensional view of CSBLI. The shock structure is educed through the pressure iso-surface . Streamwise velocity contours are shown for (color scale from blue to red) in a near-wall plane at y+=10.5. Pressure contours are shown in a side plane for (color scale from blue to red).

Download Zuo et al. supplementary movie 2(Video)
Video 9.8 MB

Zuo et al. supplementary movie 3

Vortical structures in CSBLI. Vortices are educed through the iso-surface of the swirling strength ( ), and colored with the wall-normal velocity ( , color scale from blue to red).

Download Zuo et al. supplementary movie 3(Video)
Video 9.6 MB