Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-25T14:48:20.776Z Has data issue: false hasContentIssue false
  • English
  • Français

Direct numerical simulation of a spatially developing compressible plane mixing layer: flow structures and mean flow properties

Published online by Cambridge University Press:  28 September 2012

Qiang Zhou ,
Feng He  and
M. Y. Shen
Qiang Zhou
Affiliation:
Department of Engineering Mechanics, School of Aerospace, Tsinghua University, Beijing 100084, PR China
Feng He*
Affiliation:
Department of Engineering Mechanics, School of Aerospace, Tsinghua University, Beijing 100084, PR China
M. Y. Shen
Affiliation:
Department of Engineering Mechanics, School of Aerospace, Tsinghua University, Beijing 100084, PR China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The spatially developing compressible plane mixing layer with a convective Mach number of 0.7 is investigated by direct numerical simulation. A pair of equal and opposite oblique instability waves is introduced to perturb the mixing layer at the inlet. The full evolution process of instability, including formation of 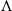-vortices and hairpin vortices, breakdown of large structures and establishment of self-similar turbulence, is presented clearly in the simulation. In the transition process, the flow fields are populated sequentially by 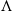-vortices, hairpin vortices and ‘flower’ structures. This is the first direct evidence showing the dominance of these structures in the spatially developing mixing layer. Hairpin vortices are found to play an important role in the breakdown of the flow. The legs of hairpin vortices first evolve into sheaths with intense vorticity then break up into small slender vortices. The later flower structures are produced by the instability of the heads of the hairpin vortices. They prevail for a long distance in the mixing layer until the flow starts to settle down into its self-similar state. The preponderance of slender inclined streamwise vortices is observed in the transversal middle zone of the transition region after the breakup of the hairpin legs. This predominance of streamwise vortices also persists in the self-similar turbulent region, though the vortices there are found to be relatively very weak. The evolution of both the mean streamwise velocity profile and the Reynolds stresses is found to have close connection to the behaviour of the large vortex structures. High growth rates of the momentum and vorticity thicknesses are observed in the transition region of the flow. The growth rates in the self-similar turbulence region decay to a value that agrees well with previous experimental and numerical studies. Shocklets occur in the simulation, and their formation mechanisms are elaborated and categorized. This is the first three-dimensional simulation that captures shocklets at this low convective Mach number.

JFM classification

Turbulent Flows: Compressible turbulence Boundary Layers: Free shear layers Instability: Transition to turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 711 , 25 November 2012 , pp. 437 - 468
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Barre, S., Braud, P., Chambres, O. & Bonnet, J. P. 1997 Influence of inlet pressure conditions on supersonic turbulent mixing layers. Exp. Therm. Fluid Sci. 14 (1), 68–74.CrossRefGoogle Scholar
2. Batchelor, G. K. 1959 The Theory of Homogeneous Turbulence. Cambridge University Press.Google Scholar
3. Birch, S. F. & Eggers, J. M. 1973 Free turbulent shear flows. Tech. Rep. SP-321. NASA.Google Scholar
4. Bogdanoff, D. W. 1983 Compressibility effects in turbulent shear layers. AIAA J. 21, 926–927.CrossRefGoogle Scholar
5. Brown, G. L. & Roshko, A. 1974 On density effects and large structure in turbulent mixing layers. J. Fluid Mech. 64, 775–816.CrossRefGoogle Scholar
6. Clemens, N. T. & Mungal, M. G. 1992 Two- and three-dimensional effects in the supersonic mixing layer. AIAA J. 30, 973–981.CrossRefGoogle Scholar
7. Clemens, N. T. & Mungal, M. G. 1995 Large-scale structure and entrainment in the supersonic mixing layer. J. Fluid Mech. 284, 171–216.CrossRefGoogle Scholar
8. Davoudzadeh, F., McDonald, H. & Thompson, B. E. 1995 Accuracy evaluation of unsteady cfd numerical schemes by vortex preservation. Comput. Fluids 24, 883–895.CrossRefGoogle Scholar
9. Day, M. J. & Reynolds, W. C. 1998 The structure of the compressible reacting mixing layer: insights from linear stability analysis. Phys. Fluids 10 (4), 993–1007.CrossRefGoogle Scholar
10. Dimotakis, P. E. 1991 Turbulent free shear layer mixing and combustion. In High-speed Flight Propulsion Systems (ed. Murthy, S. N. B. & Curran, E. T. ), Progress in Astronautics and Aeronautics , vol. 137, pp. 265–340. AIAA.Google Scholar
11. Elliott, G. S. & Samimy, M. 1990 Compressibility effects in free shear layers. Phys. Fluids A 2, 1231–1240.CrossRefGoogle Scholar
12. Foss, J. K. & Zaman, K. B. M. Q. 1999 Large- and small- scale vortical motions in a shear layer perturbed by tabs. J. Fluid Mech. 382, 307–329.CrossRefGoogle Scholar
13. Freund, J. B., Lele, S. K. & Moin, P. 2000 Compressibility effects in a turbulent annular mixing layer. Part 1. Turbulence and growth rate. J. Fluid Mech. 421, 229–267.CrossRefGoogle Scholar
14. Fu, D. X., Ma, Y. W. & Zhang, L. B. 2000 Direct numerical simulation of transition and turbulence in compressible mixing layer. Sci. China A 43 (4), 421–429.CrossRefGoogle Scholar
15. Fu, S. & Li, Q. B. 2006 Numerical simulation of compressible mixing layers. Intl J. Heat Fluid Flow 27, 895–901.CrossRefGoogle Scholar
16. Goebel, S. G. & Dutton, J. C. 1991 Experimental study of compressible turbulent mixing layers. AIAA J. 31, 538–546.CrossRefGoogle Scholar
17. Gruber, M. R., Messersmith, N. L. & Dutton, J. C. 1993 Three-dimensional velocity field in a compressible mixing layer. AIAA J. 31, 2061–2067.CrossRefGoogle Scholar
18. Hall, J. L., Dimotakis, P. E. & Rosemann, H. 1993 Experiments in non-reacting compressible shear layers. AIAA J. 31, 2247–2254.CrossRefGoogle Scholar
19. Heisenberg, W. 1948 Zur statistischen theorie der turbulenz. Z. Phys. 124, 628–657.CrossRefGoogle Scholar
20. Jiang, G. S. & Shu, C. W. 1996 Efficient implementation of weighted eno schemes. J. Comput. Phys. 126, 202–228.CrossRefGoogle Scholar
21. Kida, S. & Orszag, S. A. 1990 Enstrophy budget in decaying compressible turbulence. J. Sci. Comput. 5 (1), 1–34.CrossRefGoogle Scholar
22. Kourta, A. & Sauvage, R. 2002 Computation of supersonic mixing layers. Phys. Fluids 14 (11), 3790–3797.CrossRefGoogle Scholar
23. Lele, S. 1989 Direct numerical simulation of compressible free shear flows. AIAA Paper 1989-0374.CrossRefGoogle Scholar
24. Liepmann, H. W. & Laufer, J. 1947 Investigation of free turbulent mixing. Tech. Rep. 1257. NACA.Google Scholar
25. Liou, T., Lien, W. & Hwang, P. 1995 Compressibility effects and mixing enhancement in turbulent free shear flows. AIAA J. 33, 2332–2338.CrossRefGoogle Scholar
26. Moore, C. J. 1978 The effect of shear layer instability on jet exhaust noise. In Structure and Mechanisms of Turbulence (ed. Fiedler, H. ), Lecture Notes in Physics , vol. 76, pp. 254–264. Springer.CrossRefGoogle Scholar
27. Morduchow, M. & Libby, P. A. 1949 On a complete solution of the one-dimensional flow equations of a viscous, heat conducting, compressible gas. J. Aero. Sci. 16, 674–684.Google Scholar
28. Moser, R. D. & Rogers, M. M. 1993 The three-dimensional evolution of a plane mixing layer: pairing and transition to turbulence. J. Fluid Mech. 247, 275–320.CrossRefGoogle Scholar
29. Nygaard, K. J. & Glezer, A. 1991 Evolution of streamwise vortices and generation of small-scale motion in a plane mixing layer. J. Fluid Mech. 231, 257–301.CrossRefGoogle Scholar
30. Olsen, M. G. & Dutton, J. C. 2003 Planar velocity measurements in a weakly compressible mixing layer. J. Fluid Mech. 486, 51–77.CrossRefGoogle Scholar
31. Ortwerth, P. J. & Shine, A. 1977 On the scaling of plane turbulent shear layers. Tech. Rep. TR-77-118. AFWL.Google Scholar
32. Oster, D. & Wygnanski, I. 1982 The forced mixing layer between parallel streams. J. Fluid Mech. 113, 91–130.CrossRefGoogle Scholar
33. Pantano, C. & Sarkar, S. 2002 A study of compressibility effects in the high-speed turbulent shear layer using direct simulation. J. Fluid Mech. 451, 329–371.CrossRefGoogle Scholar
34. Papamoschou, D. 1989 Structure of the compressible turbulent shear layer. AIAA Paper 1989-0126.CrossRefGoogle Scholar
35. Papamoschou, D. 1995 Evidence of shocklets in a counterflow supersonic shear layer. Phys. Fluids 7, 233–235.CrossRefGoogle Scholar
36. Papamoschou, D. & Roshko, A. 1988 The compressible turbulent shear layer: an experimental study. J. Fluid Mech. 197, 453–477.CrossRefGoogle Scholar
37. Pradeep, D. S. & Hussain, F. 2000 Core dynamics of a coherent structures: a prototypical physical-space cascade mechanism? In Turbulence Structure and Vortex Dynamics (ed. Hunt, J. C. R. & Vassilicos, J. C. ). Cambridge University Press.Google Scholar
38. Rogers, M. M. & Moser, R. D. 1992 The three-dimensional evolution of a plane mixing layer: the Kelvin–Helmholtz rollup. J. Fluid Mech. 243, 183–226.CrossRefGoogle Scholar
39. Rossmann, T., Mungal, M. G. & Hanson, R. K. 2002 Evolution and growth of large-scale structures in high compressibility mixing layers. J. Turbul. 3, 009.CrossRefGoogle Scholar
40. Samimy, M. & Elliot, G. S. 1990 Effects of compressibility on the characteristics of free shear layers. AIAA J. 28, 439–445.CrossRefGoogle Scholar
41. Sandham, N. D. & Reynolds, W. C. 1990 Compressible mixing layer: linear theory and direct simulation. AIAA J. 28, 618–624.CrossRefGoogle Scholar
42. Sandham, N. D. & Reynolds, W. C. 1991 Three-dimensional simulations of large eddies in the compressible mixing layer. J. Fluid Mech. 224, 133–158.CrossRefGoogle Scholar
43. Schoppa, W., Hussain, F. & Metcalfe, R. W. 1995 A new mechanism of small-scale transition in a plane mixing layer: core dynamics of spanwise vortices. J. Fluid Mech. 298, 23–80.CrossRefGoogle Scholar
44. Spiteri, R. J. & Ruuth, S. J. 2003 Non-linear evolution using optimal fourth-order strong-stability-preserving Runge–Kutta methods. Math. Comput. Simul. 62, 125–135.CrossRefGoogle Scholar
45. Steger, J. L. & Warming, R. F. 1981 Flux vector splitting of the inviscid gasdynamic equations with application to finite difference methods. J. Comput. Phys. 40, 263–293.CrossRefGoogle Scholar
46. Thompson, K. W. 1987 Time dependent boundary conditions for hyperbolic systems. J. Comput. Phys. 68, 1–24.CrossRefGoogle Scholar
47. Townsend, A. A. 1976 The Structure of Turbulent Shear Flows, 2nd edn. Cambridge University Press.Google Scholar
48. Urban, W. D. & Mungal, M. G. 2001 Planar velocity measurements in compressible mixing layers. J. Fluid Mech. 431, 189–222.CrossRefGoogle Scholar
49. Vreman, B., Kuerten, H. & Geurts, B. 1995 Shocks in direct numerical simulation of the confined three-dimensional mixing layer. Phys. Fluids 7 (9), 2105–2107.CrossRefGoogle Scholar
50. Watanabe, S. & Mungal, M. G. 2005 Velocity fields in mixing-enhanced compressible shear layers. J. Fluid Mech. 522, 141–177.CrossRefGoogle Scholar
51. Wu, X. & Moin, P. 2009 Direct numerical simulation of turbulence in a nominally zero-pressure-gradient flat-plate boundary layer. J. Fluid Mech. 630, 5–41.CrossRefGoogle Scholar
52. Wygnanski, I., Oster, D. & Fiedler, H. 1979 A forced, plane, turbulent mixing-layer: a challenge for the predictor. In Turbulent Shear Flows (ed. Bradbury, L. J. S., Durst, F., Launder, B. E., Schmidt, F. W. & Whitelaw, J. H. ). Springer.Google Scholar
53. Zhou, J., Adrian, R. J. & Balachandar, S. 1999 Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 387, 353–396.CrossRefGoogle Scholar
54. Zhou, Q., Yao, Z. H., He, F. & Shen, M. Y. 2007 A new family of high-order compact upwind difference schemes with good spectral resolution. J. Comput. Phys. 227 (2), 1306–1339.CrossRefGoogle Scholar