Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-23T11:46:32.293Z Has data issue: false hasContentIssue false
  • English
  • Français

Direct numerical simulation of a non-equilibrium three-dimensional turbulent boundary layer over a flat plate

Published online by Cambridge University Press:  09 September 2020

Hiroyuki Abe Open the ORCID record for Hiroyuki Abe [Opens in a new window]
Hiroyuki Abe*
Affiliation:
Japan Aerospace Exploration Agency, Tokyo182-8522, Japan
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

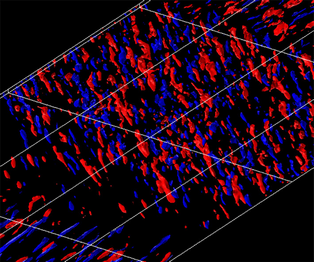
Direct numerical simulations (DNS) are used to examine a spatially developing non-equilibrium three-dimensional turbulent boundary layer (3DTBL) over a flat plate. The present flow is a ‘shear-driven’ 3DTBL owing to a sudden imposition of a surface spanwise velocity ${W_S}$. Particular attention is given to the effects of cross-flow and Reynolds number. In the DNS, three values of the inlet momentum thickness Reynolds number, $R{e_{{\theta _0}}} = 300$, 600 and 900, are used with several values of ${W_S}$. The present largest ${W_S}$ is twice the free-stream velocity ${U_0}$, comparable to the maximum value of the spinning cylinder experiment by Lohmann (Trans. ASME I: J. Fluids Engng, vol. 98, 1976, pp. 354–363). After imposing ${W_S}$, the mean streamwise vorticity ${\overline \varOmega _x}$ increasingly propagates away from the wall where there is close relationship between a deficit of mean streamwise velocity and inviscid skewing (i.e. three-dimensionality). At a downstream station of a 3DTBL, near-plateaus appear in the skin friction coefficients where the magnitudes depend intrinsically on ${W_S}$. The approach to the collateral state is, however, slow for mean streamwise velocity $\overline U$ where the Reynolds shear stress $\overline {uv}$ extracts energy from the mean flow inefficiently. As the Reynolds number increases, the mean velocity magnitude ${Q_r}$ tends to show the log law but with a larger von Kármán constant than in a two-dimensional turbulent boundary layer. Instantaneously, toppling u structures dominate owing to cross-flow and become more prominent with increasing Re. Statistically, the latter spanwise length scale increases linearly with respect to y below y/δ99 = 0.2, which indicates that cross-flow yields a self-similar behaviour.

JFM classification

Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulent boundary layers
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 902 , 10 November 2020 , A20
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abe, H. 2017 Reynolds-number dependence of wall-pressure fluctuations in a pressure-induced turbulent separation bubble. J. Fluid Mech. 833, 563–598.CrossRefGoogle Scholar
Abe, H. 2018 Direct numerical simulation of a shear driven three-dimensional turbulent boundary layer. In Bulletin of the American Physical Society 71st Annual Meeting of the APS Division of Fluid Dynamics, Atlanta, GA, November 18–20, vol. 63 (13), p. 281.Google Scholar
Abe, H. 2019 Direct numerical simulation of a turbulent boundary layer with separation and reattachment over a range of Reynolds numbers. Fluid Dyn. Res. 51, 011409.CrossRefGoogle Scholar
Abe, H. & Antonia, R. A. 2016 Relationship between the energy dissipation function and the skin friction law in a turbulent channel flow. J. Fluid Mech. 798, 140–164.CrossRefGoogle Scholar
Abe, H. & Antonia, R. A. 2017 Relationship between the heat transfer law and the scalar dissipation function in a turbulent channel flow. J. Fluid Mech. 830, 300–325.CrossRefGoogle Scholar
Abe, H., Antonia, R. A. & Toh, S. 2018 Large-scale structures in a turbulent channel flow with a minimal streamwise flow unit. J. Fluid Mech. 850, 733–768.CrossRefGoogle Scholar
Abe, H., Kawamura, H. & Choi, H. 2004 Very large-scale structures and their effects on the wall shear-stress fluctuations in a turbulent channel flow up to $R{e_\tau } = 640$. Trans. ASME J. Fluids Engng 126, 835–843.CrossRefGoogle Scholar
Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.CrossRefGoogle Scholar
Ahn, J., Lee, J. H., Lee, J. L., Kang, J.-H. & Sung, H. J. 2015 Direct numerical simulation of a 30R long turbulent pipe flow at $R{e_\tau } = 3008$. Phys. Fluids 27, 065110.CrossRefGoogle Scholar
Anderson, S. D. & Eaton, J. K. 1989 Reynolds stress development in pressure-driven, three-dimensional, turbulent boundary layers. J Fluid Mech. 202, 263–294.CrossRefGoogle Scholar
Antonia, R. A. & Luxton, R. E. 1971 The response of a turbulent boundary layer to an upstanding step change in surface roughness. Trans. ASME: J. Basic Engng 93, 22–34.CrossRefGoogle Scholar
Antonia, R. A. & Luxton, R. E. 1972 The response of a turbulent boundary layer to a step change in surface roughness. Part 2. Rough-to-smooth. J. Fluid Mech. 53, 737–757.CrossRefGoogle Scholar
Balakumar, B. J. & Adrian, R. J. 2007 Large- and very-large-scale motions in channel and boundary-layer flows. Phil. Trans. R. Soc. A 365, 665–681.CrossRefGoogle ScholarPubMed
Bassina, I., Strelets, M. & Spalart, P. R. 2001 Response of simple turbulence models to step changes of slip velocity. AIAA J. 39, 201–210.CrossRefGoogle Scholar
van den Berg, B., Elsenaar, A., Lindhout, J. P. F. & Wesseling, P. 1975 Measurements in an incompressible three-dimensional turbulent boundary layer, under infinite swept-wing conditions, and comparison with theory. J. Fluid Mech. 70, 127–148.CrossRefGoogle Scholar
Bissonnette, L. R. & Mellor, G. L. 1974 Experiments on the behaviour of an axisymmetric turbulent boundary layer with a sudden circumferential strain. J. Fluid Mech. 63, 369–413.CrossRefGoogle Scholar
Bradshaw, P. 1987 Turbulent secondary flows. Annu. Rev. Fluid Mech. 19, 53–74.CrossRefGoogle Scholar
Bradshaw, P. & Pontikos, N. S. 1985 Measurements in the turbulent boundary layer on an ‘infinite’ swept wing. J. Fluid Mech. 159, 105–130.CrossRefGoogle Scholar
Coleman, G. N., Kim, J. & Le, A.-T. 1996 A numerical study of three-dimensional wall-bounded flows. Intl J. Heat Fluid Flow 17, 333–342.CrossRefGoogle Scholar
Coleman, G. N., Kim, J. & Spalart, P. R. 2000 A numerical study of strained three-dimensional wall-bounded turbulence. J. Fluid Mech. 416, 75–116.CrossRefGoogle Scholar
Coleman, G. N., Rumsey, C. L. & Spalart, P. R. 2019 Numerical study of a turbulent separation bubble with sweep. J. Fluid Mech. 880, 684–706.CrossRefGoogle Scholar
Deck, S., Renard, N., Laraufie, R. & Weiss, P.-E. 2014 Large-scale contribution to mean wall shear stress in high-Reynolds-number flat-plate boundary layers up to $R{e_\theta } = 13650$. J. Fluid Mech. 743, 202–248.CrossRefGoogle Scholar
Driver, D. M. & Hebbar, S. K. 1987 Experimental study of a three-dimensional, shear-driven, turbulent boundary layer. AIAA J. 25, 35–42.CrossRefGoogle Scholar
Driver, D. M. & Johnston, J. P. 1990 Experimental study of a three-dimensional shear-driven turbulent boundary layer with streamwise adverse pressure gradient. NASA TM 102211.Google Scholar
Eaton, J. K. 1995 Effects of mean flow three dimensionality on turbulent boundary-layer structure. AIAA J. 33, 2020–2025.CrossRefGoogle Scholar
Fukagata, K., Iwamoto, K. & Kasagi, N. 2002 Contribution of Reynolds stress distribution to the skin friction in wall-bounded flows. Phys. Fluids 14 (11), 73–76.CrossRefGoogle Scholar
Furuya, Y., Nakamura, I. & Kawachi, H. 1966 The experiment on the skewed boundary layer on a rotating body. Bull. JSME 9 (36), 702–710.CrossRefGoogle Scholar
Guala, M., Hommema, S. E. & Adrian, R. J. 2006 Large-scale and very-large-scale motions in turbulent pipe flow. J. Fluid Mech. 554, 521–542.CrossRefGoogle Scholar
Gungor, A. G., Maciel, Y., Simens, M. & Soria, J. 2014 Analysis of a turbulent boundary layer subjected to a strong adverse pressure gradient. J. Phys.: Conf. Ser. 506, 012007.Google Scholar
Hoyas, S. & Jiménez, J. 2008 Reynolds number effects on the Reynolds-stress budgets in turbulent channels. Phys. Fluids 20, 101511.CrossRefGoogle Scholar
Hutchins, N. & Marusic, I. 2007 Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 467–477.CrossRefGoogle Scholar
Hwang, Y. 2015 Statistical structure of self-sustaining attached eddies in turbulent channel flow. J. Fluid Mech. 767, 254–289.CrossRefGoogle Scholar
Jiménez, J. & Hoyas, S. 2008 Turbulent fluctuations above the buffer layer of wall-bounded flows. J. Fluid Mech. 611, 215–236.CrossRefGoogle Scholar
Johnston, J. P. 1960 On the three-dimensional turbulent boundary layer generated by secondary flow. Trans. ASME: J. Basic Engng 82, 233–246.CrossRefGoogle Scholar
Johnston, J. P. & Flack, K. A. 1996 Review – advances in three-dimensional turbulent boundary layers with emphasis on the wall-layer regions. Trans. ASME: J. Fluids Engng 118, 219–232.Google Scholar
Kang, H. S., Choi, H. & Yoo, J. Y. 1998 On the modification of the near-wall coherent structure in a three-dimensional turbulent boundary layer on a free rotating disk. Phys. Fluids 10, 2315–2322.CrossRefGoogle Scholar
Kannepalli, C. & Piomelli, U. 2000 Large-eddy simulation of a three-dimensional shear-driven turbulent boundary layer. J. Fluid Mech. 423, 175–203.CrossRefGoogle Scholar
Kevin, K., Monty, J. & Hutchins, N. 2019 Turbulent structures in a statistically three-dimensional boundary layer. J. Fluid Mech. 859, 543–565.CrossRefGoogle Scholar
Kiesow, R. O. & Plesniak, M. W. 2003 Near-wall physics of a shear-driven three-dimensional turbulent boundary layer with varying crossflow. J. Fluid Mech. 484, 1–39.CrossRefGoogle Scholar
Kong, H., Choi, H. & Lee, J. S. 2000 Direct numerical simulation of turbulent thermal boundary layers. Phys. Fluids 12, 2555–2568.CrossRefGoogle Scholar
Littell, H. & Eaton, J. 1994 Turbulence characteristics of the boundary layer on a rotating disk. J. Fluid Mech. 266, 175–207.CrossRefGoogle Scholar
Lohmann, R. P. 1976 Response of a developed turbulent boundary layer to local transverse surface motion. Trans. ASME: J. Fluids Engng 98, 354–363.Google Scholar
Lozano-Durán, A., Giometto, M. G., Park, G. I. & Moin, P. 2020 Non-equilibrium three-dimensional boundary layers at moderate Reynolds numbers. J. Fluid Mech. 833, A20.CrossRefGoogle Scholar
Lund, T. S., Wu, X. & Squires, K. D. 1998 Generation of turbulent inflow data for spatially-developing boundary layer simulation. J. Comput. Phys. 140, 233–258.CrossRefGoogle Scholar
Marusic, I., Monty, J. P., Hultmark, M. & Smits, A. J. 2013 On the logarithmic region in wall turbulence. J. Fluid Mech. 716, R3.CrossRefGoogle Scholar
Menter, F. R. 1994 Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 32 (8), 1598–1605.CrossRefGoogle Scholar
McLean, D. J. 2013 Understanding Aerodynamics – Arguing from the Real Physics. Wiley.Google Scholar
Moin, P., Shih, T. H., Driver, D. & Mansour, N. N. 1990 Direct numerical simulation of a three-dimensional turbulent boundary layer. Phys. Fluids A 2, 1846–1853.CrossRefGoogle Scholar
Morinishi, Y., Lund, T. S., Vasilyev, O. V. & Moin, P. 1998 Fully conservative higher order finite difference schemes for incompressible flow. J. Comput. Phys. 143, 90–124.CrossRefGoogle Scholar
Nickels, T. B., Marusic, I., Hafez, S., Hutchins, N. & Chong, M. S. 2007 Some predictions of the attached eddy model for a high Reynolds number boundary layer. Phil. Trans. R. Soc. A 365, 807–822.CrossRefGoogle ScholarPubMed
Ӧlcmen, S. M. & Simpson, R. L. 1993 Evaluation of algebraic eddy-viscosity models in three-dimensional turbulent boundary layer flows. AIAA J. 31, 1545–1554.CrossRefGoogle Scholar
Ӧlcmen, S. M. & Simpson, R. L. 1995 An experimental study of a three-dimensional pressure-driven turbulent boundary layer. J. Fluid Mech. 290, 225–262.CrossRefGoogle Scholar
Pierce, F. J. & McAllister, J. E. 1983 Near-wall similarity in a shear-driven three-dimensional turbulent boundary layer. Trans. ASME: J. Fluids Engng 105, 263–269.Google Scholar
Renard, N. & Deck, S. 2016 A theoretical decomposition of mean skin friction generation into physical phenomena across the boundary layer. J. Fluid Mech. 790, 339–367.CrossRefGoogle Scholar
Rotta, J. C. 1962 Turbulent boundary layers in incompressible flow. Prog. Aeronaut. Sci. 2, 1–219.CrossRefGoogle Scholar
Rotta, J. C. 1979 A family of turbulence models for three-dimensional boundary layers. In Turbulent Shear Flows I (ed. Durst, F., Launder, B. E., Schmidt, F. W. & Whitelaw, J. H.), pp. 267–278. Springer.CrossRefGoogle Scholar
Schlatter, P. & Brandt, L. 2010 DNS of spatially-developing three-dimensional boundary layers. In Direct and Large-Eddy Simulation VII (ed. Armenio, V., Geurts, B. & Fröhlich, J.), pp. 57–63. Springer.Google Scholar
Schlatter, P. & Örlü, R. 2010 Assessment of direct numerical simulation data of turbulent boundary layers. J. Fluid Mech. 659, 116–126.CrossRefGoogle Scholar
Sendstad, O. & Moin, P. 1992 The near wall mechanics of three-dimensional turbulent boundary layers. Rep. TF-57. Thermosciences Division, Department of Mechanical Engineering, Stanford University.Google Scholar
Simens, M. P., Jimenez, J., Hoyas, S. & Mizuno, Y. 2009 A high-resolution code for turbulent boundary layers. J. Comput. Phys. 228, 4218–4231.CrossRefGoogle Scholar
Smits, A. J., Matheson, N. & Joubert, P. N. 1983 Low-Reynolds-number turbulent boundary layers in zero and favourable pressure gradients. J. Ship Res. 27, 147–157.Google Scholar
Spalart, P. R. 1988 Direct simulation of a turbulent boundary layer up to ${R_\theta } = 1410$. J. Fluid Mech. 187, 61–98.CrossRefGoogle Scholar
Spalart, P. R. 1989 Theoretical and numerical study of a three-dimensional turbulent boundary layer. J. Fluid Mech. 205, 319–340.CrossRefGoogle Scholar
Spalart, P. R. & Allmaras, S. R. 1994 A one-equation turbulence model for aerodynamic flows. Rech. Aerosp. 1, 5–21.Google Scholar
Spalart, P. R. & Strelets, M. 2000 Mechanisms of transition and heat transfer in a separation bubble. J. Fluid Mech. 403, 329–349.CrossRefGoogle Scholar
Spalart, P. R., Strelets, M. & Travin, A. 2006 Direct numerical simulation of large-eddy-break-up devices in a boundary layer. Int. J. Heat Fluid Flow 27, 902–910.CrossRefGoogle Scholar
Spalart, P. R. & Watmuff, J. H. 1993 Experimental and numerical study of a turbulent boundary layer with pressure gradients. J. Fluid Mech. 249, 337–371.CrossRefGoogle Scholar
Tomkins, C. D. & Adrian, R. J. 2005 Energetic spanwise modes in the logarithmic layer of a turbulent boundary layer. J. Fluid Mech. 545, 141–162.CrossRefGoogle Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow, vol. 2. Cambridge University Press.Google Scholar
Wei, T. 2018 Integral properties of turbulent-kinetic-energy production and dissipation in turbulent wall-bounded flows. J. Fluid Mech. 854, 449–473.CrossRefGoogle Scholar
White, F. M. 1991 Viscous Fluid Flow, 3rd edn. McGraw-Hill.Google Scholar
Wu, X. & Moin, P. 2009 Direct numerical simulation of turbulence in a nominally-zero-pressure-gradient flat-plate boundary layer. J. Fluid Mech. 630, 5–41.CrossRefGoogle Scholar
Wu, X. & Squires, K. D. 1997 Large eddy simulation of an equilibrium three-dimensional turbulent boundary layer. AIAA J. 35, 67–74.CrossRefGoogle Scholar