Published online by Cambridge University Press: 27 August 2024
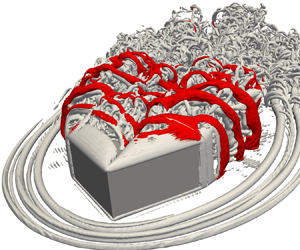
Comprehensive coherent structures around a surface-mounted low aspect ratio square cylinder in uniform flow with an oblique angle of  $45^{\circ }$ were investigated for cylinder-width-based Reynolds numbers of 3000 and 10 000 by direct numerical simulation based on a topology-confined mesh refinement framework. High-resolution simulations and the critical-point concept were scrutinized to reveal for the first time the reasonable and compatible topologies of flow separation and complete near-wall structures, due to their extensive impact on various engineering applications. Large-scale horseshoe vortices are observed at two notable foci in the viscous sublayer. Within this layer, a wall-parallel jet is formed by downflow intruding into the bottom surface at the half-saddle point, then deflecting in the upstream direction and finally penetrating the bottom surface until the half-saddle point. A pair of conical vortices on the cylinder's top surface switch themselves on two sides of the square cylinder, where the switching frequency is identical with that of the sway of the side shear layer. The undulation of the Kelvin–Helmholtz instability is identified in the instantaneous development of a conical vortex and side shear layer, where the scaling of the ratio of the Kelvin–Helmholtz and von Kármán frequencies follows the power-law relation obtained by Lander et al. (J. Fluid Mech., vol. 849, 2018, pp. 1096–1119). Large-scale arch-shaped vortex is often detected in the intermediate wake region of a square cylinder, involving two interconnected portions, such as the leg portion separated from leeward surfaces and head portion rolled up from the top surface. The leg portion of the arch-shaped vortex was rooted by two foci near the bottom-surface plane.
$45^{\circ }$ were investigated for cylinder-width-based Reynolds numbers of 3000 and 10 000 by direct numerical simulation based on a topology-confined mesh refinement framework. High-resolution simulations and the critical-point concept were scrutinized to reveal for the first time the reasonable and compatible topologies of flow separation and complete near-wall structures, due to their extensive impact on various engineering applications. Large-scale horseshoe vortices are observed at two notable foci in the viscous sublayer. Within this layer, a wall-parallel jet is formed by downflow intruding into the bottom surface at the half-saddle point, then deflecting in the upstream direction and finally penetrating the bottom surface until the half-saddle point. A pair of conical vortices on the cylinder's top surface switch themselves on two sides of the square cylinder, where the switching frequency is identical with that of the sway of the side shear layer. The undulation of the Kelvin–Helmholtz instability is identified in the instantaneous development of a conical vortex and side shear layer, where the scaling of the ratio of the Kelvin–Helmholtz and von Kármán frequencies follows the power-law relation obtained by Lander et al. (J. Fluid Mech., vol. 849, 2018, pp. 1096–1119). Large-scale arch-shaped vortex is often detected in the intermediate wake region of a square cylinder, involving two interconnected portions, such as the leg portion separated from leeward surfaces and head portion rolled up from the top surface. The leg portion of the arch-shaped vortex was rooted by two foci near the bottom-surface plane.