Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Gupta, A.
and
Sbragaglia, M.
2014.
Deformation and breakup of viscoelastic droplets in confined shear flow.
Physical Review E,
Vol. 90,
Issue. 2,
Zarghami, A.
Falcucci, G.
Jannelli, E.
Succi, S.
Porfiri, M.
and
Ubertini, S.
2014.
Lattice Boltzmann modeling of water entry problems.
International Journal of Modern Physics C,
Vol. 25,
Issue. 12,
p.
1441012.
De Rosis, Alessandro
2014.
A lattice Boltzmann model for multiphase flows interacting with deformable bodies.
Advances in Water Resources,
Vol. 73,
Issue. ,
p.
55.
Kähler, G.
Bonelli, F.
Gonnella, G.
and
Lamura, A.
2015.
Cavitation inception of a van der Waals fluid at a sack-wall obstacle.
Physics of Fluids,
Vol. 27,
Issue. 12,
Dorschner, B.
Bösch, F.
Chikatamarla, S. S.
Boulouchos, K.
and
Karlin, I. V.
2016.
Entropic multi-relaxation time lattice Boltzmann model for complex flows.
Journal of Fluid Mechanics,
Vol. 801,
Issue. ,
p.
623.
Falcucci, Giacomo
Succi, Sauro
Montessori, Andrea
Melchionna, Simone
Prestininzi, Pietro
Barroo, Cedric
Bell, David C.
Biener, Monika M.
Biener, Juergen
Zugic, Branko
and
Kaxiras, Efthimios
2016.
Mapping reactive flow patterns in monolithic nanoporous catalysts.
Microfluidics and Nanofluidics,
Vol. 20,
Issue. 7,
Russo, S.
Krastev, V. K.
Jannelli, E.
and
Falcucci, G.
2016.
Design and optimization of an experimental test bench for the study of impulsive fluid-structure interactions.
Vol. 1738,
Issue. ,
p.
270020.
Krastev, Vesselin Krassimirov
Amati, Giorgio
Jannelli, Elio
and
Falcucci, Giacomo
2016.
Direct Numerical Simulation of SCR Reactors through Kinetic Approach.
Vol. 1,
Issue. ,
Falcucci, Giacomo
Amati, Giorgio
Krastev, Vesselin K.
Montessori, Andrea
Yablonsky, Grigoriy S.
and
Succi, Sauro
2017.
Heterogeneous catalysis in pulsed-flow reactors with nanoporous gold hollow spheres.
Chemical Engineering Science,
Vol. 166,
Issue. ,
p.
274.
Lin, Chuandong
Xu, Aiguo
Zhang, Guangcai
Luo, Kai Hong
and
Li, Yingjun
2017.
Discrete Boltzmann modeling of Rayleigh-Taylor instability in two-component compressible flows.
Physical Review E,
Vol. 96,
Issue. 5,
Ezzatneshan, Eslam
2017.
Study of surface wettability effect on cavitation inception by implementation of the lattice Boltzmann method.
Physics of Fluids,
Vol. 29,
Issue. 11,
Wang, Zhaohui
Chen, Si
and
Deng, Xiaogang
2017.
Research on modified cavitation model for self-excited oscillation pulsed jet nozzle.
p.
90.
Gou, Xiang
Li, Yamei
Zhang, Qiyan
Shah, Imran
Zhao, Dong
Liu, Shian
Wang, Yating
Wang, Enyu
and
Wu, Jinxiang
2017.
A Novel Semi-Visualizable Experimental Study of a Plate Gravity Heat Pipe at Unsteady State.
Energies,
Vol. 10,
Issue. 12,
p.
1994.
Seager, R. J.
Acevedo, Andrew J.
Spill, Fabian
and
Zaman, Muhammad H.
2018.
Solid dissolution in a fluid solvent is characterized by the interplay of surface area-dependent diffusion and physical fragmentation.
Scientific Reports,
Vol. 8,
Issue. 1,
Krastev, Vesselin K.
Amati, Giorgio
Succi, Sauro
and
Falcucci, Giacomo
2018.
On the effects of surface corrugation on the hydrodynamic performance of cylindrical rigid structures.
The European Physical Journal E,
Vol. 41,
Issue. 8,
Sofonea, V.
Biciuşcă, T.
Busuioc, S.
Ambruş, Victor E.
Gonnella, G.
and
Lamura, A.
2018.
Corner-transport-upwind lattice Boltzmann model for bubble cavitation.
Physical Review E,
Vol. 97,
Issue. 2,
Decent, S. P.
Părău, E. I.
Simmons, M. J. H.
and
Uddin, J.
2018.
On mathematical approaches to modelling slender liquid jets with a curved trajectory.
Journal of Fluid Mechanics,
Vol. 844,
Issue. ,
p.
905.
Liu, Haihu
Ba, Yan
Wu, Lei
Li, Zhen
Xi, Guang
and
Zhang, Yonghao
2018.
A hybrid lattice Boltzmann and finite difference method for droplet dynamics with insoluble surfactants.
Journal of Fluid Mechanics,
Vol. 837,
Issue. ,
p.
381.
Montessori, A.
Halliday, I.
Lauricella, M.
Lishchuk, S.V.
Pontrelli, G.
Spencer, T.J.
and
Succi, S.
2018.
Numerical Methods and Advanced Simulation in Biomechanics and Biological Processes.
p.
357.
Peng, Chi
Tian, Shouceng
Li, Gensheng
and
Sukop, Michael C.
2018.
Single-component multiphase lattice Boltzmann simulation of free bubble and crevice heterogeneous cavitation nucleation.
Physical Review E,
Vol. 98,
Issue. 2,
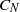 ${C}_{N} $) proves to be a poor predictor of the onset of cavitation. Finally, strong dependence of the bubble morphology on the surface tension is also highlighted.
${C}_{N} $) proves to be a poor predictor of the onset of cavitation. Finally, strong dependence of the bubble morphology on the surface tension is also highlighted.

