Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-29T13:32:37.206Z Has data issue: false hasContentIssue false
  • English
  • Français

Direct measurement of the Sears function in turbulent flow

Published online by Cambridge University Press:  29 May 2018

Mingshui Li ,
Yang Yang Open the ORCID record for Yang Yang [Opens in a new window] ,
Ming Li  and
Haili Liao
Mingshui Li
Affiliation:
Research Centre for Wind Engineering, Southwest Jiaotong University, Chengdu 610031, China Key Laboratory for Wind Engineering of Sichuan Province, Chengdu 610031, China
Yang Yang*
Affiliation:
Research Centre for Wind Engineering, Southwest Jiaotong University, Chengdu 610031, China
Ming Li
Affiliation:
Research Centre for Wind Engineering, Southwest Jiaotong University, Chengdu 610031, China
Haili Liao
Affiliation:
Research Centre for Wind Engineering, Southwest Jiaotong University, Chengdu 610031, China Key Laboratory for Wind Engineering of Sichuan Province, Chengdu 610031, China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The applicability of the strip assumption in the estimation of the unsteady lift response of a two-dimensional wing in turbulent flow is investigated. The ratio between the lift spectrum calculated from the two-wavenumber analysis and the lift spectrum calculated from the strip assumption is used to evaluate the accuracy of the strip assumption. It is shown that the accuracy of the strip assumption is controlled by the ratio of the turbulence integral scale to the chord and the aspect ratio. With an increase of these two parameters, the ratio for evaluating the accuracy of the strip assumption increases, the one-wavenumber transfer function obtained from the strip assumption approaches the Sears function gradually. When these two parameters take suitable values, the strip assumption could be applicable to the calculation of the unsteady lift on a wing in turbulent flow. Here, the term aspect ratio refers to the ratio of the specified span (an finite spanwise length of the two-dimensional wing) to the chord, the unsteady lift is calculated over this specified spanwise length. The theoretical analysis is verified by means of force measurement experiments conducted in a wind tunnel. In the experiment, a square passive grid is installed downstream of the entrance of the test section to generate approximately homogeneous and isotropic turbulence. 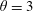Three rectangular wings with different aspect ratios ($\unicode[STIX]{x1D703}=3$, 5 and 7) are used. These wing models have an NACA 0015 profile cross-section and a fixed chord length 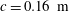$c=0.16~\text{m}$. The testing results show that, at a fixed ratio of turbulence integral scale to chord, the deviation between the experimental one-wavenumber transfer function obtained from the strip assumption and the Sears function is reduced with increasing aspect ratio, as expected by the theoretical predictions. However, due to the effect of thickness, the experimental values at high frequencies cannot be captured by the Sears function which is derived based on the flat plate assumption. In practical applications, the effect of thickness on the transfer function should be considered.

JFM classification

Aerodynamics: Aerodynamics Aerodynamics: Flow-structure interactions Turbulent Flows: Turbulent Flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 847 , 25 July 2018 , pp. 768 - 785
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Atassi, H. M. 1984 The Sears problem for a lifting airfoil revisited – new results. J. Fluid Mech. 141, 109–122.Google Scholar
Blake, W. K. 1986 Mechanics of Flow-Induced Sound and Vibration. Academic Press.Google Scholar
Comte-Bellot, G. & Corrsin, S. 1966 The use of a contraction to improve the isotropy of grid-generated turbulence. J. Fluid Mech. 25, 657–682.CrossRefGoogle Scholar
Cordes, U., Kampers, G., Meißner, T., Tropea, C., Peinke, J. & Hölling, M. 2017 Note on the limitations of the Theodorsen and Sears functions. J. Fluid Mech. 811, R1.CrossRefGoogle Scholar
Davidson, P. A. 2004 Turbulence: An Introduction for Scientists and Engineers. Oxford University Press.Google Scholar
Devenport, W., Staubs, J. K. & Glegg, S. A. L. 2010 Sound radiation from real airfoils in turbulence. J. Sound Vib. 329, 3470–3483.Google Scholar
Filotas, L. T.1969 Theory of airfoil response in a gusty atmosphere. Part I – aerodynamic transfer function. Tech. Rep. 139. UTIAS.Google Scholar
Filotas, L. T. 1971 Approximate transfer functions for large aspect ratio wings in turbulent flow. J. Aircraft 8, 395–400.CrossRefGoogle Scholar
Gershfeld, J. 2004 Leading edge noise from thick foils in turbulent flows. J. Acoust. Soc. Am. 116, 1416–1426.Google Scholar
Glegg, S. A. L. & Devenport, W. 2009 Unsteady loading on an airfoil of arbitrary thickness. J. Sound Vib. 319, 1252–1270.CrossRefGoogle Scholar
Goldstein, M. E. & Atassi, H. M. 1976 A complete second-order theory for the unsteady flow about an airfoil due to a periodic gust. J. Fluid Mech. 74, 741–765.Google Scholar
Graham, J. M. R. 1970 Lifting-surface theory for the problem of an arbitrary yawed sinusoidal gust incident on a thin aerofoil in incompressible flow. Aeronaut. Q. 21, 182–198.CrossRefGoogle Scholar
Graham, J. M. R. 1971 A lift-surface theory for the rectangular wing in non-stationary flow. Aeronaut. Q. 22, 83–100.Google Scholar
Jackson, R., Graham, J. M. R. & Maull, D. J. 1973 The lift on a wing in a turbulent flow. Aeronaut. Q. 24, 155–166.Google Scholar
Kitamura, T., Nagata, K., Sakai, Y. & Harasaki, T. 2014 On invariants in grid turbulence at moderate Reynolds numbers. J. Fluid Mech. 738, 378–406.CrossRefGoogle Scholar
Lamson, P.1957 Measurements of lift fluctuations due to turbulence. NACA Tech. Rep. 3880.Google Scholar
Larose, G. L. 1999 Experimenter determination of the aerodynamic admittance of a bridge deck segment. J. Fluids Struct. 13, 1029–1040.Google Scholar
Larose, G. L. & Mann, J. 1998 Gust loading on streamlined bridge decks. J. Fluids Struct. 12, 511–536.Google Scholar
Lavoie, P., Djenidi, L. & Antonia, R. A. 2007 Effects of initial conditions in decaying turbulence generated by passive grids. J. Fluid Mech. 585, 395–420.Google Scholar
Li, S. & Li, M. 2017 Spectral analysis and coherence of aerodynamic lift on rectangular cylinders in turbulent flow. J. Fluid Mech. 830, 408–438.CrossRefGoogle Scholar
Li, S., Li, M. & Liao, H. 2015 The lift on an aerofoil in grid-generated turbulence. J. Fluid Mech. 71, 16–35.Google Scholar
Liepmann, H. W. 1952 On the application of statistical concepts to buffeting problem. J. Aero. Sci. 19, 793–800.Google Scholar
Lysak, P. D., Capone, D. E. & Jonson, M. L. 2013 Prediction of high frequency gust response with airfoil thickness effects. J. Fluids Struct. 39, 258–274.CrossRefGoogle Scholar
Lysak, P. D., Capone, D. E. & Jonson, M. L. 2016 Measurement of the unsteady lift of thick airfoils in incompressible turbulent flow. J. Fluids Struct. 66, 315–330.Google Scholar
Ma, C.2007 3D Aerodynamic admittance research of streamlined box bridge decks. PhD thesis, Southwest Jiaotong University.Google Scholar
Massaro, M. & Graham, J. M. R. 2015 The effect of three-dimensionality on the aerodynamic admittance of thin sections in free stream turbulence. J. Fluids Struct. 57, 81–89.CrossRefGoogle Scholar
Mugridge, B. D. 1971 Gust loading on a thin aerofoil. Aeronaut. Q. 22, 301–310.CrossRefGoogle Scholar
Nagata, K., Hunt, J. C. R., Sakai, Y. & Wong, H. 2011 Distorted turbulence and secondary flow near right-angled plates. J. Fluid Mech. 668, 446–479.CrossRefGoogle Scholar
Ribner, H. S. 1956 Spectral theory of buffeting and gust response: unification and extension. J. Aero. Sci. 23, 1075–1077.Google Scholar
Roberts, J. B. & Surry, D. 1973 Coherence of grid-generated turbulence. J. Engng Mech. Div. 99, 1227–1245.Google Scholar
Santana, L. D., Christophe, J., Schram, C. & Desmet, W. 2016 A rapid distortion theory modified turbulence spectra for semi-analytical airfoil noise prediction. J. Sound Vib. 383, 349–363.CrossRefGoogle Scholar
Sears, R. W.1938 A systematic presentation of the theory of thin airfoils in non-uniform motion. PhD thesis, California Institute of Technology.Google Scholar