Published online by Cambridge University Press: 18 July 2019
The dynamics of ideally polarizable spherical particles in concentrated suspensions under the effects of nonlinear electrokinetic phenomena is analysed using large-scale numerical simulations. Particles are assumed to carry no net charge and considered to undergo the combination of dielectrophoresis and induced-charge electrophoresis termed dipolophoresis. Chaotic motion and resulting hydrodynamic diffusion are known to be driven by the induced-charge electrophoresis, which dominates the dielectrophoresis. Up to a volume fraction 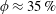 $\unicode[STIX]{x1D719}\approx 35\,\%$, the particle dynamics seems to be hindered by the increase in the magnitude of excluded volume interactions with concentration. However, a non-trivial suspension behaviour is observed in concentrated regimes, where the hydrodynamic diffusivity starts to increase with the volume fraction at
$\unicode[STIX]{x1D719}\approx 35\,\%$, the particle dynamics seems to be hindered by the increase in the magnitude of excluded volume interactions with concentration. However, a non-trivial suspension behaviour is observed in concentrated regimes, where the hydrodynamic diffusivity starts to increase with the volume fraction at 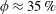 $\unicode[STIX]{x1D719}\approx 35\,\%$, before reaching a local maximum, and then drastically decreases on approaching random close packing. Similar non-trivial behaviours are observed in the particle velocity and number-density fluctuations around volume fractions at which the non-trivial behaviour of the hydrodynamic diffusion is observed. We explain these non-trivial behaviours as a consequence of particle contacts, which are related to the dominant mechanism of particle pairings. The particle contacts are classified into attractive and repulsive classes by the nature of contacts, and in particular, the strong repulsive contact becomes predominant at
$\unicode[STIX]{x1D719}\approx 35\,\%$, before reaching a local maximum, and then drastically decreases on approaching random close packing. Similar non-trivial behaviours are observed in the particle velocity and number-density fluctuations around volume fractions at which the non-trivial behaviour of the hydrodynamic diffusion is observed. We explain these non-trivial behaviours as a consequence of particle contacts, which are related to the dominant mechanism of particle pairings. The particle contacts are classified into attractive and repulsive classes by the nature of contacts, and in particular, the strong repulsive contact becomes predominant at 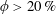 $\unicode[STIX]{x1D719}>20\,\%$. Moreover, this transition is visible in the pair distribution functions, which also reveal the change in the suspension microstructure in concentrated regimes. It appears that strong and massive repulsive contacts along the direction perpendicular to an electric field promote the non-trivial suspension behaviours observed in concentrated regimes.
$\unicode[STIX]{x1D719}>20\,\%$. Moreover, this transition is visible in the pair distribution functions, which also reveal the change in the suspension microstructure in concentrated regimes. It appears that strong and massive repulsive contacts along the direction perpendicular to an electric field promote the non-trivial suspension behaviours observed in concentrated regimes.
Dynamics in a suspension undergoing dipolophoresis (combination of dielectrophoresis and induced-charge electrophoresis) under a uniform external electric field, in a periodic box of dimensions 20 x 20 x 20 and at a volume fraction of 10%. The electric field points in the vertical direction. The occasional particle flickers are a consequence of the periodic boundary conditions, by which a particle leaving the simulation box immediately reenters on the other side.
Dynamics in a suspension undergoing dipolophoresis (combination of dielectrophoresis and induced-charge electrophoresis) under a uniform external electric field, in a periodic box of dimensions 20 x 20 x 20 and at a volume fraction of 25%. The electric field points in the vertical direction. The occasional particle flickers are a consequence of the periodic boundary conditions, by which a particle leaving the simulation box immediately reenters on the other side.
Dynamics in a suspension undergoing dipolophoresis (combination of dielectrophoresis and induced-charge electrophoresis) under a uniform external electric field, in a periodic box of dimensions 20 x 20 x 20 and at a volume fraction of 45%. The electric field points in the vertical direction. The occasional particle flickers are a consequence of the periodic boundary conditions, by which a particle leaving the simulation box immediately reenters on the other side.
Dynamics in a suspension undergoing dipolophoresis (combination of dielectrophoresis and induced-charge electrophoresis) under a uniform external electric field, in a periodic box of dimensions 20 x 20 x 20 and at a volume fraction of 59%. The electric field points in the vertical direction. The occasional particle flickers are a consequence of the periodic boundary conditions, by which a particle leaving the simulation box immediately reenters on the other side.