Hostname: page-component-745bb68f8f-mzp66 Total loading time: 0 Render date: 2025-01-08T10:31:34.766Z Has data issue: false hasContentIssue false
  • English
  • Français

Diffusiophoresis of colloidal particles in neutral solute gradients at finite Péclet number

Published online by Cambridge University Press:  14 August 2013

Aditya S. Khair
Aditya S. Khair*
Affiliation:
Department of Chemical Engineering, Carnegie Mellon University, Pittsburgh, PA 15213, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The role of neutral solute advection on the diffusiophoretic motion of colloidal particles is quantified. Theoretical analyses of this phenomenon usually assume that the solute concentration evolves solely via diffusion; that is, the Péclet number (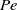$\mathit{Pe}$) for solute transport is identically zero. This leads to the conclusion that the translational diffusiophoretic velocity of a colloid is independent of its size, shape, and orientation with respect to the imposed solute gradient, provided that the colloid has uniform surface properties and that the length scale of interaction between the solute and the particle surface is much smaller than the particle size (Morrison, J. Colloid Interface Sci. vol. 34, 1970, p. 210). For a single spherical colloid, we show that the particle velocity decreases monotonically with increasing 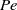$\mathit{Pe}$. Moreover, the solute concentration and fluid flow around the colloid become markedly fore–aft asymmetric as 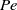$\mathit{Pe}$ is increased. Next, an asymptotic expansion at small 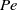$\mathit{Pe}$ predicts that solute advection leads to relative phoretic motion between two identical spherical colloids, which ultimately align in a plane normal to the imposed gradient (there is no relative motion at 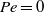$\mathit{Pe}= 0$). Finally, asymptotic analysis of the diffusiophoretic motion of a slightly non-spherical colloid at small 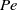$\mathit{Pe}$ demonstrates that advection leads to a shape- and orientation-dependent particle velocity, in contrast to the insensitivity of the velocity to shape and orientation at $\mathit{Pe}= 0$.

JFM classification

Complex Fluids: Colloids Low-Reynolds-number flows: Low-Reynolds-number flows Micro-/Nano-fluid dynamics: Micro-/Nano-fluid dynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 731 , 25 September 2013 , pp. 64 - 94
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abécassis, B., Cottin-Bizonne, C., Ybert, C., Ajdari, A. & Bocquet, L. 2008 Boosting migration of large particles by solute contrasts. Nat. Mater. 7, 785–789.CrossRefGoogle ScholarPubMed
Acrivos, A., Jeffrey, D. J. & Saville, D. A. 1990 Particle migration in suspensions by thermocapillary or electrophoretic motion. J. Fluid Mech. 212, 95–110.CrossRefGoogle Scholar
Acrivos, A. & Taylor, T. D. 1962 Heat and mass transfer from single spheres in Stokes flow. Phys. Fluids 5, 387–394.Google Scholar
Acrivos, A. & Taylor, T. D. 1964 The Stokes flow past an arbitrary particle. Chem. Engng Sci. 19, 445–451.Google Scholar
Alexander, G. P. & Liu, A. J. 2011 Self-diffusiophoresis in the advection dominated regime. arXiv:1107.3581.Google Scholar
Anderson, J. L. 1983 Movement of a semipermeable vesicle through an osmotic gradient. Phys. Fluids 26, 2871–2879.Google Scholar
Anderson, J. L. 1989 Colloid transport by interfacial forces. Annu. Rev. Fluid Mech. 21, 61–99.Google Scholar
Anderson, J. L. & Prieve, D. C. 1984 Diffusiophoresis: migration of colloidal particles in gradients of solute concentration. Sep. Purif. Rev. 13, 67–103.CrossRefGoogle Scholar
Anderson, J. L. & Prieve, D. C. 1991 Diffusiophoresis caused by gradients of strongly adsorbing solutes. Langmuir. 7, 403–406.Google Scholar
Balasubramaniam, R. & Subramanian, R. S. 1996 Thermocapillary bubble migration: thermal boundary layers for large Marangoni numbers. Intl J. Multiphase Flow 22, 593–612.Google Scholar
Banigan, E. J., Gelbart, M. A., Gitai, Z., Wingreen, N. S. & Liu, A. J. 2011 Filament depolymerization can explain chromosome pulling during bacterial mitosis. PLoS Comput. Biol. 7, 1–11.CrossRefGoogle ScholarPubMed
Braibanti, M., Vigolo, D. & Piazza, R. 2008 Does thermophoretic mobility depend on particle size? Phys. Rev. Lett. 100, 108303.Google Scholar
Brenner, H. 1964a The Stokes resistance of a slightly deformed sphere. Chem. Engng Sci. 19, 519–539.Google Scholar
Brenner, H. 1964b The Stokes resistance of an arbitrary particle. Part 4. Arbitrary fields of flow. Chem. Engng Sci. 19, 703–727.Google Scholar
Ebbens, S. & Howse, J. R. 2010 In pursuit of propulsion at the nanoscale. Soft Matt. 6, 726–738.Google Scholar
Ebbens, S., Tu, M-H., Howse, J. R. & Golestanian, R. 2012 Size dependence of the propulsion velocity for catalytic Janus-sphere swimmers. Phys. Rev. E 85, 020401.CrossRefGoogle ScholarPubMed
Golestanian, R., Liverpool, T. B. & Ajdari, A. 2007 Designing phoretic micro- and nano-swimmers. New J. Phys. 9, 126.Google Scholar
Howse, J. R., Jones, R. A., Ryan, A. J., Gough, T., Vafabaksh, & Golestanian, R. 2007 Self-motile colloidal particles: from directed propulsion to random walk. Phys. Rev. Lett. 99, 048102.Google Scholar
Jeffrey, D. J. 1973 Conduction through a random suspension of spheres. Proc. R. Soc. A 335, 355–367.Google Scholar
Keh, H. J. & Weng, J. C. 2001 Diffusiophoresis of colloidal spheres in non electrolyte gradients at small but finite Péclet numbers. Colloid Polym. Sci. 279, 305–311.CrossRefGoogle Scholar
Khair, A. S. & Brady, J. F. 2006 Single particle motion in colloidal dispersions: a simple model for active and nonlinear microrheology. J. Fluid Mech. 557, 73–117.CrossRefGoogle Scholar
Leal, L. G. 1980 Particle motions in a viscous fluid. Annu. Rev. Fluid Mech. 12, 435–476.CrossRefGoogle Scholar
Lee, K-C. & Liu, A. J. 2008 New proposed mechanism of Actin-polymerization-driven motility. Biophys. J. 95, 4529–4539.Google Scholar
Lee, K-C. & Liu, A. J. 2009 Force–velocity relation for Actin-polymerization-driven motility from Brownian dynamics simulations. Biophys. J. 97, 1295–1304.Google Scholar
Leshansky, A. M., Lavrenteva, O. M. & Nir, A. 2001 Thermocapillary migration of bubbles: convective effects at low Péclet number. J. Fluid Mech. 443, 377–401.CrossRefGoogle Scholar
Leshansky, A. M. & Nir, A. 2001 Thermocapillary alignment of gas bubbles induced by convective transport. J. Colloid Interface Sci. 240, 544–551.Google Scholar
Magar, V., Goto, T. & Pedley, T. J. 2003 Nutrient uptake by a self-propelled steady squirmer. Q. J. Mech. Appl. Maths 56, 65–91.Google Scholar
McNab, G. S. & Meisen, A. 1973 Thermophoresis in liquids. J. Colloid Interface Sci. 44, 339–346.Google Scholar
Michelin, S. & Lauga, E. 2011 Optimal feeding is optimal swimming for all Péclet numbers. Phys. Fluids 23, 101901.CrossRefGoogle Scholar
Mohan, A. & Brenner, H. 2006 Thermophoretic motion of a slightly deformed sphere through a viscous fluid. SIAM J. Appl. Maths 66, 787–801.Google Scholar
Morrison, F. A. 1970 Electrophoresis of a particle of arbitrary shape. J. Colloid Interface Sci. 34, 210–214.Google Scholar
Parola, A. & Piazza, R. 2004 Particle thermophoresis in liquids. Eur. Phys. J. E 15, 255–263.Google Scholar
Prieve, D. C., Anderson, J. L., Ebel, J. P. & Lowell, M. E. 1984 Motion of a particle generated by chemical gradients. Part 2. Electrolytes. J. Fluid Mech. 148, 247–269.CrossRefGoogle Scholar
Reed, A. M. & Morrison, F. A. 1976 Hydrodynamic interactions in electrophoresis. J. Colloid Interface Sci. 54, 117–133.Google Scholar
Saville, D. A. 1977 Electrokinetic effects with small particles. Annu. Rev. Fluid Mech. 9, 321–337.CrossRefGoogle Scholar
Schnitzer, O. & Yariv, E. 2012 Macroscale description of electrokinetic flows at large zeta potentials: nonlinear surface conduction. Phys. Rev. E 86, 021503.Google Scholar
Schnitzer, O., Zeyde, R., Yavneh, I. & Yariv, E. 2013 Weakly nonlinear electrophoresis of a highly charged colloidal particle. Phys. Fluids 25, 052004.CrossRefGoogle Scholar
Sellier, A. 1999 Sur l’électrophorèse d’un ensemble de particules portant la même densiteé uniform de charges. C. R. Acad. Sci. Paris. 327, 443–448.Google Scholar
Squires, T. M. & Quake, S. R. 2005 Microfluidics: fluid physics at the nanoliter scale. Rev. Mod. Phys. 77, 977–1026.Google Scholar
Staffield, P. O. & Quinn, J. A. 1989 Diffusion-induced banding of colloid particles via diffusiophoresis. J. Colloid Interface Sci. 130, 88–100.Google Scholar
Stone, H. A. & Samuel, A. D. T. 1996 Propulsion of microorganisms by surface distortions. Phys. Rev. Lett. 77, 4102–4104.Google Scholar
Subramanian, R. S. 1981 Slow migration of a gas bubble in a thermal gradient. AIChE J. 27, 646–654.Google Scholar
Yariv, E. 2004 Inertia-induced electrophoretic interactions. Phys. Fluids 16, L24–L27.CrossRefGoogle Scholar
Yariv, E. 2006 Force-free electrophoresis? Phys. Fluids 18, 031702.Google Scholar
Yariv, E. 2008 Thermophoresis due to strong temperature gradients. SIAM J. Appl. Maths 69, 453–472.Google Scholar
Zheng, F. 2002 Thermophoresis of spherical and non-spherical particles: a review of theories and experiments. Adv. Colloid Interface Sci. 97, 255–278.Google Scholar
Zukoski, C. F. & Saville, D. A. 1987 Electrokinetic properties of particles in concentrated suspensions. J. Colloid Interface Sci. 115, 422–436.Google Scholar