Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-05T06:59:33.412Z Has data issue: false hasContentIssue false
  • English
  • Français

Development of turbulent boundary layers past a step change in wall roughness

Published online by Cambridge University Press:  19 April 2016

R. E. Hanson  and
B. Ganapathisubramani
R. E. Hanson
Affiliation:
Faculty of Engineering and the Environment, University of Southampton, UK
B. Ganapathisubramani*
Affiliation:
Faculty of Engineering and the Environment, University of Southampton, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

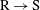In this study, the development of a boundary layer past a change in surface roughness (from rough to smooth, $\text{R}\rightarrow \text{S}$) is examined. Measurements of the flow were made by hot wires, whereas the friction velocity was estimated by Preston tube measurements. By means of a diagnostic plot of the turbulence intensity, it is shown that above the internal layer the flow exhibits characteristics of a rough, wall-bounded flow, whereas near the wall the turbulence intensity is similar to that of an isolated smooth wall. Similarly, viscous scaling of the mean streamwise velocity shows an excessive wake region downstream of the 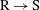$\text{R}\rightarrow \text{S}$ wall surface change that diminishes with the fetch from the surface change. Above the internal layer a second peak in the streamwise Reynolds stress was associated with the upstream rough-wall flow. Examination of the turbulent spectra revealed the presence of large-scale motions within this region that gradually diminish in strength with increasing distance from the change in surface roughness. The magnitude of the near-wall peak failed to collapse to that of a comparable smooth-wall boundary layer under viscous scaling, however, the wall-normal location of the peak appears to be at 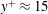$y^{+}\approx 15$ at all downstream distances. A new mixed scaling is proposed for the near-wall peak based on the corrected wake deficit and the friction velocity. This shows the importance of outer region to the growth of near-wall peak in this non-equilibrium boundary layer.

JFM classification

Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 795 , 25 May 2016 , pp. 494 - 523
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alfredsson, P. H., Örlü, R. & Segalini, A. 2012 A new formulation for the streamwise turbulence intensity distribution in wall-bounded turbulent flows. Eur. J. Mech. B 36, 167–175.CrossRefGoogle Scholar
Andreopoulos, J. & Wood, D. H. 1982 The response of a turbulent boundary layer to a short length of surface roughness. J. Fluid Mech. 118, 143–164.CrossRefGoogle Scholar
Antonia, R. A. & Luxton, R. E. 1971 The response of a turbulent boundary layer to a step change in surface roughness. Part 1. Smooth to rough. J. Fluid Mech. 48, 721–761.CrossRefGoogle Scholar
Antonia, R. A. & Luxton, R. E. 1972 The response of a turbulent boundary layer to a step change in surface roughness. Part 2. Rough to smooth. J. Fluid Mech. 53, 737–757.CrossRefGoogle Scholar
Birch, D. M. & Morrison, J. F. 2011 Similarity of the streamwise velocity component in very-rough-wall channel flows. J. Fluid Mech. 668, 174–201.CrossRefGoogle Scholar
Bruun, H. H. 1995 Hot Wire Anemometry: Principles and Signal Analysis. Oxford University Press.CrossRefGoogle Scholar
Burattini, P. & Antonia, R. A. 2005 The effect of different x-wire calibration schemes on some turbulence statistics. Exp. Fluids 38, 80–89.CrossRefGoogle Scholar
Castro, I. P. 2007 Rough-wall boundary layers: mean flow universality. J. Fluid Mech. 585, 469–485.CrossRefGoogle Scholar
Castro, I. P. 2013 Outer-layer turbulence intensities in smooth- and rough-wall boundary layers. J. Fluid Mech. 727, 119–131.CrossRefGoogle Scholar
Chamorro, L. P. & Porté-Agel, F. 2009 Velocity and surface shear stress distributions behind a rough-to-smooth surface transition: a simple new model. Boundary-Layer Meteorol. 130, 29–41.CrossRefGoogle Scholar
De Graaff, D. B. & Eaton, J. K. 2000 Reynolds-number scaling of the flat-plate turbulent boundary layer. J. Fluid Mech. 422, 319–346.CrossRefGoogle Scholar
Efros, V. & Krogstad, P.-Å. 2011 Development of a turbulent boundary layer after a step from smooth to rough surface. Exp. Fluids 51, 1563–1575.CrossRefGoogle Scholar
Elliott, W. P. 1958 The growth of the atmospheric internal boundary layer. Trans. Am. Geophys. Union 39, 1048–1054.Google Scholar
Fernholz, H. H. & Finley, P. J. 1996 The incompressible zero-pressure-gradient turbulent boundary layer: an assessment of the data. Prog. Aerosp. Sci. 32, 245–311.CrossRefGoogle Scholar
Flack, K. A., Schultz, M. P. & Shapiro, T. A. 2005 Experimental support for townsend’s Reynolds number similarity hypothesis on rough walls. Phys. Fluids 17 (3), 035102.CrossRefGoogle Scholar
Ganapathisubramani, B., Hutchins, N., Monty, J. P., Chung, D. & Marusic, I. 2012 Amplitude and frequency modulation in wall turbulence. J. Fluid Mech. 712, 61–91.CrossRefGoogle Scholar
Hutchins, N. & Marusic, I. 2007a Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.CrossRefGoogle Scholar
Hutchins, N. & Marusic, I. 2007b Large-scale influences in near-wall turbulence. Phil. Trans. R. Soc. Lond. A 365, 647–664.Google ScholarPubMed
Hutchins, N., Nickels, T. B., Marusic, I. & Chong, M. S. 2009 Hot-wire spatial resolution issues in wall-bounded turbulence. J. Fluid Mech. 635, 103.CrossRefGoogle Scholar
Jacobi, I. & Mckeon, B. J. 2011 New perspectives on the impulsive roughness-perturbation of a turbulent boundary layer. J. Fluid Mech. 677, 179–203.CrossRefGoogle Scholar
Jiménez, J. 2004 Turbulent flows over rough walls. Annu. Rev. Fluid Mech. 36, 173–196.CrossRefGoogle Scholar
Jones, M. B., Marusic, I. & Perry, A. E. 2001 Evolution and structure of sink-flow turbulent boundary layers. J. Fluid Mech. 428, 1–27.CrossRefGoogle Scholar
Ligrani, P. M. & Bradshaw, P. 1987 Spatial resolution and measurement of turbulence in the viscous sublayer using subminiature hot-wire probes. Exp. Fluids 5, 407–417.CrossRefGoogle Scholar
Loureiro, J. B. R., Sousa, F. B. C. C., Zotin, J. L. Z. & Silva Freire, A. P. 2010 The distribution of wall shear stress downstream of a change in roughness. Intl J. Heat Fluid Flow 31 (5), 785–793.CrossRefGoogle Scholar
Marusic, I. & Kunkel, G. J. 2003 Streamwise turbulence intensity formulation for flat-plate boundary layers. Phys. Fluids 15, 2461–2464.CrossRefGoogle Scholar
Miller, I. S., Shah, D. A. & Antonia, R. A. 1987 A constant temperature hot-wire anemometer. J. Phys. E 20 (3), 311.CrossRefGoogle Scholar
Mulhearn, P. J. 1978 A wind-tunnel boundary-layer study of the effects of a surface roughness change: rough to smooth. Boundary-Layer Meteorol. 15, 3–30.CrossRefGoogle Scholar
Nagib, H. M., Chauhan, K. A. & Monkewitz, P. A. 2007 Approach to an asymptotic state for zero pressure gradient turbulent boundary layers. Phil. Trans. R. Soc. Lond. A 365, 755–770.Google Scholar
Österlund, J. M., Johansson, A. V., Nagib, H. M. & Hites, M. H. 2000 A note on the overlap region in turbulent boundary layers. Phys. Fluids 12, 1–4.CrossRefGoogle Scholar
Patel, V. C. 1965 Calibration of the preston tube and limitations on its use in pressure gradients. J. Fluid Mech. 23, 185–208.CrossRefGoogle Scholar
Perry, A. E. & Li, J. D. 1990 Experimental support for the attached-eddy hypothesis in zero-pressure-gradient turbulent boundary layers. J. Fluid Mech. 218, 405–438.CrossRefGoogle Scholar
Savelyev, S. A. & Taylor, P. A. 2005 Internal boundary layers: I. Height formulae for neutral and diabatic flows. Boundary-Layer Meteorol. 115, 1–25.CrossRefGoogle Scholar
Schultz, M. P. & Flack, K. A. 2009 Turbulent boundary layers on a systematically varied rough wall. Phys. Fluids 21, 015104.CrossRefGoogle Scholar
Smits, A. J. & Wood, D. H. 1985 The response of turbulent boundary layers to sudden perturbations. Annu. Rev. Fluid Mech. 17, 321–358.CrossRefGoogle Scholar
Taylor, J. 1997 Introduction to Error Analysis, the Study of Uncertainties in Physical Measurements, 2nd edn. University Science Books.Google Scholar
Taylor, R. P., Taylor, J. K. & Coleman, H. W. 1993 Relation of the turbulent boundary layer after an abrupt change from rough to smooth wall (data bank contribution). J. Fluids Engng 115 (3), 379–382.CrossRefGoogle Scholar
Zagarola, M. V. & Smits, A. J. 1998 Mean-flow scaling of turbulent pipe flow. J. Fluid Mech. 373, 33–79.CrossRefGoogle Scholar