2.1. Conceptual model

Our conceptual model considers a two-dimensional waterbody such as that in figure 1. The basin has minimum and maximum depths of $d$ and $D$, respectively, and horizontal length-scale $\mathcal {L}$, such that the aspect ratio $D/\mathcal {L}\ll 1$. The origin of the coordinate system is located at the left deepest basin level, with the vertical coordinate $z$ positive upward and the horizontal coordinate $x$ positive towards the basin's interior. The top surface (e.g. air–water interface) is stress free, whereas its sloping bottom satisfies no-slip and no-flux boundary conditions (e.g. no heat flux across the sediment–water interface).

The initial water temperature is formed by a stable two-layer distribution, with temperatures higher than the temperature of maximum density, $T_{MD}\approx 3.98\,^{\circ }\textrm {C}$, and a thermocline (pycnocline) located at $h_{m}>d$ beneath the surface. We model the initial thermal stratification by the smooth function

(2.1)\begin{equation} T(x,z,t=0) = T_{b} + \frac{\Delta T}{2}\left\{1 + \textrm{{tanh}}\left(\frac{z-z_{m}}{\delta_{m}}\right)\right\}, \end{equation}

where $T_{b}$ is the bottom temperature in the interior basin, $T_{s} = T_{b}+\Delta T$ is the surface layer temperature, $z_{m}$ is the height of the thermocline and $\delta _{m}$ is the metalimnion thickness. Initially, the fluid is at rest. From the equation of state (EoS) of water, we can determine the density distribution, and the reduced gravity of the system, $g'\equiv (\Delta \rho /\rho _{0})g$, with $\Delta \rho$ the density difference between the deepest and the top layer, $\rho _{0}$ the reference density and $g$ the gravitational acceleration. The molecular properties of the fluid are the kinematic viscosity, $\nu$, and the thermal diffusivity, $\kappa$.

The nearshore basin is conceptually divided into two zones: a shallow plateau, zone (P), of length $\ell _{p}$, joined to a sloping bottom zone (S), of horizontal length $\ell _{s}$. Zone (S) extends until the point where the thermocline intersects the sloping bottom, and has a characteristic slope $\bar {s} \equiv (h_{m}-d)/\ell _{s}$, with $h'_{m}=h_{m}-d$. Farther offshore, the basin holds the interior stratified zone (I), of horizontal length longer than $\ell _{p}$ and $\ell _{s}$.

The surface boundary is subject to a uniform heat loss rate $H_{0}$, expressed as a kinematic heat flux $I_{0}=H_{0}/(\rho _{0}c_{p})$, with $c_{p}$ the specific heat capacity. The latter process cools surface waters. In turn, the heat loss leads to a positive and destabilising buoyancy flux $B_{0} =-g\alpha H_{0}/(\rho _{0}c_{p})$, with $\alpha =\rho ^{-1}_{0}(\partial \rho /\partial T)$ the thermal expansion coefficient, which forces natural convection. The velocity scale of the initial convective motions is well described by a balance between buoyancy and advection of kinetic energy, $w_{c}\simeq (B_{0}h'_{m})^{1/3}$ (Deardorff Reference Deardorff1970). Therefore, since convection will tend to locally homogenise the vertical temperature distribution, the depth-varying nearshore basin will experience differential cooling – the critical mechanism for driving thermal siphons.

2.2. Non-dimensional parameters and equations of motion

From the physical parameters introduced in § 2.1 $\{d,h'_{m},\ell _{p},\ell _{s},g',w_{c},\nu,\kappa \}$, we define six non-dimensional groups: three parameters associated with the flow dynamics,

(2.2a–c)\begin{equation} Pr\equiv \frac{\nu}{\kappa},\quad {Ri_{c}}\equiv\frac{g'h'_{m}}{w^{2}_{c}},\quad {Ra}\equiv \frac{w_{c}h'_{m}}{\kappa}, \end{equation}

and three parameters characterising the system's geometry,

(2.3a–c)\begin{equation} \bar{s}\equiv \frac{h'_{m}}{\ell_{s}},\quad A^{(v)}\equiv \frac{d}{h_{m}},\quad A^{(h)}\equiv\frac{\ell_{p}}{\ell_{s}}. \end{equation}

The first parameter in (2.2a–c) is the Prandtl number, here set to be $Pr=7$ to model thermally forced freshwater systems. The second parameter, the convective Richardson number $Ri_{c}$, compares the ratio of stabilising effects of the background stratification to the destabilising effects of convective stirring. The third parameter in (2.2a–c), the Rayleigh number $Ra$, establishes the scale separation between convective and diffusive heat transport.

The second parameter in (2.3a–c) describes the ratio between the shallow's depth and the mixing layer depth. We expect that as $A^{(v)}\rightarrow 0$, the difference between the cooling rate of the shallow and the cooling rate of the interior region becomes larger, thus speeding the formation of the thermal siphon. The third parameter, $A^{(h)}$, describes the ratio between the horizontal length-scales of zones (P) and (S). Thus, fixing $\ell _{s}$, one expects that smaller values of $A^{(h)}$ are associated with shorter time windows between the formation and the stabilisation of thermal siphons.

To expose the role of the non-dimensional numbers in the equations of motion, we scale the dimensional variables as follows: $x\sim \ell _{s}$, $z\sim h'_{m}$, $t\sim h'_{m}/w_{c}$, $\boldsymbol {v}\sim w_{c}$, $p/\rho _{0}\sim w^{2}_{c}$ and $\rho \sim \Delta \rho$. Defining the non-dimensional linear operators

(2.4a,b)\begin{equation} \tilde{{\boldsymbol{\nabla}}}_{\bar{s}}\equiv \bar{s} \left(\tilde{\partial}_{x}\,\hat{{\boldsymbol{i}}} + \tilde{\partial}_{y}\, \hat{{\boldsymbol{j}}}\right) + \tilde{\partial}_{z}\, \hat{{\boldsymbol{k}}} \quad \textrm{and} \quad \tilde{\nabla}^{2}_{\bar{s}}\equiv \tilde{{\boldsymbol{\nabla}}}_{\bar{s}} \boldsymbol{\cdot} \tilde{{\boldsymbol{\nabla}}}_{\bar{s}} = \bar{s}^{2} \left(\tilde{\partial}^{2}_{x} + \tilde{\partial}^{2}_{y}\right) + \tilde{\partial}^{2}_{z}, \end{equation}

the non-dimensional governing equations are given by

(2.5a)$$\begin{gather} (\tilde{\partial}_t + \tilde{\boldsymbol{v}}\boldsymbol{\cdot}{\tilde{\nabla}_{\bar{s}}}) \tilde{T} = {Ra}^{{-}1}\,{\tilde{\nabla}^{2}_{\bar{s}}}\,\tilde{T}, \end{gather}$$

(2.5b)$$\begin{gather}(\tilde{\partial}_t + \tilde{\boldsymbol{v}}\boldsymbol{\cdot}{\tilde{\nabla}_{\bar{s}}}) \tilde{\boldsymbol{v}} ={-}\tilde{\boldsymbol{\nabla}}_{\bar{s}}\,\tilde{p} - {Ri_{c}}\, \tilde{\rho}\,\hat{\boldsymbol{k}} + {Pr\, Ra}^{{-}1}{\tilde{\nabla}^{2}_{\bar{s}}}\, \tilde{\boldsymbol{v}}, \end{gather}$$

(2.5c)$$\begin{gather}{\tilde{\boldsymbol{\nabla}}_{\bar{s}}}\boldsymbol{\cdot}\tilde{\boldsymbol{v}} = 0, \end{gather}$$

where $\widetilde {(\boldsymbol {\cdot })}$ denotes non-dimensional variables. The non-dimensional parameters $\bar {s}$, $Pr$, $Ri_{c}$ and $Ra$ appear along with the various terms in (2.5). The latter provides insights into their role in the momentum and energy balances. The slope, $\bar {s}$, weights the importance of the horizontal advective acceleration and the horizontal pressure gradient. The convective Richardson number, $Ri_{c}$, weights the buoyancy term in the vertical momentum balance ($z$-axis). Moreover, the diffusion of momentum and heat are inversely proportional to the Rayleigh number, $({Pr\, Ra^{-1}})\tilde {\boldsymbol {\nabla }}^{2}_{\bar {s}}\tilde {\boldsymbol {v}}$ and $({Ra^{-1}})\tilde {\boldsymbol {\nabla }}^{2}_{\bar {s}}\tilde {T}$, respectively.

The scaling chosen in this study differs from the scaling adopted by Mao et al. (Reference Mao, Lei and Patterson2010). The Rayleigh numbers used by Mao et al. (Reference Mao, Lei and Patterson2010), here denoted as $Ra_h = B_{0} h'^{4}_{m} / \nu \kappa ^{2}$ and $Ra_g = B_{0} \ell ^{4}_{s} / \nu \kappa ^{2}$ (global Rayleigh number), result by considering velocity scales determined by a balance between the viscous term and the thermally driven pressure gradient. However, we can relate and compare the Rayleigh numbers in Mao et al. (Reference Mao, Lei and Patterson2010) with $Ra$ as $Ra_{h} = Ra^{3}\, Pr^{-1}$ and $Ra_{g} = Ra^{3}\, Pr^{-1}\,\bar {s}^{-4}$, respectively. In our study, $Ra$ will be substantially greater than the critical value for Rayleigh–Bénard convection on free-slip boundaries, $Ra^{c}_{h} \approx 657.5$ or $Ra^{c}\approx 16.6$. High-$Ra$ ensures a vigorous convective regime and that the diffusive terms in (2.5) play no critical role in the dynamic balances.

2.3. Convective regimes

Initially, the fluid ‘subject to a uniform surface cooling’ is found at rest, yet during a brief period. The time scale for the onset of thermal instabilities from the air–water interface can be estimated as $\tau _{B}\simeq \sqrt {657.5}\,\sqrt {\nu /B_{0}}$ (Bednarz et al. Reference Bednarz, Lei and Patterson2008). For typical values of $B_{0}$ in surface waterbodies (${\sim }10^{-10}\text {--}10^{-8}\ \textrm {W}\ \textrm {kg}^{-1}$), $\tau _{B}$ may vary from minutes to tens of minutes. Considering that the speed of the initial convective plumes scales as $w_{c}\simeq (B_{0}d)^{1/3}$ (${\sim }10^{-3}\ \textrm {m}\ \textrm {s}^{-1}$), with $d$ (${\sim }1\text {--}10\ \textrm {m}$) the vertical length-scale (Deardorff Reference Deardorff1970), the first thermals interacting with the bottom boundary have a travelling time of about $\tau _{RB}\simeq d/(dB_{0})^{1/3}$. Thus, the time scale $\tau _{RB}$ characterises the lifespan of the very initial convective regime, over which the system experiences RBTC without the influence of the sloping bottom boundary. The latter regime has a short duration, and its properties have been investigated by Bednarz et al. (Reference Bednarz, Lei and Patterson2008, Reference Bednarz, Lei and Patterson2009). In the present study we do not examine this initial convective regime. Instead, the study focuses on the convective dynamics occurring once thermals interact with the bottom physical boundaries until a LS-OC forms across the shallower sloping region – the thermal siphon.

Figure 2 depicts three convective regimes. In an early stage, RBTC dominates the fluid motion, characterised by local quasi-isotropic convective cells across the different zones, as illustrated in figure 2(a). Rayleigh–Bénard type convection supports, locally, the vertical homogenisation of the temperature in the surface layer. At the same time, the fluid builds up a cross-shore temperature gradient due to the differential cooling between shallow and deep waters, whereas convective cells start to grow gradually in the horizontal direction. We denote this first phase as regime I, and it takes place over a time window $\tau _{RB}< t\lesssim \tau _{t}$.

Figure 2. (a) Regime I characterises a system that hosts local, quasi-isotropic convective cells everywhere in the surface layer, while shallower waters become colder than deeper waters. This regime has a finite time window $\tau _{t}$ whose end characterises the transition to a flow dominated by horizontal convection. (b) Regime II is characterised by the expansion of horizontal convection, from the region that experiences the largest lateral temperature gradient, i.e. zone (S). During regime II, the left front of the growing horizontal convection cell propagates towards the lateral boundary at a speed $u_{f}$, as illustrated in panel (b). (c) Regime III starts when the front of the LS-OC occupies all zone (P), and a quasi-steady circulation is achieved, at a time $\tau _{qs}=\tau _{t} + \tau _{a}$.

After the ‘transition time scale’, $\tau _{t}$, the fluid motion is progressively dominated by horizontal density gradients. Thus, a LS-OC is expected to start from zone (S), which holds the largest cross-shore density gradient. We denote this second phase as regime II. Figure 2(b) schematises the expansion of the horizontal convective cell towards the shallowest lateral boundary due to a baroclinic adjustment. Its lateral growth occurs at a rate $u_{f}\equiv \textrm {d}\ell _{f}/\textrm {d} t$, with $\ell _{f}$ the position of the left front with respect to the position from where the expanding horizontal convection region emerges. Large-scale overturning circulation is characterised by a two-layer exchange flow, with a surface layer $h_{s}$ flowing toward the lateral boundary, whereas the bottom layer flows to the interior. Regime II takes place over a time scale $\tau _{a}$, which is the time required by the LS-OC to reach the lateral boundary, as illustrated in figure 2($c$). After a time scale $\tau _{qs} \simeq \tau _{t}+\tau _{a}$, we expect the LS-OC to achieve a quasi-steady state, denoted as regime III.

In what follows, we derive, in dimensional form, the dynamic regimes and time scales governing the transition from one regime to another.

2.3.1. Heat budgets in the absence of net horizontal transport

We look at the heat budget for each of the three zones shown in figure 2(a). Initially, convective motions are laterally localised and vertically confined due to the presence of a physical barrier, either the bottom boundary in zones (P) and (S) or the background stratification in zone (I). In flat zones (P) and (I), convective plumes diverge laterally without any particular horizontal preference. The latter is not the case in the sloping region, where we expect that part of the vertical momentum carried down by the thermals is transformed into horizontal momentum. However, since the slopes of natural systems are usually mild, $O(10^{-2})$, such a net transfer from vertical to horizontal momentum is rather weak. We will assume that during regime I, the net horizontal heat transport is negligible; thus, the heat balance can be approximated by

(2.6)\begin{equation} \partial_{t}T + \partial_{z}\left(wT\right) = \partial_{z}\left(\kappa\partial_{z}T\right), \end{equation}

where $\partial _{\xi }$ denotes the partial derivative with respect to an arbitrary variable $\xi$. We express the vertical average of a function $\varphi (t,z)$ over a layer $h$ as $\langle {\varphi }\rangle _{{(\boldsymbol {\cdot })}} = h^{-1}\int _{h}\varphi (t,z)\,\textrm {{d}}z$. Here, the subscript $(\boldsymbol {\cdot })$ will indicate zone (P), (S) or (I). Thus, integrating (2.6) over the water column $d$ in zone (P), and applying the boundary conditions of the problem, i.e. $w=0$ at $z=D-d$ and $z=D$, and $\kappa \partial _{z}T=-I_{0}$ at $z=D$ and $\kappa \partial _{z}T = 0$ at $z=D-d$, we obtain

(2.7)\begin{equation} \partial_{t}\langle T\rangle_{{(P)}} ={-}\frac{I_{0}}{d} . \end{equation}

Integrating (2.7) in time, and assuming that the initial time is $t_{0}=0$, the mean temperature in zone (P) evolves as

(2.8)\begin{equation} \langle T\rangle_{{(P)}} = \langle T(t_{0})\rangle_{{(P)}} -\frac{I_{0}}{d}t. \end{equation}

In zone (I), however, the heat budget integrates the contribution of the diffusive and advective fluxes at the base of the convective mixing layer,

(2.9)\begin{equation} \partial_{t}\langle T\rangle_{{(I)}} ={-}\frac{1}{h_{m }}\left\{I_{0}+(\kappa\partial_{z}T)\large|_{z=z_{m}} + ( w T)\large|_{z=z_{m}}\right\} , \end{equation}

where $z_{m}$ is the height at the base of the surface mixed layer. However, vertical fluxes at the base of the convective layer can be substantially diminished by the action of the temperature jump and the intensification of the background stratification (Deardorff, Willis & Lilly Reference Deardorff, Willis and Lilly1969; D'Asaro, Winters & Lien Reference D'Asaro, Winters and Lien2002). The net heat flux at a convective layer base is about one order of magnitude smaller than the surface heat flux (Zilitinkevich Reference Zilitinkevich1991). Therefore, in order to obtain an analytical approximation of $\langle T\rangle _{(I)}(t)$, the balance in (2.9) can be simplified to

(2.10)\begin{equation} \partial_{t}\langle T\rangle_{{(I)}} \approx{-}\frac{I_{0}}{h_{m }} , \end{equation}

thus,

(2.11)\begin{equation} \langle T\rangle_{{(I)}} \approx \langle T(t_{0})\rangle_{{(I)}} -\frac{I_{0}}{h_{m}}t . \end{equation}

In the sloping region (S) the $x$-dependent depth-averaged temperature evolution, $\langle T\rangle _{{(S)}}$, is analogous to (2.8) and (2.11) but normalised by the local depth, $D_{B}(x)$. Note that $\langle T(t_{0})\rangle _{{(P)}}=\langle T(t_{0})\rangle _{{(S)}}=\langle T(t_{0})\rangle _{{(I)}}$.

Since we are considering that $T>T_{MD}$, and that drops in temperature due to a cooling phase during a day are small relative to $T_{s}$ $({\sim }0.1^{\circ }\ \textrm {day}^{-1})$, a linear EoS provides a robust approximation to estimate the density, $\rho$, and buoyancy, $b$, for each zone, i.e.

(2.12)$$\begin{gather} \frac{\langle\rho\rangle_{{(\boldsymbol{\cdot})}}}{\rho_{0}}-1=\alpha\left(\langle T \rangle_{{(\boldsymbol{\cdot})}} - T_{0}\right) , \end{gather}$$

(2.13)$$\begin{gather}\langle b \rangle_{{(\boldsymbol{\cdot})}} ={-}g\left(\frac{\langle\rho\rangle_{{(\boldsymbol{\cdot})}}}{\rho_{0}}-1\right)={-} g\alpha\left(\langle T \rangle_{{(\boldsymbol{\cdot})}} - T_{0}\right) . \end{gather}$$

2.3.2. Vertical momentum balance

Now we consider the vertical momentum balance during the first regime,

(2.14)\begin{equation} \partial_{t}w + \boldsymbol{\nabla}\boldsymbol{\cdot}\left(\boldsymbol{v}w \right) ={-} \rho^{{-}1}_{0} \partial_{z}p + b + \nu\nabla^{2}w . \end{equation}

Assuming that natural convection controls the vertical momentum transport, i.e.that the advection of momentum balances buoyancy, the viscous term $\nu \nabla ^{2}w$ can be neglected from (2.14). As we show in § 2.2, (2.5b), the diffusion of momentum, $\nu \nabla ^{2}\boldsymbol {v}$, is inversely proportional to the Rayleigh number ($Ra$) of the system, thereby for high-$Ra$, the contribution of $\nu \nabla ^{2}\boldsymbol {v}$ becomes negligible. Therefore, averaging (2.14) between the surface $z=D$ and a height $z\geqslant D-d$, $\langle \boldsymbol {\cdot } \rangle _{{D-z}} = ({1}/({D -z}))\int ^{D}_{z} \boldsymbol {\cdot } \,\textrm {{d}}z$, and considering that variations of the vertical velocity during regime I are negligible, $\partial _{t}\langle w\rangle _{D-z}\sim 0$, the vertical momentum balance reduces to

(2.15)\begin{equation} \left.-\frac{w^{2}}{2}\right|_{z} \approx{-}\left(\frac{p_{{D}}-p}{\rho_{0}}\right) + \langle b \rangle_{{D-z}}\left(D-z\right) . \end{equation}

Here $p_{{D}}$ and $p$ denote the pressures at the surface and a height $z$, respectively. Then, the balance in (2.15), can be expressed as

(2.16)\begin{equation} \frac{p - p_{{D}}}{\rho_{0}} ={-} \langle b \rangle_{{D-z}}\left(D-z\right)-\left.\frac{w^{2}}{2}\right|_{z} . \end{equation}

The expression (2.16) shows that the pressure $p$ has a hydrostatic component, ${\langle b \rangle _{D-z}(D-z)}$, and a non-hydrostatic component, $w^{2}/2$.

2.3.3. Cross-shore pressure gradient

The cross-shore pressure gradient at $z=D-d$, the depth of zone (P), increases in time due to differential cooling. From (2.16) and (2.13), we can estimate $\partial _{x}p$ directly from the cross-shore temperature gradient,

(2.17)\begin{equation} \rho^{{-}1}_{0}\partial_{x} p = dg\alpha\partial_{x}\langle T \rangle_{{D-z}} . \end{equation}

A constant sloping bottom induces a uniform pressure gradient across zone (S). Thus, recalling that $B_{0}= -g\alpha I_{0}$, the time-dependent, cross-shore pressure gradient between zones (P) and (I) can be estimated from (2.8) and (2.11) as

(2.18)\begin{equation} \left.\rho^{{-}1}_{0}\partial_{x} p\right|_{z=D-d} \approx \frac{d g \alpha}{\ell_{s}}\left(\langle T \rangle_{{(I)}} - \langle T \rangle_{{(P)}}\right) ={-}\frac{B_{0}}{\ell_{s}}\left( 1 -\frac{d}{h_{m}}\right)t . \end{equation}

In general, the horizontal temperature difference, $\langle T\rangle _{{(I)}} - \langle T \rangle _{{(P)}}$, is substantially smaller than the temperature difference between the top and the bottom layer in the stratified interior region (I), $\Delta T$.

2.3.4. Cross-shore momentum balance

We examine now the cross-shore momentum balance during regime I,

(2.19)\begin{equation} \partial_{t}u + \boldsymbol{v}\boldsymbol{\cdot}\boldsymbol{\nabla}u ={-} \rho^{{-}1}_{0}\partial_{x}p + \nu\nabla^{2}u . \end{equation}

Previous works have considered a three-way linear momentum balance between the inertial, the viscous and the cross-shore pressure gradient terms to derive asymptotic solutions for the cross-shore velocity at small slopes and low-$Ra$ (Farrow & Patterson Reference Farrow and Patterson1993). Here, however, we use similar arguments to those adopted by Finnigan & Ivey (Reference Finnigan and Ivey1999) to integrate the role of advection, $\boldsymbol {v}\boldsymbol {\cdot }\boldsymbol {\nabla }u$, on the formation of a horizontal overturning due to an increase in time of the cross-shore pressure gradient. Neglecting the viscous term in (2.19), and considering that once the LS-OC starts the flow becomes largely horizontal, (2.19) reduces to the following three-way momentum balance:

(2.20)\begin{equation} \partial_{t}u + \partial_{x}\left(\frac{u^{2}}{2}\right) \approx{-} \partial_{x}\left(\frac{p}{\rho_{0}}\right) . \end{equation}

2.3.5. Transition time scale – $\tau _{t}$

We aim at determining the time scale at which the cross-shore pressure gradient balances the inertial terms in (2.20), i.e.

(2.21)\begin{equation} -\partial_{x}\left(\frac{p}{\rho_{0}}\right) \simeq \partial_{t}u\simeq \partial_{x}\left(\frac{u^{2}}{2}\right). \end{equation}

From (2.21) and the cross-shore pressure gradient in (2.18), we derive two horizontal velocity scales,

(2.22)$$\begin{gather} \partial_{t}u\simeq{-}\partial_{x}\left(\frac{p}{\rho_{0}}\right) \quad \rightarrow\quad u\simeq \frac{B_{0}}{\ell_{s}}\left( 1 -\frac{d}{h_{m}}\right)\frac{t^{2}}{2} , \end{gather}$$

(2.23)$$\begin{gather}\partial_{x}\left(\frac{u^{2}}{2}\right)\simeq{-}\partial_{x}\left(\frac{p}{\rho_{0}}\right) \quad \rightarrow\quad u\simeq \sqrt{2B_{0}\left( 1 -\frac{d}{h_{m}}\right)t} . \end{gather}$$

The three-way balance (2.21) is achieved at a time scale $\tau _{t}$ at which the velocity scale $u$ allows balancing the inertial terms with the cross-shore pressure gradient. Therefore, by equating expressions (2.22) and (2.23) yields

(2.24)\begin{equation} \tau_{t}\simeq \frac{2\ell_{s}}{\left(B_{0}\ell_{s}\right)^{1/3}}\left(1-\frac{d}{h_{m}}\right)^{{-}1/3} . \end{equation}

The time scale $\tau _{t}$ defines the transition from regime I to regime II, schematised in figure 2(b), and at $\tau _{t}$, the characteristic horizontal velocity scale, $u_{t}$, is given by

(2.25)\begin{equation} u_{t}\simeq 2\left(B_{0}\ell_{s}\right)^{1/3} \left(1-\frac{d}{h_{m}}\right)^{1/3} . \end{equation}

The exchange flow associated with the LS-OC should start developing in the zone with the maximum cross-shore pressure gradient, i.e. zone (S). Considering that this zone has a uniform slope, we expect the LS-OC to emerge at about the middle of zone (S), as shown later via numerical experiments.

2.3.6. Adjustment time scale – $\tau _{a}$

We now aim to determine the time scale required by the LS-OC to reach the lateral boundary in zone (P) and be adjusted to a new equilibrium state. This adjustment time scale, $\tau _{a}$, depends on the horizontal length of the nearshore area between the point from where the thermal siphon starts and the lateral boundary. During regime II, this nearshore area can be split into two regions, a region of length $\ell _{f}(t)$ (measured from the starting point) that grows in time due to the lateral expansion of the LS-OC and its neighbouring region that shrinks in time, where quasi-isotropic convective cells dominate the local flow, as depicted in figure 2(b). In this shrinking well-mixed zone, denoted as (LP), the average buoyancy results from the expressions (2.8) and (2.13),

(2.26)\begin{equation} \langle b \rangle_{{(LP)}} ={-}\frac{B_{0}}{d}\, t . \end{equation}

In zone (LP) the temperature and buoyancy are continuously decreasing, and $\langle b \rangle _{{(LP)}}$ matches the buoyancy at the left front of the horizontal convective cell, $\ell _{f}(t)$. Following the arguments by Phillips (Reference Phillips1966), we assume that the momentum of the surface layer current $u_{s}$ and buoyancy are found in an inertia–buoyancy balance. This assumption implies the flow within the horizontal convective cell scales as $u_{s}\simeq (2\langle b\rangle _{{(LP)}}h_{s}) ^{1/2}$, where $h_{s}$ is the thickness of the surface exchange layer, shown in figure 2(b). Additionally, we may also consider that the surface buoyancy flux, $B_{0}$, across $\ell _{f}$ is balanced with the production of kinetic energy, which leads to the scaling velocity $u_{s}\simeq (2B_{0}\ell _{f})^{1/3}$. Hence, the above two velocity scales are equal when

(2.27)\begin{equation} \langle b \rangle_{{(LP)}} \simeq \frac{\left(2B_{0}\ell_{f}\right)^{2/3}}{2h_{s}} . \end{equation}

By equating (2.26) and (2.27), we can derive the time scale required by the exchange flow to reach the lateral boundary. The latter is reached when $\ell _{f}(\tau _{a})\simeq \ell _{p}+\ell _{s}/2$,

(2.28)\begin{equation} \tau_{a} \simeq \frac{d}{h_{s}}\,\frac{\ell_{f}}{\left(2\ell_{f}B_{0}\right)^{1/3}} , \end{equation}

where $\tau _{a}$ represents the time scale needed for the LS-OC to fully adjust across zones (P) and (S). As a consequence, the time scale $\tau _{qs}\simeq \tau _{t}+\tau _{a}$ represents the time required to achieve the quasi-steady state that characterises regime III.

2.4. Numerical experiments

We examine the theoretical regimes derived in § 2.2 by means of numerical experiments. Previous studies investigated different forcing intensities for fixed basin's geometries (Horsch & Stefan Reference Horsch and Stefan1988; Bednarz et al. Reference Bednarz, Lei and Patterson2009; Mao et al. Reference Mao, Lei and Patterson2010). Here, instead, we vary the geometrical properties of the nearshore topography and keep the thermal forcing constant yet considering higher Rayleigh numbers than those examined in previous studies (Horsch & Stefan Reference Horsch and Stefan1988; Bednarz et al. Reference Bednarz, Lei and Patterson2009; Mao et al. Reference Mao, Lei and Patterson2010).

Building on the conceptual model and parameters introduced in §§ 2.1–2.2, we conducted four experiments listed in table 1. We considered three different slopes $\bar {s}$ below 10 %, which are representative of nearshore aquatic systems like lakes and coastal seas. Also, we examined two values for $A^{(h)}$ to test the impact of the plateau extent on the time scale $\tau _{qs}$. The initial stratification characterises a strongly stratified environment as observed in late summer in temperate lakes, with a convective Richardson number $Ri_{c}\approx 10^{3}$. Our numerical experiments explore moderate thermal forcing scenarios observed in natural aquatic systems, with Rayleigh numbers $Ra\approx 10^{5}$ and $Ra_{h}\approx 10^{5}$ introduced in § 2.2, and global Rayleigh numbers $10^{18}\leqslant Ra_{g}\leqslant 10^{20}$ defined by Mao et al. (Reference Mao, Lei and Patterson2010). Thus, the magnitude of the parameters adopted for the numerical experiments are close to those found in nearshore lakes (Bouffard & Wüest Reference Bouffard and Wüest2019, and references therein), and especially similar to those in Rotsee, Switzerland (Doda et al. Reference Doda, Ramón, Ulloa, Wüest and Bouffard2021). For the parameters used in the experiments, the time scales $\tau _{t}$ and $\tau _{qs}$, are shorter than $T_{day}=24$ h.

Table 1. Non-dimensional parameters of numerical experiments and time scales associated with the transition from regime I to regime II, $\tau _{t}$, and the transition from regime II to regime III, $\tau _{qs}$, with $T_{day}=24$ h. The ratios $\varDelta _{x,z}/(\eta _{K},\eta _{B})$ determine the global grid resolution in terms of the Kolmogorov and Batchelor scales, $\eta _{{K}}$ and $\eta _{{B}}$, respectively.

To achieve real-scale conditions, we resolved the two-dimensional version of the equations of motion (2.5) using a spectral large-eddy simulation (SLES) approach integrated in the solver flow_solve (Winters & de la Fuente Reference Winters and de la Fuente2012). The SLES approach combines a Laplacian operator with a high-order operator (‘hyper-diffusion’), which works on the temperature and the velocity fields to dissipate variance cascaded to the smallest scales near the grid spacing. This localised dissipation has a negligible effect at scales larger than a few times the grid resolution over a time scale of a few time steps (cf. Winters Reference Winters2016; Ulloa et al. Reference Ulloa, Winters, Wüest and Bouffard2020). A discussion of this approach and an explicit demonstration of the insensitivity to moderate changes in the parameters is given in Winters (Reference Winters2016). Table 1 compares the grid resolution of the numerical experiments, $\varDelta _{x}\approx \varDelta _{z}$, to the bulk Kolmogorov and Batchelor scales of the flow, $\eta _{K}$ and $\eta _{B}$, respectively (Appendix B), which were computed a posteriori. The simulations are characterised by $\varDelta _{x,z}/\eta _{K}<10$ and $\varDelta _{x,z}/\eta _{B}\leqslant 21$. For these spatial resolutions, Gayen, Griffiths & Hughes (Reference Gayen, Griffiths and Hughes2014) classified their numerical experiments as fairly resolved LES. Appendix A describes the numerical modelling approach, whereas tables 2 and 3 present the dimensional parameters used to set the numerical experiments.

Table 2. Numerical parameters kept invariant among the numerical experiments.

Table 3. Numerical parameters that vary among the numerical experiments.

3.1. Flow patterns and geometry

The results from the simulations show the existence of the three main convective regimes. As an example, we use exp. 1 (table 1) to illustrate the spatiotemporal flow patterns by examining the cross-shore velocity component, $u(t,\boldsymbol {x})$, and the streamfunction, $\psi (t,\boldsymbol {x})=\int ^{z}_{z_0} u(t,x,z)\, \textrm {d} z$, as shown in figure 3. Additionally, we examine the flow geometry, $F_{G}$, defined as

(3.1)\begin{equation} F_{G}(t) \equiv \frac{\sqrt{\langle u^{2}\rangle} +c}{\sqrt{\langle w^{2}\rangle}+c}. \end{equation}

The quantity $\langle \varphi \rangle$ denotes the spatial average of a function $\varphi$ over the plateau zone (P), whereas $c\ll \sqrt {\langle u^{2}\rangle }, \sqrt {\langle w^{2}\rangle }$ is a positive constant to avoid a singularity when fluid is at rest, i.e. before the onset of RBTC. Thus, $F_{G}$ is a positive defined function of time that provides information on the global geometry of the flow in the cross-shore/vertical plane, and we use it as a diagnostic parameter to identify the transition among the different regimes. When $F_{G}\approx 1$, the flow geometry is quasi-isotropic, and as $F_{G}$ turns larger than unity, the fluid trajectory becomes more elliptic, implying that on average, horizontal motions become more dominant than vertical motions.

Figure 3. Flow patterns described by the non-dimensional horizontal velocity component, $u/u_{t}$, and the non-dimensional streamfunction, $\tilde {\psi }=\psi /(u_{t}d)$, with $u_{t}$ the horizontal velocity scale defined in (2.25) at different non-dimensional times $t/\tau _{t}$, with $\tau _{t}$ the transition time scale in (2.24). (a,b) Instantaneous snapshot at $t/\tau _{t}=0.5$ for regime I. (c, d) Instantaneous snapshot at $t/\tau _{t}=1.5$ for regime II. (e, f) Instantaneous snapshot at $t/\tau _{t}=3.0$ for regime III. Values for $u_{t}$ and $\tau _{t}$ are provided in table 1. Movie 1 in the supplementary material available at https://doi.org/10.1017/jfm.2021.883 shows the spatiotemporal evolution of $u/u_{t}$ for exp. 1.

3.1.1. Regime I: $0< t/\tau _{t}<1$

Figure 3(a,b) shows the non-dimensional cross-shore velocity, $u/u_{t}$, along the non-dimensional streamfunction $\tilde {\psi } = \psi /(u_{t}d)$ on the plane $x$–$z$ at time $t/\tau _{t}=0.5$. Once convection begins, the flow pattern is organised in quasi-isotropic convective cells that occupy the whole water column in the plateau (P) and sloping (S) zones, and the mixed layer in the interior zone (I). The strength of convection is maximal in zone (I), and it decays towards the shallower zones (S) and (P), as shown in figure 3(a). In contrast, the stratified and deepest region in zone (I), $(D-z)/d>4.5$, exhibits weak but comparable flow magnitudes to those in zone (P), where convective plumes have the shortest vertical excursion, ${\sim }d$, making their convective speed the smallest one in the basin. In regime I, the fluid motion is extremely localised, and it is organised in an array of alternated clockwise and counter-clockwise circulation cells as shown by $\tilde {\psi }$ in figure 3(b).

Figure 4 shows the metric $F_{G}$, as a function of the non-dimensional time $t/\tau _{t}$, for each experiment. Initially, and by construction, $F_{G}=1$. At the onset of RBTC, $F_{G}$ exhibits momentarily values lower than unity since it integrates mostly vertical motion (see circle A). After this event, $F_{G}$ takes values partially higher than unity due to the quasi-isotropic characteristic of the convective flow, yet it shows a gradual increase until $t/\tau _{t}\approx 1$. At this time, $F_{G}$ reaches a value close to $1.5$.

Figure 4. Flow geometry, $F_{G}$, as a function of the non-dimensional time $t/\tau _{t}$. Values for $\tau _{t}$ are summarised in table 1. Circle A denotes the onset of RBTC. Circle B stresses the time for the transition to horizontal convection. Circle C highlights the instants when the horizontal convective cell reaches the lateral boundary, $x/\ell _{s}=0$.

3.1.2. Regime II: $1\lesssim t/\tau _{t}<\tau _{qs}/\tau _{t}$

Regime II exhibits a progressive change in the flow pattern. Figure 3(c,d) shows $u/u_{\tau }$ and $\tilde {\psi }$, respectively, at time $t/\tau _{t}=1.5$. The transition from quasi-isotropic convective cells to a LS-OC occurs at about $t/\tau _{t}\approx 1$, when convective cells start to merge and organise in a greater elliptical cell near the upper half of the sloping zone (S), $1\leqslant x/\ell _{s}\leqslant 1.5$. Figure 3(d) shows the signature of such a process, where we identify a large counterclockwise circulation taking place across the boundary between zones (P) and (S). This circulation pattern has a distinctive two-layer exchange flow, with a bottom layer running downslope from zone (P) to zone (S) and a surface layer flowing in the reverse direction.

The structure of the exchange flow that propagates upslope is well defined, with a depth for the stagnation point stable in time. As the left front of the LS-OC propagates across zone (P), it erodes the region that is still dominated by quasi-isotropic convective cells. On the other hand, the structure of the exchange flow that propagates downslope is rather chaotic and pulsating, and its signature becomes weaker as it reaches zone (I). At the same time, an equally large but less coherent clockwise circulation is formed across zones (S) and (I), $1.75\leqslant x/\ell _{s}\leqslant 2.25$, whereas further offshore, the flow pattern is governed by RBTC, as shown in figure 3(c,d) for $2.5\leqslant x/\ell _{s}\leqslant 3.5$.

The metric $F_{G}$ shows a break in its trend at $t/\tau _{t}\approx 1$, as shown on the highlighted circle B in figure 4. We associate this break with the expansion of horizontal convection that characterises regime II. Indeed, $F_{G}$ experiences a remarkable increase in its growth rate due to the shift from quasi-isotropic convective cells to the LS-OC that occurs across zones (S) and (P). As time progresses, however, $F_{G}$ starts to reduce its growth ($t/\tau _{t}>2$) in a way that the curves begin to converge and oscillate around a value of $F_{G}\approx 5$, indicating that fluid motion in zone (P) is predominantly horizontal.

From the results in figure 4, the time associated with the shift from regime II to regime III is not evident. However, circle C highlights a marked change in $F_{G}$ that allows identifying the emergence of a new dynamic regime. We found that the oscillatory signal that starts at $t/\tau _{t}\approx 1.8$ for exp. 4 occurs when the left front of the LS-OC reaches the lateral boundary, $x/\ell _{s}=0$. After this time, $F_{G}(t)$ oscillates around $F_{G}\approx 5$. To estimate the time scale associated with the transition from regime II to regime III, $\tau _{qs}\simeq \tau _{t}+\tau _{a}$, we require the thickness of the surface exchange layer $h_{s}$, depicted in figure 2(b), which is so far unknown. However, both $\tau _{qs}$ and $h_{s}$ can be obtained from the numerical experiments.

We first estimate the time $\tau ^{(exp)}_{qs}$ at which the left front reaches the lateral boundary $x/\ell _{s}=0$. For this, we look at the evolution of the near-surface, cross-shore velocity, defined by convenience as

(3.2)\begin{equation} \bar{u}_{s}(t,x)\equiv \frac{1}{d/3}\int^{D}_{D-d/3} u(t,x,z) \, \textrm{d}z . \end{equation}

Knowing that the upper layer velocity of the LS-OC has a negative sign and propagates towards the shore ($x/\ell _{s}=0$), its left front is easy to track by examining $\bar {u}_{s}$.

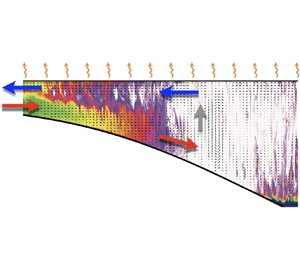
Figure 5 shows $\bar {u}_{s}(t,x)/u_{t}$ (colour map) for each experiment. The horizontal axes denote the non-dimensional position $x/\ell _{s}$ whereas the vertical axes denote the non-dimensional time $t/\tau _{t}$. Blue colours denote on-shore currents, while red colours denote off-shore currents. Thus, the evolution of the blue region is associated with the irreversible expansion of the LS-OC that starts approximately about $t/\tau _{t}\simeq 1$, in the middle of zone (S). In particular, the left diagonal boundary of the large blue region denotes the spatiotemporal position of the front, and its intersection with the vertical axis at $x/\ell _{s}=0$ (marked by a green circle) allows for estimating $\tau ^{(exp)}_{qs}$.

Figure 5. Near-surface cross-shore velocity, $\bar {u}_{s}(t,x)$, normalised by $u_{t}$ as a function of cross-shore position $x/\ell _{s}$ and time $t/\tau _{t}$ for (a) exp. 1, (b) exp. 2, (c) exp. 4 and (d) exp. 3 (see table 1). Note that exp. 1 and exp. 4 have been placed one on top of the other for easier visual comparison. Each map is divided in nine regions. Across the space coordinate $x/\ell _{s}$, we distinguish: the plateau zone (P), between $x/\ell _{s}=0$ and the left vertical dashed line; the sloping zone (S), between the two vertical dashed lines; and the interior zone (I), between the right vertical dashed line and $x/\ell _{s}=3.5$. On the time coordinate $t/\tau _{t}$, we identify: the theoretical regime I, $0< t/\tau _{t}\lesssim 1$, followed by the regime II, between $t/\tau _{t}\simeq 1$ and the time when the left front of the exchange flow reaches $x/\ell _{s}=0.0$, marked by a green circle on the vertical axis. This time is denoted as $\tau ^{(exp)}_{qs}$. Regime III is characterised by times $t/\tau _{t}$ above the upper horizontal dashed line.

The empirical estimation of $\tau _{qs}$ allows for examining the adjustment time scale $\tau _{a}$ (2.28), which depends on the characteristic thickness of the upper exchange layer, $h_{s}$. Figure 3(e) provides a spatial view of $u/u_{t}$, and shows that $h_{s}$ varies little across zone (P). In figure 6 we provide a detailed view of the cross-shore velocity profile $u/u_{t}$ at the middle of zone (P). Green lines in figure 6 show the time-averaged velocity profile over regime I, $\bar {u}_{{R1}}/u_{t}$. Its maximum magnitude, $\bar {u}_{{R1}}/u_{t}\sim O(0.1)$, and vertical distribution results from time averaging a flow dominated by localised, quasi-isotropic convective cells. Red lines show the time-averaged velocity profile over regime II, $\bar {u}_{{R2}}/u_{t}$. To obtain $\bar {u}_{{R2}}/u_{t}$, we followed two steps. We first used $\tau ^{(exp)}_{qs}$ (estimated from figure 5) to examine the vertical structure of the time-averaged velocity profile over $t\in [\tau _{t},\tau ^{(exp)}_{qs}]$. From this velocity profile, we found that $h^{(exp)}_{s}/d\approx 0.35$ for all the experiments. We then used the experimental value of $h^{({\rm exp})}_{s}$ to re-estimate $\tau _{a}$ and $\tau _{qs}\simeq \tau _{t}+\tau _{a}(h^{(exp)}_{s})$ from the theoretical expressions (2.24) and (2.28). Thus, $\bar {u}_{{R2}}/u_{t}$ in figure 6 results from a time averaging over $t\in [\tau _{t},\tau _{qs}(h^{(exp)}_{s})]$. We use then $\tau _{qs}$ to normalise the evolution in time of $F_{G}$, as shown in figure 7. In this new non-dimensional time, all the curves of $F_{G}$ collapse after $t/\tau _{qs}=1$, which defines the end of regime II and the beginning of regime III.

Figure 6. Non-dimensional cross-shore velocity component, $u/u_{t}$, at the middle point $x_{*}$ of zone (P). (a) Exp. 1, $x/\ell _{s}=0.5$. (b) Exp. 2, $x/\ell _{s}=0.5$. (c) Exp. 3, $x/\ell _{s}=0.5$. (d) Exp. 4, $x/\ell _{s}=0.25$. Note that exp. 1 and exp. 4 have been placed one on top of the other for easier visual comparison. Grey lines show the superimposed velocity profiles of $u$ over the three regimes. Green lines show the time-averaged velocity profile, $\bar {u}_{{R1}}$, over regime I. Red lines show the time-averaged velocity profile, $\bar {u}_{{R2}}$, over regime II. Blue lines show the time-averaged velocity profile, $\bar {u}_{{R3}}$, over regime III. The horizontal dashed line denotes $(D-z)/d = 0.35$.

Figure 7. Flow geometry, $F_{G}$, as a function of the non-dimensional time $t/\tau _{qs}$. Values for $\tau _{qs}$ are summarised in table 1.

3.2. Cross-shore transport

The development of the LS-OC boosts the cross-shore transport, $\mathcal {Q}_{{Exp}}$. Here, we quantify $\mathcal {Q}_{{Exp}}(t)$ at the boundary between zones (P) and (S), where a two-layer exchange flow is well defined,

(3.3)\begin{equation} \mathcal{Q}_{{Exp}}(t) \equiv \tfrac{1}{2}\int^{D}_{D-d} |u(t,x=\ell_{p},z)|\, \textrm{d}z . \end{equation}

In the quasi-steady state the cross-shore transport can be estimated from Phillips (Reference Phillips1966) velocity scale, $(B_{0}\ell _{p})^{1/3}$, and the local depth, $d$, as

(3.4)\begin{equation} \mathcal{Q}_{qs}\simeq \mathcal{A} d\left(B_{0}\ell_{p}\right)^{1/3} , \end{equation}

where $\mathcal {A}$ is a constant coefficient to be determined. For the conditions in regime III, we compute for each experiment $\mathcal {Q}_{{Exp}}(t)$ and the respective time-averaged coefficient $\mathcal {A}$,

(3.5)\begin{equation} \bar{\mathcal{A}}_{{Exp}} = \frac{1}{d \left(B_{0}\ell_{p}\right)^{1/3}}\left\{ \frac{1}{\tau_{m}-\tau_{qs}}\int^{\tau_{m}}_{\tau_{qs}} Q_{{Exp}}(t) \, \textrm{d} t\right\}. \end{equation}

Figure 8 shows the time series of $\mathcal {Q}_{{Exp}}(t)$ for each experiment, normalised by their respective scaling $\mathcal {Q}_{qs}$, with $\bar {\mathcal {A}}=(1/4)\sum ^{4}_{i=1}\bar {\mathcal {A}}_{{Exp\,i}}=0.35 \pm 0.05$. The time-averaged values $\bar {\mathcal {A}}_{{Exp\,i}}$, along with their standard deviations, are summarised in the legend of figure 8. The time axis in figure 8 is normalised by $\tau _{qs}$, which allows stressing the transition between regimes II to III at $t/\tau _{qs}\simeq 1$. In this non-dimensional time, the time series of $\mathcal {Q}_{{Exp}}(t)/\mathcal {Q}_{qs}$ show a first transient phase over which the magnitude of the cross-shore transport has significant variability as well as a progressive increase. Not surprisingly, $\mathcal {Q}_{{Exp}}(t)/\mathcal {Q}_{qs}$ shows a stabilisation before $t/\tau _{qs}=1$. The latter is due to the fact that at the location where we measure $Q_{{Exp}}(t)$, the horizontal exchange flow forms earlier than the time $\tau _{qs}$ required to reach the lateral boundary. For times $t/\tau _{qs}\geqslant 1$, the results show a quasi-steady cross-shore transport, with a standard deviation $\sigma$ of about $15\,\%$ over its mean value. Thus, for the set of parameters considered in the numerical experiments, the scaling $\mathcal {Q}_{qs}\simeq 0.35d(B_{0}\ell _{p})^{1/3}$ is a robust predictor of the cross-shore transport between zones (P) and (S) under quasi-steady-state conditions.

Figure 8. Experimental cross-shore transport $\mathcal {Q}_{{Exp}}(t)$ scaled by $\mathcal {Q}_{qs}=\bar {\mathcal {A}}\,d(B_{0} \ell _{p})^{1/3}$, with $\bar {\mathcal {A}}=0.35\pm 0.05$.

3.3. Evolution of the cross-shore thermal field

Figure 9 shows the spatiotemporal evolution of the non-dimensional temperature field $(T-T_{b})/\Delta T$ for exp. 1. Zone (P) has the coolest temperature above the thermocline height, whereas the convective mixing layer in zone (I) is the warmest region.

Figure 9. Spatiotemporal evolution of the relative temperature field $(T-T_{b})/\Delta T$. Zone (P): $0\leqslant x/\ell _{s}\leqslant 1$; zone (S): $1\leqslant x/\ell _{s}\leqslant 2$; zone (I): $2\leqslant x/\ell _{s}\leqslant 3.5$. Movie 2 in the supplementary material shows the spatiotemporal evolution of $(T-T_{b})/\Delta T$ for exp. 1.

During regime I ($0\leqslant t/\tau _{t}< 1.0$), waters above the thermocline remain vertically well mixed due to turbulent convection. Zones (P) and (I) also remain horizontally mixed. As time progresses, a cross-shore temperature difference builds up between zones (P) and (I), where the maximum horizontal temperature gradient is found across zone (S) ($1.0\leqslant x/\ell _{s}\leqslant 2.0$), as shown in figure 9(a). However, we identify that at about $t/\tau _{t}\simeq 1.0$ warmer waters entrain above colder waters in zone (P) ($x/\ell _{s}\approx 1.5$), as shown in figure 9(b). This localised overturn is associated with the development of the overturning circulation that characterise regime II.

Figure 9(c–e) shows the thermal structure resulting from the growing LS-OC during regime II. In this phase we observe the formation of a layer of cold water flowing downslope from the upper region of zone (S). At the same time, a surface layer formed by warmer waters coming from zone (S) penetrates across zone (P). Once the LS-OC is fully developed across zone (P), i.e. when regime III starts, the water column exhibits an almost uniform temperature profile towards the lateral boundary, $x/ \ell _{s}\rightarrow 0$, and towards the end of zone (S), $x/\ell _{s} \simeq 2.0$, as shown in figure 9( f). Within this region, the exchange flow keeps waters weakly stratified and feeds a gravity current that propagates downslope. Yet, as the gravity current crosses zone (S) and approaches zone (I), its signature becomes substantially weaker and intermittent while convective plumes get more vigorous, enhancing vertical mixing and supporting the degeneration of the exchange flow. In the previous subsections we used the velocity field properties to show that the formation of the LS-OC agrees well with the transition time scale, $\tau _{t}$, in (2.24). However, for practical reasons, one might wish to infer the conditions that support forming a thermal siphon in an aquatic system by measuring the temperature at specific locations. Theoretically, the dynamic balance that controls the formation of the thermal siphon (§ 2.3.4) has a specific cross-shore temperature gradient to fulfil. In our framework, expressions (2.8) and (2.11) allow for determining the mean temperature difference and thermal gradient between zones (P) and (I) at the transition time scale $t=\tau _{t}$,

(3.6a)$$\begin{gather} \varDelta\langle T\rangle_{{(IP)}} = \langle T\rangle_{{(I)}} - \langle T\rangle_{{(P)}} \approx \frac{I_{0}}{d}\left(1 - \frac{d}{h_{m}}\right)\tau_{t} , \end{gather}$$

(3.6b)$$\begin{gather}\partial _{x}\langle T\rangle_{{(IP)}} = \frac{\langle T\rangle_{{(I)}} - \langle T\rangle_{{(P)}}}{\ell_{s}} \approx \frac{I_{0}}{d \ell_{s}}\left(1 - \frac{d}{h_{m}}\right)\tau_{t} , \end{gather}$$

respectively. Both expressions depend only on the geometrical properties of the nearshore basin and the kinematic heat flux $I_{0}$. Therefore, they can be readily used to determine the mean temperature difference between the shallow and interior waters, or the mean cross-shore temperature gradient, that supports the formation of a LS-OC in a waterbody.

Note that $\langle T\rangle _{{(P)}}$ is higher than the temperature of the deeper layer, $T_{b}$, which means that the lower branch of LS-OC can not plunge into the deeper layer of the interior basin.

We tested the ability of expression (3.6a) to predict the temperature difference between shallow and interior waters at $\tau _{t}$. For this, we computed times series of $\varDelta \langle T\rangle _{{(IP)}}(t)$, and we scaled them by their respective temperature difference predicted in (3.6a). Figure 10 shows $[\varDelta \langle T\rangle _{{(IP)}}(t)]_{exp}/\varDelta \langle T\rangle _{{(IP)}}(\tau _{t})$ as a function of the non-dimensional time $t/\tau _{t}$. The dashed line bisecting the map represents the theoretical linear trend expected during regime I ($0 < t/\tau _{t}<1$). Thus, for a perfect agreement, the curves should cross the coordinate (1,1). Indeed, the experimental temperature difference $[\varDelta \langle T\rangle _{{(IP)}}]_{exp}$ at $\tau _{t}$ shows values of about 90 % of the theoretically predicted.

Figure 10. Relative temperature difference between the shallow and interior waters as a function of time. Capital letters (A), (B) and (C) are associated with capital letters in figure 11.

Recalling the hypotheses adopted to derive (3.6a), i.e.no horizontal heat exchange and that the mean temperature in zone (I) is dominated by the surface heat flux, our numerical results show that these assumptions are met reasonably well, and the level of disagreement is expected. Figure 11(a) shows a close-up view of the temperature field overlapped by the velocity field in zone (S) for exp. 1 at $t/\tau _{t}=1$. The temperature field is still almost vertically mixed, and the flow field is organised in localised convective cells, suggesting that no exchange between zones (P) and (I) takes place yet.

Figure 11. Relative temperature field $(T-T_{b})/\Delta T$ within zone (S), $1\leqslant x/\ell _{s}\leqslant 2$, superposed by the velocity field (black arrows) for (a) $t/\tau _{t}=1.0$, (b) $t/\tau _{t}=1.3$ and (c) $t/\tau _{t}=3.0$. Capital letters (A), (B) and (C) are associated with capital letters in figure 10.

For $t/\tau _{t}>1$, nonetheless, the curves $[\varDelta \langle T\rangle _{{(IP)}}(t)]_{exp}/\varDelta \langle T\rangle _{{(IP)}}(\tau _{t})$ start departing progressively from the dashed line due to the horizontal heat exchange that takes place across zone (S). Thus, the analytical expression (3.6a) grants a conservative estimation of the temperature difference between shallow and interior waters required to drive the LS-OC across the sloping region. However, to generate an effective heat exchange between zone (P) and the interior zone (I), the fluid within each extreme zone must first be transported all through zone (S). Therefore, we anticipate that the collapse of the curves should hold until the heat exchange driven by the LS-OC starts to influence the mean temperatures in zones (P) and (I). Indeed, we observe in figure 10 that this horizontal heat exchange becomes distinctive at about $t/\tau _{t} \gtrsim 1.3$. As an example, figure 11(b) illustrates that in exp. 1 at $t/\tau _{t}=1.3$, the heat exchange is already occurring between zones (P) and (S). After the above experimental time, the curves $[\varDelta \langle T\rangle _{{(IP)}}(t)]_{exp}/\varDelta \langle T\rangle _{{(IP)}}(\tau _{t})$ start to depart from each other and the non-dimensional temperature difference between (P) and (I) starts to grow at a slower rate due to the horizontal heat exchange throughout zone (S), as shown in figure 11(c).