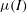Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-26T08:39:57.677Z Has data issue: false hasContentIssue false
  • English
  • Français

A depth-averaged $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mu (I)$-rheology for shallow granular free-surface flows

Published online by Cambridge University Press:  20 August 2014

J. M. N. T. Gray  and
A. N. Edwards
J. M. N. T. Gray*
Affiliation:
School of Mathematics and Manchester Centre for Nonlinear Dynamics, University of Manchester, Manchester M13 9PL, UK
A. N. Edwards
Affiliation:
School of Mathematics and Manchester Centre for Nonlinear Dynamics, University of Manchester, Manchester M13 9PL, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The 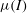$\mu (I)$-rheology is a nonlinear viscous law, with a strain-rate invariant and pressure-dependent viscosity, that has proved to be effective at modelling dry granular flows in the intermediate range of the inertial number, 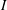$I$. This paper shows how to incorporate the rheology into depth-averaged granular avalanche models. To leading order, the rheology generates an effective basal friction, which is equivalent to a rough bed friction law. A depth-averaged viscous-like term can be derived by integrating the in-plane deviatoric stress through the avalanche depth, using pressure and velocity profiles from a steady-uniform solution to the full 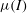$\mu (I)$-rheology. The resulting viscosity is proportional to the thickness to the three halves power, with a coefficient of proportionality that is angle dependent. When substituted into the depth-averaged momentum balance this term generates second-order derivatives of the depth-averaged velocity, which are multiplied by a small parameter. Its inclusion therefore represents a singular perturbation to the equations. It is shown that a granular front propagating down a rough inclined plane is completely unaffected by the rheology, but, discontinuities, which naturally develop in inviscid roll-wave solutions, are smoothed out. By comparison with existing experimental data, it is shown that the depth-averaged 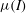$\mu (I)$-rheology accurately predicts the growth rate of spatial instabilities to steady-uniform flow, as well as the dependence of the cutoff frequency on the Froude number and inclination angle. This provides strong evidence that, in the steady-uniform flow regime, the predicted decrease in the viscosity with increasing slope is correct. Outside the range of angles where steady-uniform flows develop, the viscosity becomes negative, which implies that the equations are ill-posed. This is a signature of the ill-posedness of the full 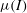$\mu (I)$-rheology at both high and low inertial numbers. The depth-averaged 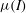$\mu (I)$-rheology therefore cannot be used outside the valid range of angles without additional regularization.

JFM classification

Granular media: Granular media Non-Newtonian Flows: Rheology Waves/Free-surface Flows: Surface gravity waves
Type
Papers
Information
Journal of Fluid Mechanics , Volume 755 , 25 September 2014 , pp. 503 - 534
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramowitz, M. & Stegun, I. 1970 Handbook of Mathematical Functions, 9th edn. p. 3.3.7. Dover.Google Scholar
Ancey, C., Coussot, P. & Evesque, P. 1999 A theoretical framework for granular suspensions in a steady simple shear flow. J. Rheol. 43 (6), 1673–1699.CrossRefGoogle Scholar
Barbolini, M., Domaas, U., Faug, T., Gauer, P., Hákonardóttir, K. M., Harbitz, C. B., Issler, D., Jóhannesson, T., Lied, K., Naaim, M., Naaim-Bouvet, F. & Rammer, L.2009 EUR 23339 – the design of avalanche protection dams – recent practical and theoretical developments. European Commission.Google Scholar
Barker, T., Schaeffer, D. G., Bohórquez, P. & Gray, J. M. N. T. 2014 Well-posed and ill-posed behaviour of the $\mu ({I})$ -rheology for granular flow. J. Fluid Mech. (submitted).Google Scholar
Bouchut, F. & Westdickenberg, M. 2004 Gravity driven shallow water models for arbitrary topography. Commun. Math. Sci. 2, 359–389.CrossRefGoogle Scholar
Christen, M., Kowalski, J. & Bartelt, P. 2010 Ramms: numerical simulation of dense snow avalanches in three-dimensional terrain. Cold Reg. Sci. Technol. 63, 1–14.CrossRefGoogle Scholar
Cui, X. & Gray, J. M. N. T. 2013 Gravity-driven granular free-surface flow around a circular cylinder. J. Fluid Mech. 720, 314–337.CrossRefGoogle Scholar
Cui, X., Gray, J. M. N. T. & Jóhannesson, T. 2007 Deflecting dams and the formation of oblique shocks in snow avalanches at Flateyri, Iceland. J. Geophys. Res. 112, F04012.Google Scholar
Denlinger, R. P. & Iverson, R. M. 2001 Flow of variably fluidized granular masses across three-dimensional terrain: 2. Numerical predictions and experimental tests. J. Geophys. Res. 106 (B1), 553–566.CrossRefGoogle Scholar
Doyle, E. E., Hogg, A. J. & Mader, H. 2011 A two-layer approach to modelling the transformation of dilute pyroclastic currents into dense pyroclastic flows. Proc. R. Soc. A 467 (2129), 1348–1371.CrossRefGoogle Scholar
Fischer, J. T., Kowalski, J. & Pudasaini, S. 2012 Topographic curvature effects in applied avalanche modeling. Cold Reg. Sci. Technol. 74–75, 21–30.CrossRefGoogle Scholar
Forterre, Y. 2006 Kapiza waves as a test for three-dimensional granular flow rheology. J. Fluid Mech. 563, 123–132.CrossRefGoogle Scholar
Forterre, Y. & Pouliquen, O. 2003 Long-surface-wave instability dense granular flows. J. Fluid Mech. 486, 21–50.Google Scholar
GDR-MiDi, 2004 On dense granular flows. Eur. Phys. J. E 14, 341–365.CrossRefGoogle Scholar
Goldhirsch, I. 2003 Rapid granular flows. Annu. Rev. Fluid Mech. 35 (1), 267–293.CrossRefGoogle Scholar
Gray, J. M. N. T. & Ancey, C. 2009 Segregation, recirculation and deposition of coarse particles near two-dimensional avalanche fronts. J. Fluid Mech. 629, 387–423.CrossRefGoogle Scholar
Gray, J. M. N. T. & Cui, X. 2007 Weak, strong and detached oblique shocks in gravity driven granular free-surface flows. J. Fluid Mech. 579, 113–136.CrossRefGoogle Scholar
Gray, J. M. N. T. & Kokelaar, B. P. 2010a Large particle segregation, transport and accumulation in granular free-surface flows. J. Fluid Mech. 652, 105–137.CrossRefGoogle Scholar
Gray, J. M. N. T. & Kokelaar, B. P. 2010b Large particle segregation, transport and accumulation in granular free-surface flows—erratum. J. Fluid Mech. 657, 539.CrossRefGoogle Scholar
Gray, J. M. N. T., Tai, Y. C. & Noelle, S. 2003 Shock waves, dead-zones and particle-free regions in rapid granular free-surface flows. J. Fluid Mech. 491, 161–181.CrossRefGoogle Scholar
Gray, J. M. N. T., Wieland, M. & Hutter, K. 1999 Free surface flow of cohesionless granular avalanches over complex basal topography. Proc. R. Soc. A 455, 1841–1874.CrossRefGoogle Scholar
Greve, R. & Hutter, K. 1993 Motion of a granular avalanche in a convex and concave curved chute: experiments and theoretical predictions. Phil. Trans. R. Soc. Lond. A 342, 573–600.Google Scholar
Grigorian, S. S., Eglit, M. E. & Iakimov, I. L. 1967 New state and solution of the problem of the motion of snow avalance. Snow, Avalanches & Glaciers. Tr. Vysokogornogo Geofizich Inst. 12, 104–113.Google Scholar
Hákonardóttir, K. M. & Hogg, A. J. 2005 Oblique shocks in rapid granular flows. Phys. Fluids 17, 0077101.CrossRefGoogle Scholar
Iverson, R. M. 1997 The physics of debris-flows. Rev. Geophys. 35, 245–296.CrossRefGoogle Scholar
Iverson, R. M. & Denlinger, R. P. 2001 Flow of variably fluidized granular masses across three-dimensional terrain 1. Coulomb mixture theory. J. Geophys. Res. 106 (B1), 553–566.Google Scholar
Jenkins, J. T. & Savage, S. B. 1983 A theory for the rapid flow of identical, smooth, nearly elastic, spherical-particles. J. Fluid Mech. 130, 187–202.CrossRefGoogle Scholar
Johnson, C. G. & Gray, J. M. N. T. 2011 Granular jets and hydraulic jumps on an inclined plane. J. Fluid Mech. 675, 87–116.CrossRefGoogle Scholar
Jop, P., Forterre, Y. & Pouliquen, O. 2005 Crucial role of sidewalls in granular surface flows: consequences for the rheology. J. Fluid Mech. 541, 167–192.CrossRefGoogle Scholar
Jop, P., Forterre, Y. & Pouliquen, O. 2006 A constitutive relation for dense granular flows. Nature 44, 727–730.CrossRefGoogle Scholar
Jordan, D. W. & Smith, P. 1987 Nonlinear Ordinary Differential Equations. Oxford University Press.Google Scholar
Kuo, C., Tai, Y. C., Bouchut, F., Mangeney, A., Pelanti, M., Chen, R. & Chang, K. 2009 Simulation of Tsaoling landslide, Taiwan, based on Saint Venant equations over general topography. Engng Geol. 104 (3–4), 181–189.CrossRefGoogle Scholar
Lagrée, P.-Y., Staron, L. & Popinet, S. 2011 The granular column collapse as a continuum: validity of a two-dimensional Navier–Stokes model with a $\mu (I)$ -rheology. J. Fluid Mech. 686, 378–408.CrossRefGoogle Scholar
Luca, I., Hutter, K., Tai, Y. C. & Kuo, C. Y. 2009 A hierarchy of avalanche models on arbitrary topography. Acta Mechanica 205, 121–149.CrossRefGoogle Scholar
Majmudar, T. S. & Behringer, R. P. 2005 Contact force measurements and stress-induced anisotropy in granular materials. Nature 435, 1079–1082.CrossRefGoogle ScholarPubMed
Mangeney, A., Bouchut, F., Thomas, N., Vilotte, J. P. & Bristeau, M. O. 2007 Numerical modeling of self-channeling granular flows and of their levee-channel deposits. J. Geophys. Res. 112, F02017.Google Scholar
Mangeney, A., Roche, O., Hungr, O., Mangold, N., Faccanoni, G. & Lucas, A. 2010 Erosion and mobility in granular collapse over sloping beds. J. Geophys. Res. 115, F03040.Google Scholar
Mangeney-Castelnau, A., Vilotte, J. P., Bristeau, M. O., Perthame, B., Bouchut, F., Simeoni, C. & Yerneni, S. 2003 Numerical modeling of avalanches based on Saint-Venant equations using a kinetic scheme. J. Geophys. Res. 108, 2527–2544.Google Scholar
Needham, D. J. & Merkin, J. H. 1984 On roll waves down an open inclined channel. Proc. R. Soc. 394, 259–278.Google Scholar
Pitman, E. B., Nichita, C. C., Patra, A., Bauer, A., Sheridan, M. & Bursik, M. 2003 Computing granular avalanches and landslides. Phys. Fluids 15 (12), 3638–3646.CrossRefGoogle Scholar
Pouliquen, O. 1999a Scaling laws in granular flows down rough inclined planes. Phys. Fluids 11 (3), 542–548.CrossRefGoogle Scholar
Pouliquen, O. 1999b On the shape of granular fronts down rough inclined planes. Phys. Fluids 11 (7), 1956–1958.CrossRefGoogle Scholar
Pouliquen, O., Delour, J. & Savage, S. B. 1997 Fingering in granular flows. Nature 386, 816–817.CrossRefGoogle Scholar
Pouliquen, O. & Forterre, Y. 2002 Friction law for dense granular flows: application to the motion of a mass down a rough inclined plane. J. Fluid Mech. 453, 133–151.CrossRefGoogle Scholar
Pouliquen, O. & Vallance, J. W. 1999 Segregation induced instabilities of granular fronts. Chaos 9 (3), 621–630.CrossRefGoogle ScholarPubMed
Pudasaini, S. P. & Hutter, K. 2003 Rapid shear flows of dry granular masses down curved and twisted channels. J. Fluid Mech. 495, 193–208.CrossRefGoogle Scholar
Razis, D., Edwards, A. N., Gray, J. M. N. T. & van der Weele, K. 2014 Arrested coarsening of granular roll waves. Phys. Fluids (submitted).CrossRefGoogle Scholar
Sampl, P. & Zwinger, T. 2004 Avalanche simulation with SAMOS. Ann. Glaciol. 38 (1), 393–398.CrossRefGoogle Scholar
Savage, S. B. 1984 The mechanics of rapid granular flows. Adv. Appl. Mech. 24, 289–366.CrossRefGoogle Scholar
Savage, S. B. & Hutter, K. 1989 The motion of a finite mass of granular material down a rough incline. J. Fluid Mech. 199, 177–215.CrossRefGoogle Scholar
Savage, S. B. & Hutter, K. 1991 The dynamics of avalanches of granular materials from initiation to run-out. I. Analysis. Acta Mechanica 86, 201–223.CrossRefGoogle Scholar
Sovilla, B., Schaer, M., Kern, M. & Bartelt, P. 2008 Impact pressures and flow regimes in dense snow avalanches observed at the Vallée de la Sionne test site. J. Geophys. Res. 113, F01010.Google Scholar
Staron, L., Lagrée, P.-Y. & Popinet, S. 2012 The granular silo as a continuum plastic flow: the hour-glass vs the clepsydra. Phys. Fluids 24, 103301.CrossRefGoogle Scholar
Strogatz, S. H. 1994 Nonlinear Dynamics and Chaos. Westview Press.Google Scholar
Tai, Y. C., Noelle, S., Gray, J. M. N. T. & Hutter, K. 2002 Shock-capturing and front-tracking methods for granular avalanches. J. Comput. Phys. 175, 269–301.CrossRefGoogle Scholar
Vreman, A. W., Al-Tarazi, M., Kuipers, J. A. M., Sint, M. V. & Bokhove, O. 2007 Supercritical shallow granular flow through a contraction: experiment, theory and simulation. J. Fluid Mech. 578, 233–269.CrossRefGoogle Scholar
Wieland, M., Gray, J. M. N. T. & Hutter, K. 1999 Channelised free surface flow of cohesionless granular avalanches in a chute with shallow lateral curvature. J. Fluid Mech. 392, 73–100.CrossRefGoogle Scholar
Woodhouse, M. J., Thornton, A. R., Johnson, C. G., Kokelaar, B. P. & Gray, J. M. N. T. 2012 Segregation-induced fingering instabilities in granular free-surface flows. J. Fluid Mech. 709, 543–580.CrossRefGoogle Scholar
Wu, W., Bauer, E. & Kolymbas, D. 1996 Hypoplastic constitutive model with critical state for granular materials. Mech. Mater. 23 (1), 45–69.CrossRefGoogle Scholar