Published online by Cambridge University Press: 07 December 2015
Using two-dimensional direct numerical simulations, we investigate the flow in a fluid of kinematic viscosity  ${\it\nu}$ and density
${\it\nu}$ and density 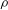 ${\it\rho}$ around elliptical foils of density
${\it\rho}$ around elliptical foils of density 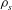 ${\it\rho}_{s}$ with major axis
${\it\rho}_{s}$ with major axis  $c$ and minor axis
$c$ and minor axis 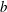 $b$ for three different aspect ratios:
$b$ for three different aspect ratios: 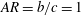 $AR=b/c=1$ (a circle);
$AR=b/c=1$ (a circle); 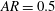 $AR=0.5$; and
$AR=0.5$; and 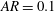 $AR=0.1$. The vertical location of these foils
$AR=0.1$. The vertical location of these foils 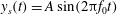 $y_{s}(t)=A\sin (2{\rm\pi}f_{0}t)$ oscillates with amplitude
$y_{s}(t)=A\sin (2{\rm\pi}f_{0}t)$ oscillates with amplitude 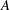 $A$ and frequency
$A$ and frequency 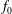 $f_{0}$ in two distinct ways: ‘pure’ oscillation, where the foils are constrained to remain in place; and ‘flying’ oscillation, where horizontal motion is allowed. We simulate the flow for a range of the two appropriate control parameters, the non-dimensional amplitude, or Keulegan–Carpenter number
$f_{0}$ in two distinct ways: ‘pure’ oscillation, where the foils are constrained to remain in place; and ‘flying’ oscillation, where horizontal motion is allowed. We simulate the flow for a range of the two appropriate control parameters, the non-dimensional amplitude, or Keulegan–Carpenter number 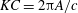 $KC=2{\rm\pi}A/c$, and the non-dimensional frequency, or Stokes number
$KC=2{\rm\pi}A/c$, and the non-dimensional frequency, or Stokes number 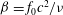 ${\it\beta}=f_{0}c^{2}/{\it\nu}$. We observe three distinct patterns of asymmetry, labelled ‘S-type’ for synchronous asymmetry, ‘
${\it\beta}=f_{0}c^{2}/{\it\nu}$. We observe three distinct patterns of asymmetry, labelled ‘S-type’ for synchronous asymmetry, ‘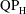 $\text{QP}_{\text{H}}$-type’ and ‘
$\text{QP}_{\text{H}}$-type’ and ‘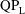 $\text{QP}_{\text{L}}$-type’ for quasi-periodic asymmetry at sufficiently high and sufficiently low (i.e.
$\text{QP}_{\text{L}}$-type’ for quasi-periodic asymmetry at sufficiently high and sufficiently low (i.e. 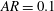 $AR=0.1$) aspect ratios, respectively. These patterns are separated at the critical locus in
$AR=0.1$) aspect ratios, respectively. These patterns are separated at the critical locus in 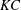 $KC$–
$KC$–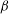 ${\it\beta}$ space by a ‘freezing point’ where the two incommensurate frequencies of the QP-type flows combine, and we show that this freezing point tends to occur at smaller values of
${\it\beta}$ space by a ‘freezing point’ where the two incommensurate frequencies of the QP-type flows combine, and we show that this freezing point tends to occur at smaller values of 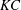 $KC$ as
$KC$ as 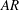 $AR$ decreases. We find for the smallest aspect ratio case (
$AR$ decreases. We find for the smallest aspect ratio case (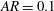 $AR=0.1$) that the transition to asymmetry, for all values of
$AR=0.1$) that the transition to asymmetry, for all values of 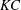 $KC$, occurs for a critical value of an ‘amplitude’ Stokes number
$KC$, occurs for a critical value of an ‘amplitude’ Stokes number 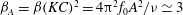 ${\it\beta}_{A}={\it\beta}(KC)^{2}=4{\rm\pi}^{2}f_{0}A^{2}/{\it\nu}\simeq 3$. The
${\it\beta}_{A}={\it\beta}(KC)^{2}=4{\rm\pi}^{2}f_{0}A^{2}/{\it\nu}\simeq 3$. The 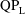 $\text{QP}_{\text{L}}$-type asymmetry for
$\text{QP}_{\text{L}}$-type asymmetry for 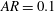 $AR=0.1$ is qualitatively different in physical and mathematical structure from the
$AR=0.1$ is qualitatively different in physical and mathematical structure from the 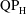 $\text{QP}_{\text{H}}$-type asymmetry at higher aspect ratio. The flows at the two ends of the ellipse become essentially decoupled from each other for the
$\text{QP}_{\text{H}}$-type asymmetry at higher aspect ratio. The flows at the two ends of the ellipse become essentially decoupled from each other for the 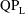 $\text{QP}_{\text{L}}$-type asymmetry, the two frequencies in the horizontal force signature being close to the primary frequency, rather than twice the primary frequency as in the
$\text{QP}_{\text{L}}$-type asymmetry, the two frequencies in the horizontal force signature being close to the primary frequency, rather than twice the primary frequency as in the 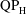 $\text{QP}_{\text{H}}$-type asymmetry. Furthermore, the associated coefficients arising from a Floquet stability analysis close to the critical thresholds are profoundly different for low aspect ratio foils. Freedom to move slightly suppresses the transition to S-type asymmetry, and for certain parameters, if a purely oscillating foil subject to S-type asymmetry is released to move, flow symmetry is rapidly recovered due to the negative feedback of small horizontal foil motion. Conversely, for the ‘higher’ aspect ratios, the transition to
$\text{QP}_{\text{H}}$-type asymmetry. Furthermore, the associated coefficients arising from a Floquet stability analysis close to the critical thresholds are profoundly different for low aspect ratio foils. Freedom to move slightly suppresses the transition to S-type asymmetry, and for certain parameters, if a purely oscillating foil subject to S-type asymmetry is released to move, flow symmetry is rapidly recovered due to the negative feedback of small horizontal foil motion. Conversely, for the ‘higher’ aspect ratios, the transition to 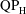 $\text{QP}_{\text{H}}$-type asymmetry is encouraged when the foil is allowed to move, with strong positive feedback occurring between the shed vortices from successive oscillation cycles. For
$\text{QP}_{\text{H}}$-type asymmetry is encouraged when the foil is allowed to move, with strong positive feedback occurring between the shed vortices from successive oscillation cycles. For 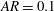 $AR=0.1$, freedom to move significantly encourages the onset of asymmetry, but the newly observed ‘primary’
$AR=0.1$, freedom to move significantly encourages the onset of asymmetry, but the newly observed ‘primary’ 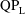 $\text{QP}_{\text{L}}$-type asymmetry found for pure oscillation no longer occurs when the foil flies, with S-type asymmetry leading ultimately to locomotion at a constant speed occurring all along the transition boundary for all values of
$\text{QP}_{\text{L}}$-type asymmetry found for pure oscillation no longer occurs when the foil flies, with S-type asymmetry leading ultimately to locomotion at a constant speed occurring all along the transition boundary for all values of 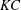 $KC$ and
$KC$ and 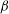 ${\it\beta}$.
${\it\beta}$.