Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-28T22:09:05.544Z Has data issue: false hasContentIssue false
  • English
  • Français

Density ratio effects on reacting bluff-body flow field characteristics

Published online by Cambridge University Press:  11 July 2012

Benjamin Emerson ,
Jacqueline O’Connor ,
Matthew Juniper  and
Tim Lieuwen
Benjamin Emerson*
Affiliation:
Georgia Institute of Technology, School of Aerospace Engineering, 270 Ferst Dr, Atlanta, GA 30332, USA
Jacqueline O’Connor
Affiliation:
Georgia Institute of Technology, School of Aerospace Engineering, 270 Ferst Dr, Atlanta, GA 30332, USA
Matthew Juniper
Affiliation:
Cambridge University Engineering Department, Trumpington Street, Cambridge CB2 1PZ, UK
Tim Lieuwen
Affiliation:
Georgia Institute of Technology, School of Aerospace Engineering, 270 Ferst Dr, Atlanta, GA 30332, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The wake characteristics of bluff-body-stabilized flames are a strong function of the density ratio across the flame and the relative offset between the flame and shear layer. This paper describes systematic experimental measurements and stability calculations of the dependence of the flow field characteristics and flame sheet dynamics upon flame density ratio, , over the Reynolds number range of 1000–3300. We show that two fundamentally different flame/flow behaviours are observed at high and low 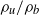values: a stable, noise-driven fixed point and limit-cycle oscillations, respectively. These results are interpreted as a transition from convective to global instability and are captured well by stability calculations that used the measured velocity and density profiles as inputs. However, in this high-Reynolds-number flow, the measurements show that no abrupt bifurcation in flow/flame behaviour occurs at a given 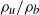value. Rather, the flow field is highly intermittent in a transitional 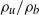range, with the relative fraction of the two different flow/flame behaviours monotonically varying with 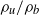. This intermittent behaviour is a result of parametric excitation of the global mode growth rate in the vicinity of a supercritical Hopf bifurcation. It is shown that this parametric excitation is due to random fluctuations in relative locations of the flame and shear layer.

JFM classification

Instability: Absolute/convective instability Reacting Flows: Combustion Wakes/Jets: Wakes
Type
Papers
Information
Journal of Fluid Mechanics , Volume 706 , 10 September 2012 , pp. 219 - 250
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Present address: Sandia National Laboratories, Engine Combustion Department, PO Box 969 MS 9053, Livermore, CA 94551-0969, USA.

References

1. Anderson, K. R., Hertzberg, J. & Mahalingam, S. 1996 Classification of absolute and convective instabilities in premixed bluff body stabilized flames. Combust. Sci. Technol. 112 (1), 257–269.CrossRefGoogle Scholar
2. Anselmo-Filho, P., Hochgreb, S., Barlow, R. S. & Cant, R. S. 2009 Experimental measurements of geometric properties of turbulent stratified flames. Proc. Combust. Inst. 32, 1763–1770.CrossRefGoogle Scholar
3. Aquaro, D. & Pieve, M. 2007 High temperature heat exchangers for power plants: performance of advanced metallic recuperators. Appl. Therm. Engng 27 (2–3), 389–400.CrossRefGoogle Scholar
4. Baudoin, E., Yu, R., Nogenmyr, K. J., Bai, X. S. & Fureby, C. 2009 Comparison of LES models applied to a bluff body stabilized flame. In 47th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL. AIAA. AIAA-2009-1178.Google Scholar
5. Bearman, P. 1969 On vortex shedding from a circular cylinder in the critical Reynolds number regime. J. Fluid Mech. 37 (3), 577–585.CrossRefGoogle Scholar
6. Beer, J. & Chigier, N. 1972 Combustion Aerodynamics. John Wiley and Sons.Google Scholar
7. Bers, A. 1983 Handbook of Plasma Physics I: Basic Plasma Physics. North-Holland.Google Scholar
8. Bill, R. G. Jr. & Tarabanis, K. 1986 The effect of premixed combustion on the recirculation zone of circular cylinders. Combust. Sci. Technol. 47, 39–53.CrossRefGoogle Scholar
9. Blevins, R. D. 1977 Flow-Induced Vibration. Van Nostrand Reinhold Co.Google Scholar
10. Briggs, R. J. 1964 Electron-stream Interaction with Plasmas. MIT.CrossRefGoogle Scholar
11. Cantwell, B. & Coles, D. 1983 An experimental study of entrainment and transport in the turbulent near wake of a circular cylinder. J. Fluid Mech. 136, 321–374.CrossRefGoogle Scholar
12. Cardell, G. S. 1993 Flow past a circular cylinder with a permeable wake splitter plate. PhD thesis, California Insititute of Technology, Pasadena.Google Scholar
13. Chaudhuri, S. & Cetegen, B. M. 2009 Response dynamics of bluff-body stabilized conical premixed turbulent flames with spatial mixture gradients. Combust. Flame 156 (3), 706–720.CrossRefGoogle Scholar
14. Chaudhuri, S., Kostka, S., Renfro, M. W. & Cetegen, B. M. 2010 Blowoff dynamics of bluff body stabilized turbulent premixed flames. Combust. Flame 157 (4), 790–802.CrossRefGoogle Scholar
15. Criminale, W. O., Jackson, T. L. & Joslin, R. D. 2003 Theory and Computation in Hydrodynamic Stability. Cambridge University Press.CrossRefGoogle Scholar
16. Cross, C., Fricker, A., Shcherbik, D., Lubarsky, E., Zinn, B. T. & Lovett, J. A. 2010 Dynamics of non-premixed bluff body-stabilized flames in heated air flow. In ASME Turbo Expo, Glasgow, UK. GT2010-23059.Google Scholar
17. Crump, J. E., Schadow, K. C., Yang, V. & Culick, F. E. C. 1986 Longitudinal combustion instabilities in Ramjet engines: identification of acoustic modes. J. Propul. Power 2 (2), 105–109.CrossRefGoogle Scholar
18. Erickson, R. R. & Soteriou, M. C. 2011 The influence of reactant temperature on the dynamics of bluff body stabilized premixed flames. Combust. Flame 158 (12), 2441–2457.CrossRefGoogle Scholar
19. Hertzberg, J. R., Shepherd, I. G. & Talbot, L. 1991 Vortex shedding behind rod stabilized flames. Combust. Flame 86, 1–11.CrossRefGoogle Scholar
20. Hilborn, R. C. 1994 Chaos and Nonlinear Dynamics. Oxford University Press.Google Scholar
21. Ho, C.-M. & Huerre, P. 1984 Perturbed Free Shear Layers. University of Southern California.CrossRefGoogle Scholar
22. Horsthemke, W. & Lefever, R. 1984 Noise Induced Transitions. Springer.Google Scholar
23. Huang, R. F. & Chang, K. T. 2004 Oscillation frequency in wake of a vee gutter. J. Propul. Power 20 (5), 871–878.CrossRefGoogle Scholar
24. Huerre, P. & Monkewitz, P. A. 1985 Absolute and convective instabilities in free shear layers. J. Fluid Mech. 159, 151–168.CrossRefGoogle Scholar
25. Huerre, P. & Monkewitz, P. A. 1990 Local and global instabilities in spatially developing flows. Annu. Rev. Fluid Mech. 22 (1), 473–537.CrossRefGoogle Scholar
26. Juniper, M. P., Tammisola, O. & Lundell, F. 2011 The local and global stability of confined planar wakes at intermediate Reynolds number. J. Fluid Mech. 686, 218–238.CrossRefGoogle Scholar
27. Karlovitz, B., Denniston, D. W., Knapschaefer, D. H. & Wells, F. E. 1953 Studies on turbulent flames. Proc. Combust. Inst. 4, 613–620.CrossRefGoogle Scholar
28. Kholmyansky, M., Moriconi, L. & Tsinober, A. 2007 Large-scale intermittency in the atmospheric boundary layer. Phys. Rev. E 76 (2).CrossRefGoogle ScholarPubMed
29. Kiel, B., Garwick, K., Lynch, A., Gord, J. R. & Meyer, T. 2006 Non-reacting and combusting flow investigation of bluff bodies in cross flow. In 42nd AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Sacramento, California. AIAA-2006-5234.Google Scholar
30. Kiel, B., Garwick, K., Lynch, A. & Gord, A. 2007 A detailed investigation of bluff body stabilized flames. In 45th AIAA Aerospace Sciences Meeting & Exhibit, Reno, Nevada. AIAA-2007-168.Google Scholar
31. Kim, K. T. & Hochgreb, S. 2011 The nonlinear heat release response of stratified lean-premixed flames to acoustic velocity oscillations. Combust. Flame 158, 2482–2499.CrossRefGoogle Scholar
32. Kim, W., Lienau, J., van Slooten, P., Colket, M., Malecki, R. & Syed, S. 2006 Towards modelling lean blowout in gas turbine flameholder applications. Trans. ASME: J. Engng Gas Turbines Power 128, 40–48.Google Scholar
33. Kolmogorov, A. N. 1962 A refinement of previous hypotheses concerning the local structure of turbulence in a viscous incompressible fluid at high Reynolds number. J. Fluid Mech. 13 (1), 82–85.CrossRefGoogle Scholar
34. Lieuwen, T. C. & Yang, V. (ed.) 2005 Combustion instabilities in gas turbine engines: operational experience, fundamental mechanisms, and modeling. Prog. Astronaut. Aeronaut. 210.Google Scholar
35. Lovett, J. A., Brogan, T. P., Philippona, D. S., Keil, B. V. & Thompson, T. V. 2004 Development needs for advanced afterburner designs. 40th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Fort Lauderdale, FL. AIAA-2004-4192.Google Scholar
36. Masselin, M. & Ho, C.-M. 1985 Lock-on and instability in a flat plate wake. In AIAA Shear Flow Control Conference, Boulder, CO. AIAA-1985-571.Google Scholar
37. Mei, R. 1996 Velocity fidelity of flow tracer particles. Exp. Fluids 22, 1–13.CrossRefGoogle Scholar
38. Melling, A. 1997 Tracer particles and seeding for particle image velocimetry. Meas. Sci. Technol. 8, 1406–1416.CrossRefGoogle Scholar
39. Monkewitz, P. A. 1988 The absolute and convective nature of instability in two-dimensional wakes at low Reynolds numbers. Phys. Fluids 31 (5).CrossRefGoogle Scholar
40. Nair, S. 2006 Acoustic detection of blowout phenomenon. PhD thesis, Georgia Institute of Technology, Atlanta, GA.Google Scholar
41. Nair, S. & Lieuwen, T. 2005 Acoustic detection of blowout in premixed flames. J. Propul. Power 21, 32–39.CrossRefGoogle Scholar
42. Nichols, J. W., Schmid, P. J. & Riley, J. J. 2007 Self-sustained oscillations in variable-density round jets. J. Fluid Mech. 582, 341–376.CrossRefGoogle Scholar
43. Pan, J. C., Vangsness, M. D. & Ballal, D. R. 1992 Aerodynamics of bluff-body stabilized confined turbulent premixed flames. Trans. ASME: J. Engng Gas Turbines Power 114, 783–789.Google Scholar
44. Perry, A. E., Chong, M. S. & Lim, T. T. 1982 The vortex shedding process behind two-dimensional bluff bodies. J. Fluid Mech. 116, 77–90.CrossRefGoogle Scholar
45. Poinsot, T. J., Trouve, A. C., Veynante, D. P., Candel, S. M. & Esposito, E. J. 1987 Vortex-driven acoustically coupled combustion instabilities. J. Fluid Mech. 177, 265–292.CrossRefGoogle Scholar
46. Pomeau, Y. & Manneville, P. 1980 Intermittent transition to turbulence in dissipative dynamical systems. Commun. Math. Phys. 74, 189–197.CrossRefGoogle Scholar
47. Potter, A. E. Jr. & Wong, E. L. 1958 Effect of pressure and duct geometry on bluff-body flame stabilization. National Advisory Committee on Aeronautics, Cleveland, OH.Google Scholar
48. Prasad, A. & Williamson, C. H. K. 1997 The instability of the shear layer separating from a bluff body. J. Fluid Mech. 333, 375–402.CrossRefGoogle Scholar
49. Rai, M. M. 2010 A computational investigation of the instability of the detached shear layers in the wake of a circular cylinder. J. Fluid Mech. 659, 375–404.CrossRefGoogle Scholar
50. Rao, K. N., Narasimha, R. & Badri Narayanan, M. A. 1971 The ‘bursting’ phenomenon in a turbulent boundary layer. J. Fluid Mech. 48 (2), 339–352.CrossRefGoogle Scholar
51. Rees, S. J. 2009 Hydrodynamic instability of confined jets & wakes and implications for gas turbine fuel injectors. PhD thesis, University of Cambridge.Google Scholar
52. Rees, S. J. & Juniper, M. 2010 The effect of confinement on the stability of viscous planar jets and wakes. J. Fluid Mech. 656, 309–336.CrossRefGoogle Scholar
53. Roshko, A. 1954 On the drag and shedding frequency of two-dimensional bluff bodies. National Advisory Committee on Aeronautics.Google Scholar
54. Roshko, A. 1955 On the wake and drag of bluff bodies. J. Aeronaut. Sci. 22 (2), 124–132.CrossRefGoogle Scholar
55. Roshko, A. 1961 Experiments on the flow past a cylinder at very high Reynolds numbers. J. Fluid Mech. 10, 345–356.CrossRefGoogle Scholar
56. Schlichting, H. & Gersten, K. 2000 Boundary-Layer Theory. Springer.CrossRefGoogle Scholar
57. Schmid, P. J. & Henningson, D. S. 2001 Stability and Transition in Shear Flows. Springer.CrossRefGoogle Scholar
58. Shanbhogue, S. 2008 Dynamics of perturbed exothermic bluff-body flow-fields. PhD thesis, School of Aerospace Engineering, Georgia Institute of Technology, Atlanta, GA.Google Scholar
59. Shanbhogue, S. J., Husain, S. & Lieuwen, T. 2009a Lean blowoff of bluff body stabilized flames: scaling and dynamics. Prog. Energy Combust. Sci. 35 (1), 98–120.CrossRefGoogle Scholar
60. Shanbhogue, S. J., Shin, D.-H., Hemchandra, S., Plaks, D. & Lieuwen, T. 2009b Flame-sheet dynamics of bluff-body stabilized flames during longitudinal acoustic forcing. Proc. Combust. Inst. 32 (2), 1787–1794.CrossRefGoogle Scholar
61. Smith, D. A. & Zukoski, E. E. 1985 Combustion instability sustained by unsteady vortex combustion. In AIAA/SAE/ASME/ASEE Joint Propulsion Conference, Monterey, CA. AIAA-1985-1248.Google Scholar
62. Soteriou, M. C. & Ghoniem, A. F. 1994 The vorticity dynamics of an exothermic, spatially developing, forced reacting shear layer. Proc. Combust. Inst. 25 (1), 1265–1272.CrossRefGoogle Scholar
63. Thurston, D. W. 1958 An experimental investigation of flame spreading from bluff body flameholders. Engineer’s thesis, California Institute of Technology, Pasadena.Google Scholar
64. Waugh, I. C. & Juniper, M. P. 2011 Triggering in a thermoacoustic system with stochastic noise. Int. J. Spray Combust. Dyn. 3 (3), 225–242.CrossRefGoogle Scholar
65. White, F. M. 2006 Viscous Fluid Flow. McGraw-Hill.Google Scholar
66. Williams, F. A. 1966 Flame stabilization of premixed turbulent gases. Appl. Mech. Surveys 1157–1170.Google Scholar
67. Yamaguchi, S., Ohiwa, N. & Hasegawa, T. 1985 Structure and blow-off mechanism of rod-stabilized premixed flame. Combust. Flame 62, 31–41.CrossRefGoogle Scholar
68. Yang, J. T., Yen, C. W. & Tsai, G. L. 1994 Flame stabilization in the wake flow behind a slit v-gutter. Combust. Flame 99, 288–294.CrossRefGoogle Scholar
69. Yang, V. & Culick, F. E. C. 1986 Analysis of low frequency combustion instabilities in a laboratory Ramjet combustor. Combust. Sci. Technol. 45, 1–25.CrossRefGoogle Scholar
70. Yu, M.-H. & Monkewitz, P. A. 1990 The effect of non-uniform density on the absolute instability of two-dimensional inertial jets and wakes. Phys. Fluids A 2 (7), 1175–1181.CrossRefGoogle Scholar
71. Zdravkovich, M. M. 1997 Flow Around Circular Cylinders: A Comprehensive Guide Through Flow Phenomena, Experiments, Applications, Mathematical Models, and Computer Simulations. Oxford University Press.CrossRefGoogle Scholar