Article contents
Degeneration of internal Kelvin waves in a continuous two-layer stratification
Published online by Cambridge University Press: 15 July 2015
Abstract
We explore the evolution of the gravest internal Kelvin wave in a two-layer rotating cylindrical basin, using direct numerical simulations (DNS) with a hyper-viscosity/diffusion approach to illustrate different dynamic and energetic regimes. The initial condition is derived from Csanady’s (J. Geophys. Res., vol. 72, 1967, pp. 4151–4162) conceptual model, which is adapted by allowing molecular diffusion to smooth the discontinuous idealized solution over a transition scale,  ${\it\delta}_{i}$, taken to be small compared to both layer thicknesses
${\it\delta}_{i}$, taken to be small compared to both layer thicknesses 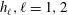 $h_{\ell },\ell =1,2$. The different regimes are obtained by varying the initial wave amplitude,
$h_{\ell },\ell =1,2$. The different regimes are obtained by varying the initial wave amplitude, 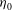 ${\it\eta}_{0}$, for the same stratification and rotation. Increasing
${\it\eta}_{0}$, for the same stratification and rotation. Increasing 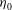 ${\it\eta}_{0}$ increases both the tendency for wave steepening and the shear in the vicinity of the density interface. We present results across several regimes: from the damped, linear–laminar regime (DLR), for which
${\it\eta}_{0}$ increases both the tendency for wave steepening and the shear in the vicinity of the density interface. We present results across several regimes: from the damped, linear–laminar regime (DLR), for which 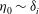 ${\it\eta}_{0}\sim {\it\delta}_{i}$ and the Kelvin wave retains its linear character, to the nonlinear–turbulent transition regime (TR), for which the amplitude
${\it\eta}_{0}\sim {\it\delta}_{i}$ and the Kelvin wave retains its linear character, to the nonlinear–turbulent transition regime (TR), for which the amplitude 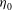 ${\it\eta}_{0}$ approaches the thickness of the (thinner) upper layer
${\it\eta}_{0}$ approaches the thickness of the (thinner) upper layer 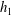 $h_{1}$, and nonlinearity and dispersion become significant, leading to hydrodynamic instabilities at the interface. In the TR, localized turbulent patches are produced by Kelvin wave breaking, i.e. shear and convective instabilities that occur at the front and tail of energetic waves within an internal Rossby radius of deformation from the boundary. The mixing and dissipation associated with the patches are characterized in terms of dimensionless turbulence intensity parameters that quantify the locally elevated dissipation rates of kinetic energy and buoyancy variance.
$h_{1}$, and nonlinearity and dispersion become significant, leading to hydrodynamic instabilities at the interface. In the TR, localized turbulent patches are produced by Kelvin wave breaking, i.e. shear and convective instabilities that occur at the front and tail of energetic waves within an internal Rossby radius of deformation from the boundary. The mixing and dissipation associated with the patches are characterized in terms of dimensionless turbulence intensity parameters that quantify the locally elevated dissipation rates of kinetic energy and buoyancy variance.
- Type
- Papers
- Information
- Copyright
- © 2015 Cambridge University Press
References
- 16
- Cited by



