Published online by Cambridge University Press: 28 March 2019
We present a dynamic decomposition analysis of the wake flow in fluid–structure interaction (FSI) systems under both laminar and turbulent flow conditions. Of particular interest is to provide the significance of low-dimensional wake flow features and their interaction dynamics to sustain the free vibration of a square cylinder at a relatively low mass ratio. To obtain the high-dimensional data, we employ a body-conforming variational FSI solver based on the recently developed partitioned iterative scheme and the dynamic subgrid-scale turbulence model for a moderate Reynolds number (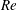 $Re$). The snapshot data from high-dimensional FSI simulations are projected to a low-dimensional subspace using the proper orthogonal decomposition (POD). We utilize each corresponding POD mode to detect features of the organized motions, namely, the vortex street, the shear layer and the near-wake bubble. We find that the vortex shedding modes contribute solely to the lift force, while the near-wake and shear layer modes play a dominant role in the drag force. We further examine the fundamental mechanism of this dynamical behaviour and propose a force decomposition technique via low-dimensional approximation. To elucidate the frequency lock-in, we systematically analyse the decomposed modes and their dynamical contributions to the force fluctuations for a range of reduced velocity at low Reynolds number laminar flow. These quantitative mode energy contributions demonstrate that the shear layer feeds the vorticity flux to the wake vortices and the near-wake bubble during the wake–body synchronization. Based on the decomposition of wake dynamics, we suggest an interaction cycle for the frequency lock-in during the wake–body interaction, which provides the interrelationship between the high-amplitude motion and the dominating wake features. Through our investigation of wake–body synchronization below critical
$Re$). The snapshot data from high-dimensional FSI simulations are projected to a low-dimensional subspace using the proper orthogonal decomposition (POD). We utilize each corresponding POD mode to detect features of the organized motions, namely, the vortex street, the shear layer and the near-wake bubble. We find that the vortex shedding modes contribute solely to the lift force, while the near-wake and shear layer modes play a dominant role in the drag force. We further examine the fundamental mechanism of this dynamical behaviour and propose a force decomposition technique via low-dimensional approximation. To elucidate the frequency lock-in, we systematically analyse the decomposed modes and their dynamical contributions to the force fluctuations for a range of reduced velocity at low Reynolds number laminar flow. These quantitative mode energy contributions demonstrate that the shear layer feeds the vorticity flux to the wake vortices and the near-wake bubble during the wake–body synchronization. Based on the decomposition of wake dynamics, we suggest an interaction cycle for the frequency lock-in during the wake–body interaction, which provides the interrelationship between the high-amplitude motion and the dominating wake features. Through our investigation of wake–body synchronization below critical 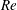 $Re$ range, we discover that the bluff body can undergo a synchronized high-amplitude vibration due to flexibility-induced unsteadiness. Owing to the wake turbulence at a moderate Reynolds number of
$Re$ range, we discover that the bluff body can undergo a synchronized high-amplitude vibration due to flexibility-induced unsteadiness. Owing to the wake turbulence at a moderate Reynolds number of 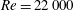 $Re=22\,000$, a distorted set of POD modes and the broadband energy distribution are observed, while the interaction cycle for the wake synchronization is found to be valid for the turbulent wake flow.
$Re=22\,000$, a distorted set of POD modes and the broadband energy distribution are observed, while the interaction cycle for the wake synchronization is found to be valid for the turbulent wake flow.