Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-22T21:43:22.719Z Has data issue: false hasContentIssue false
  • English
  • Français

Deceleration of droplets that glide along the free surface of a bath

Published online by Cambridge University Press:  19 August 2016

Jacob Hale Open the ORCID record for Jacob Hale [Opens in a new window]  and
Caleb Akers Open the ORCID record for Caleb Akers [Opens in a new window]
Jacob Hale*
Affiliation:
Department of Physics and Astronomy, DePauw University, Greencastle, IN 46135, USA
Caleb Akers
Affiliation:
Department of Physics and Astronomy, DePauw University, Greencastle, IN 46135, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A droplet obliquely impacting a bath surface of the same fluid can traverse along the interface while slowing at an exponential rate. The droplet rests on a thin film of air, deforms the bath surface creating a dimple and travels along the surface similarly to a wave pulse. Viscous coupling of the droplet and bath surfaces through the air film leads to viscous drag on the bath and perturbs the wave motion of the otherwise free surface. Even though the Reynolds numbers are greater than unity (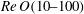$\mathit{Re}\,O(10{-}100)$), we show that the droplet’s deceleration is only due to viscous coupling through the air gap. The rate of deceleration is found to increase linearly with droplet diameter.

JFM classification

Drops and Bubbles: Breakup/coalescence Drops and Bubbles: Drops Interfacial Flows (free surface): Interfacial Flows (free surface)
Type
Papers
Information
Journal of Fluid Mechanics , Volume 803 , 25 September 2016 , pp. 313 - 331
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alghoul, S. K., Eastwick, C. N. & Hann, D. B. 2011 Normal droplet impact on horizontal moving films: an investigation of impact behaviour and regimes. Exp. Fluids 50, 1305–1316.CrossRefGoogle Scholar
Amarouchene, Y., Cristobal, G. & Kellay, H. 2001 Noncoalescing drops. Phys. Rev. Lett. 87 (20), 206104.CrossRefGoogle ScholarPubMed
Andersen, A., Madsen, J., Reichelt, C., Ahl, S. R., Lautrup, B., Ellegaard, C., Levinsen, M. T. & Bohr, T. 2015 Double-slit experiment with single wave-driven particles and its relation to quantum mechanics. Phys. Rev. E 92 (14), 013006.CrossRefGoogle ScholarPubMed
Aryafar, H. & Kavehpour, H. P. 2008 Hydrodynamic instabilities of viscous coalescing droplets. Phys. Rev. E 78 (4), 037302.CrossRefGoogle ScholarPubMed
Batchelor, G. K. 2010 An Introduction to Fluid Dynamics, 14th edn. Cambridge University Press.Google Scholar
Bouwhuis, W., van der Veen, R. C. A., Tran, T., Keij, D. L., Winkels, K. G., Peters, I. R., van der Meer, D., Sun, C., Snoeijer, J. H. & Lohse, D. 2012 Maximal air bubble entrainment at liquid-drop impact. Phys. Rev. Lett. 109 (4), 264501.CrossRefGoogle ScholarPubMed
Cai, Y. K. 1989 Phenomena of a liquid drop falling to a liquid surface. Exp. Fluids 7, 388–394.CrossRefGoogle Scholar
Charles, G. E. & Mason, S. G. 1960a The coalescence of liquid drops with flat liquid/liquid interfaces. J. Colloid Sci. 15, 236–267.CrossRefGoogle Scholar
Charles, G. E. & Mason, S. G. 1960b The mechanism of partial coalescence of liquid drops at liquid/liquid interfaces. J. Colloid Sci. 15, 105–122.CrossRefGoogle Scholar
Che, Z., Deygas, A. & Matar, O. K. 2015 Impact of droplets on inclined flowing liquid films. Phys. Rev. E 92 (13), 023032.CrossRefGoogle ScholarPubMed
Ching, B., Golay, M. W. & Johnson, T. J. 1984 Droplet impacts upon liquid surfaces. Science 226 (4674), 535–537.CrossRefGoogle ScholarPubMed
Couder, Y. & Fort, E. 2006 Single-particle diffraction and interference at a macroscopic scale. Phys. Rev. Lett. 97 (4), 154101.CrossRefGoogle Scholar
Couder, Y., Fort, E., Gautier, C.-H. & Boudaoud, A. 2005 From bouncing to floating: noncoalescence of drops on a fluid bath. Phys. Rev. Lett. 94 (4), 177801.CrossRefGoogle ScholarPubMed
Dell’Aversana, P., Banavar, J. R. & Koplik, J. 1996 Suppression of coalescence by shear and temperature gradients. Phys. Fluids 8 (1), 15–28.CrossRefGoogle Scholar
Esmailizadeh, L. & Mesler, R. 1986 Bubble entrainment with drops. J. Colloid Interface Sci. 110 (2), 561–574.CrossRefGoogle Scholar
Fort, E., Eddi, A., Boudaoud, A., Moukhtar, J. & Couder, Y. 2010 Path-memory induced quantization of classical orbits. Proc. Natl. Acad. Sci. USA 107 (41), 17515–17520.CrossRefGoogle Scholar
Gatne, K. P., Jog, M. A. & Manglik, R. M. 2009 Surfactant-induced modification of low Weber number droplet impact dynamics. Langmuir 25 (14), 8122–8130.CrossRefGoogle ScholarPubMed
Hahn, P.-S., den Chen, J. & Slattery, J. C. 1985 Effects of London-van der Waals forces on the thinning and rupture of a dimpled liquid film as a small drop or bubble approaches a fluid-fluid interface. AlChE J. 31 (12), 2026–2038.CrossRefGoogle Scholar
Hendrix, M. H., Bouwhuis, W., van der Meer, D., Lohse, D. & Snoeijer, J. H. 2016 Universal mechanism for air entrainment during liquid impact. J. Fluid Mech. 789, 708–725.CrossRefGoogle Scholar
Honey, E. M. & Kavehpour, H. P. 2006 Astonishing life of a coalescing drop on a free surface. Phys. Rev. E 73 (4), 027301.CrossRefGoogle ScholarPubMed
Hsiao, M., Lichter, S. & Quintero, L. G. 1988 The critical Weber number for vortex and jet formation for drops impinging on a liquid pool. Phys. Fluids 31 (12), 3560–3562.CrossRefGoogle Scholar
Jones, A. F. & Wilson, S. D. R. 1978 The film drainage problem in droplet coalescence. J. Fluid Mech. 87, 263–288.CrossRefGoogle Scholar
Keller, J. B. 1998 Surface tension force on a partly submerged body. Phys. Fluids 10 (11), 3009–3010.CrossRefGoogle Scholar
Klyuzhin, I. S., Ienna, F., Roeder, B., Wexler, A. & Pollack, G. H. 2010 Persisting water droplets on water surfaces. J. Phys. Chem. B 114, 14020–14027.CrossRefGoogle ScholarPubMed
Lhuissier, H., Tagawa, Y., Tran, T. & Sun, C. 2013 Levitation of a drop over a moving surface. J. Fluid Mech. 733 (14), R4.CrossRefGoogle Scholar
Mahadevan, L. & Pomeau, Y. 1999 Rolling droplets. Phys. Fluids 11 (9), 2449–2453.CrossRefGoogle Scholar
Mills, B. H., Saylor, J. R. & Testik, F. Y. 2011 An experimental study of Mesler entrainment on a surfactant-covered interface: the effect of drop shape and Weber number. AlChE J. 58 (1), 46–58.CrossRefGoogle Scholar
Neitzel, G. P. & Dell’Aversana, P. 2002 Noncoalescence and nonwetting behavior of liquids. Annu. Rev. Fluid Mech. 34, 267–289.CrossRefGoogle Scholar
Ooi, C. H., Vadivelu, R. K., John, J. St, Dao, D. V. & Nguyen, N.-T. 2015 Deformation of a floating liquid marble. Soft Matt. 11, 4576–4583.CrossRefGoogle ScholarPubMed
Pirat, C., Lebon, L., Fruleux, A., Roche, J.-S. & Limat, L. 2010 Gyroscopic instability of a drop trapped inside an inclined circular hydraulic jump. Phys. Rev. Lett. 105 (4), 084503.CrossRefGoogle ScholarPubMed
Ramkissoon, H. 1997 Slip flow past an approximate spheroid. Acta Mechanica 123, 227–233.CrossRefGoogle Scholar
Reynolds, O. 1881 On drops floating on the surface of water. Chem. News 44, 211–212.Google Scholar
Saylor, J. & Bounds, G. 2012 Experimental study of the role of the Weber and Capillary numbers on Mesler entrainment. AlChE J. 58 (12), 3841–3851.CrossRefGoogle Scholar
Sreenivas, K. R., De, P. K. & Arakeri, J. H. 1999 Levitation of a drop over a film flow. J. Fluid Mech. 380, 297–307.CrossRefGoogle Scholar
Thoroddsen, S. T. & Takehara, K. 2000 The coalescence cascade of a drop. Phys. Fluids 12 (6), 1265–1267.CrossRefGoogle Scholar
Tran, T., de Maleprade, H., Sun, C. & Lohse, D. 2013 Air entrainment during impact of droplets on liquid surfaces. J. Fluid Mech. 726 (11), R3.CrossRefGoogle Scholar
Walker, J. 1978 Drops of liquid can be made to float on liquid. What enables them to do so? Sci. Am. 238 (6), 151–158.CrossRefGoogle Scholar

Hale and Akers supplementary movie

Droplet impacting a bath. See figure 1b. t=tI.

Download Hale and Akers supplementary movie(Video)
Video 4.2 MB
Supplementary material: PDF

Hale and Akers supplementary material

Supplementary figures

Download Hale and Akers supplementary material(PDF)
PDF 409.5 KB

Hale and Akers supplementary movie

Motion of a long lifetime skirting droplet viewed from above. See figure 4b. t=ts.

Download Hale and Akers supplementary movie(Video)
Video 2.6 MB

Hale and Akers supplementary movie

Side view movie of a short lifetime skirting droplet. See figure 4a. t=ts.

Download Hale and Akers supplementary movie(Video)
Video 2.3 MB

Hale and Akers supplementary movie

Bottom-up and side views of droplet coalescence. See figure 6a and b. t=tr.

Download Hale and Akers supplementary movie(Video)
Video 1.3 MB

Hale and Akers supplementary movie

Top-down view of impacting droplet seeded with tracer particles. See figure 9a. t=tI.

Download Hale and Akers supplementary movie(Video)
Video 4 MB

Hale and Akers supplementary movie

Bottom-up view of skirting droplet seeded with tracer particles. See figure 10a. t=ts. Inset: diagram of side view of the droplet with the position of the tracer particle indicated by the arrow.

Download Hale and Akers supplementary movie(Video)
Video 10.1 MB