Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-17T15:17:39.376Z Has data issue: false hasContentIssue false
  • English
  • Français

Decaying capillary wave turbulence under broad-scale dissipation

Published online by Cambridge University Press:  09 September 2015

Yulin Pan  and
Dick K. P. Yue
Yulin Pan
Affiliation:
Department of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
Dick K. P. Yue*
Affiliation:
Department of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the freely decaying weak turbulence of capillary waves by direct numerical solution of the primitive Euler equations. By introducing a small amount of wave dissipation, measured by the viscosity magnitude 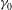${\it\gamma}_{0}$, we are able to recover phenomena observed in experiments that are not described by weak-turbulence theory (WTT), including the exponential modal decay and time variation of the width and power-law spectral slope ${\it\alpha}$ of the inertial range. In contrast to WTT, this problem also involves non-constant inter-modal energy transfer across the inertial range, which imposes a difficulty in quantifying and measuring the energy flux 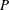$P$ associated with a certain power-law spectrum. We propose an effective and novel way to evaluate 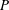$P$ in such cases by physically considering the unsteady effects of the spectrum and variation of the inter-modal energy transfer. Our results show the fundamental difference between the energy flux 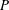$P$ and the total energy dissipation rate 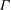${\it\Gamma}$, which is due to significant energy dissipation within the inertial range. This settles the previous debate on the measurement of 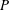$P$ which assumes the equivalence of the two. Based on our numerical data, we obtain a general form of the time-evolving inertial-range spectrum, where the parameters involved are functions of 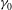${\it\gamma}_{0}$ only. The value of the spectral slope ${\it\alpha}$ at each time moment in the decay, however, is found to be uniquely related to the spectral magnitude at that time and irrespective of 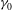${\it\gamma}_{0}$, in the range we consider. This physically reveals the dominant effect of nonlinear wave interaction in forming the power-law spectrum within the inertial range. The evolutions of the inertial-range energy are shown to be predicted by analytical integration of the evolving spectra for different values of 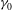${\it\gamma}_{0}$.

JFM classification

Waves/Free-surface Flows: Capillary waves Turbulent Flows: Turbulence theory Waves/Free-surface Flows: Waves/Free-surface Flows
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 780 , 10 October 2015 , R1
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Csanady, G. T. 2001 Air–Sea Interaction: Laws and Mechanisms. Cambridge University Press.Google Scholar
Deike, L., Bacri, J.-C. & Falcon, E. 2013 Nonlinear waves on the surface of a fluid covered by an elastic sheet. J. Fluid Mech. 733, 394–413.CrossRefGoogle Scholar
Deike, L., Berhanu, M. & Falcon, E. 2012 Decay of capillary wave turbulence. Phys. Rev. E 85 (6), 066311.CrossRefGoogle ScholarPubMed
Deike, L., Berhanu, M. & Falcon, E. 2014a Energy flux measurement from the dissipated energy in capillary wave turbulence. Phys. Rev. E 89 (6), 023003.Google Scholar
Deike, L., Daniel, F., Berhanu, M. & Falcon, E. 2014b Direct numerical simulations of capillary wave turbulence. Phys. Rev. Lett. 112 (1), 234501.CrossRefGoogle ScholarPubMed
Denissenko, P., Lukaschuk, S. & Nazarenko, S. 2007 Gravity wave turbulence in a laboratory flume. Phys. Rev. Lett. 99 (1), 014501.Google Scholar
Dyachenko, S., Newell, A. C., Pushkarev, A. & Zakharov, V. E. 1992 Optical turbulence: weak turbulence, condensates and collapsing filaments in the nonlinear Schrödinger equation. Physica D 57 (1), 96–160.Google Scholar
Falcon, E., Laroche, C. & Fauve, S. 2007 Observation of gravity–capillary wave turbulence. Phys. Rev. Lett. 98 (9), 94503.Google ScholarPubMed
Falkovich, G. E., Shapiro, I. Y. & Shtilman, L. 1995 Decay turbulence of capillary waves. Europhys. Lett. 29 (1), 1.CrossRefGoogle Scholar
Galtier, S., Nazarenko, S. V., Newell, A. C. & Pouquet, A. 2002 Anisotropic turbulence of shear-Alfvén waves. Astrophys. J. Lett. 564 (1), L49.Google Scholar
Kolmakov, G. V., Levchenko, A. A., Brazhnikov, M. Y., Mezhov-Deglin, L. P., Silchenko, A. N. & McClintock, P. V. E. 2004 Quasiadiabatic decay of capillary turbulence on the charged surface of liquid hydrogen. Phys. Rev. Lett. 93 (7), 074501.Google Scholar
Lvov, Y. V., Polzin, K. L & Tabak, E. G 2004 Energy spectra of the ocean’s internal wave field: theory and observations. Phys. Rev. Lett. 92 (12), 128501.Google Scholar
Martin, S. 2014 An Introduction to Ocean Remote Sensing. Cambridge University Press.CrossRefGoogle Scholar
Miquel, B., Alexakis, A. & Mordant, N. 2014 Role of dissipation in flexural wave turbulence: from experimental spectrum to Kolmogorov–Zakharov spectrum. Phys. Rev. E 89 (6), 062925.CrossRefGoogle ScholarPubMed
Miquel, B. & Mordant, N. 2011 Nonstationary wave turbulence in an elastic plate. Phys. Rev. Lett. 107 (3), 034501.Google Scholar
Newell, A. C. & Rumpf, B. 2011 Wave turbulence. Annu. Rev. Fluid Mech. 43, 59–78.Google Scholar
Pan, Y. & Yue, D. K. P. 2014 Direct numerical investigation of turbulence of capillary waves. Phys. Rev. Lett. 113 (9), 094501.Google Scholar
Phillips, O. M. 1985 Spectral and statistical properties of the equilibrium range in wind-generated gravity waves. J. Fluid Mech. 156, 505–531.Google Scholar
Pushkarev, A. N. & Zakharov, V. E. 1996 Turbulence of capillary waves. Phys. Rev. Lett. 76 (18), 3320–3323.CrossRefGoogle ScholarPubMed
Pushkarev, A. N. & Zakharov, V. E. 2000 Turbulence of capillary waves – theory and numerical simulation. Physica D 135 (1), 98–116.Google Scholar
Stiassnie, M., Agnon, Y. & Shemer, L. 1991 Fractal dimensions of random water surfaces. Physica D 47 (3), 341–352.Google Scholar
Xia, H., Shats, M. & Punzmann, H. 2010 Modulation instability and capillary wave turbulence. Europhys. Lett. 91 (1), 14002.Google Scholar
Zakharov, V. E. 1968 Stability of periodic waves of finite amplitude on the surface of a deep fluid. J. Appl. Mech. Tech. Phys. 9 (2), 190–194.Google Scholar
Zakharov, V. E. & Filonenko, N. N. 1966 Dokl. Akad. Nauk SSSR 170, 1292–1295.Google Scholar
Zakharov, V. E. & Filonenko, N. N. 1967 J. Appl. Mech. Tech. Phys. 8, 37–40.CrossRefGoogle Scholar
Zakharov, V. E., L’vov, V. S. & Falkovich, G. 1992 Kolmogorov spectra of turbulence: wave turbulence. Springer, ISBN: 3-540-54533-6.Google Scholar