Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-28T20:53:41.942Z Has data issue: false hasContentIssue false
  • English
  • Français

The decay of turbulence generated by a class of multiscale grids

Published online by Cambridge University Press:  12 October 2011

P. C. Valente  and
J. C. Vassilicos
P. C. Valente*
Affiliation:
Department of Aeronautics, Imperial College London, London SW7 2AZ, UK
J. C. Vassilicos*
Affiliation:
Department of Aeronautics, Imperial College London, London SW7 2AZ, UK
*
†Email addresses for correspondence: [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A new experimental investigation of decaying turbulence generated by a low-blockage space-filling fractal square grid is presented. We find agreement with previous works by Seoud & Vassilicos (Phys. Fluids, vol. 19, 2007, 105108) and Mazellier & Vassilicos (Phys. Fluids, vol. 22, 2010, 075101) but also extend the length of the assessed decay region and consolidate the results by repeating the experiments with different probes of increased spatial resolution. It is confirmed that this moderately high Reynolds number 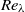turbulence (up to 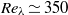here) does not follow the classical high Reynolds number scaling of the dissipation rate 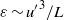and does not obey the equivalent proportionality between the Taylor-based Reynolds number and the ratio of integral scale 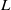to the Taylor microscale 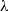. Instead we observe an approximate proportionality between 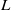and 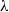during decay. This non-classical behaviour is investigated by studying how the energy spectra evolve during decay and examining how well they can be described by self-preserving single-length-scale forms. A detailed study of homogeneity and isotropy is also presented which reveals the presence of transverse energy transport and pressure transport in the part of the turbulence decay region where we take data (even though previous studies found mean flow and turbulence intensity profiles to be approximately homogeneous in much of the decay region). The exceptionally fast turbulence decay observed in the part of the decay region where we take data is consistent with the non-classical behaviour of the dissipation rate. Measurements with a regular square mesh grid as well as comparisons with active-grid experiments by Mydlarski & Warhaft (J. Fluid Mech., vol. 320, 1996, pp. 331–368) and Kang, Chester & Meveneau (J. Fluid Mech., vol. 480, 2003, pp. 129–160) are also presented to highlight the similarities and differences between these turbulent flows and the turbulence generated by our fractal square grid.

JFM classification

Turbulent Flows: Isotropic turbulence Turbulent Flows: Turbulence theory
Type
Papers
Information
Journal of Fluid Mechanics , Volume 687 , 25 November 2011 , pp. 300 - 340
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Antonia, R. A. 2003 On estimating mean and instantaneous turbulent energy dissipation rates with hot wires. Exp. Therm. Fluid Sci. 27, 151–157.CrossRefGoogle Scholar
2. Antonia, R. A., Smalley, R. J., Zhou, T., Anselmet, F. & Danaila, L. 2003 Similarity of energy structure functions in decaying homogeneous isotropic turbulence. J. Fluid Mech. 487, 245–269.CrossRefGoogle Scholar
3. Batchelor, G. K. 1953 The Theory of Homogeneous Turbulence. Cambridge University Press.Google Scholar
4. Batchelor, G. K. & Townsend, A. A. 1948 Decay of isotropic turbulence in the initial period. Proc. R. Soc. A 193 (1035), 539–558.Google Scholar
5. Burattini, P., Lavoie, P. & Antonia, R. A. 2005 On the normalized turbulent energy dissipation rate. Phys. Fluids 17, 098103.CrossRefGoogle Scholar
6. Comte-Bellot, G. & Corrsin, S. 1966 The use of a contraction to improve the isotropy of grid-generated turbulence. J. Fluid Mech. 25 (04), 657–682.CrossRefGoogle Scholar
7. Corrsin, S. 1963 Handbook der Physik. Springer.Google Scholar
8. Dimotakis, P. E. 2000 The mixing transition in turbulent flows. J. Fluid Mech. 409, 69–98.CrossRefGoogle Scholar
9. Ertunç, Ö., Özyilmaz, N., Lienhart, H., Durst, F. & Beronov, K. 2010 Homogeneity of turbulence generated by static-grid structures. J. Fluid Mech. 654 (1), 473–500.CrossRefGoogle Scholar
10. Freymuth, P. 1977 Frequency response and electronic testing for constant-temperature hot-wire anemometers. J. Phys. E: Sci. Instrum. 10, 705.CrossRefGoogle Scholar
11. Frisch, U. 1995 Turbulence: The Legacy of AN Kolmogorov. Cambridge University Press.CrossRefGoogle Scholar
12. Gamard, S. & George, W. K. 2000 Reynolds number dependence of energy spectra in the overlap region of isotropic turbulence. Flow Turbul. Combust. 63 (1), 443–477.CrossRefGoogle Scholar
13. Geipel, P., Henry Goh, K. H. & Lindstedt, R. P. 2010 Fractal-generated turbulence in opposed jet flows. Flow Turbul. Combust. 85 (3–4), 397–419.CrossRefGoogle Scholar
14. George, W. K. 1992 The decay of homogeneous isotropic turbulence. Phys. Fluids A 4 (7), 1492–1509.CrossRefGoogle Scholar
15. George, W. K. & Wang, H. 2009 The exponential decay of homogeneous turbulence. Phys. Fluids 21, 025108.CrossRefGoogle Scholar
16. Goto, S. & Vassilicos, J. C. 2009 The dissipation rate coefficient of turbulence is not universal and depends on the internal stagnation point structure. Phys. Fluids 21, 035104.CrossRefGoogle Scholar
17. Helland, K. N. & Van Atta, C. W. 1977 Spectral energy transfer in high Reynolds number turbulence. J. Fluid Mech. 79 (02), 337–359.CrossRefGoogle Scholar
18. Hurst, D. J. & Vassilicos, J. C. 2007 Scalings and decay of fractal-generated turbulence. Phys. Fluids 19, 035103.CrossRefGoogle Scholar
19. Ishida, T., Davidson, P. A. & Kaneda, Y. 2006 On the decay of isotropic turbulence. J. Fluid Mech. 564, 455–475.CrossRefGoogle Scholar
20. Jayesh, & Warhaft, Z. 1992 Probability distribution, conditional dissipation, and transport of passive temperature fluctuations in grid-generated turbulence. Phys. Fluids A 4, 2292.CrossRefGoogle Scholar
21. Kahalerras, H., Malecot, Y., Gagne, Y. & Castaing, B. 1998 Intermittency and Reynolds number. Phys. Fluids 10, 910.CrossRefGoogle Scholar
22. Kang, H., Chester, S. & Meneveau, C. 2003 Decaying turbulence in an active-grid-generated flow and comparisons with large-eddy simulation. J. Fluid Mech. 480, 129–160.CrossRefGoogle Scholar
23. Kármán, T. & Howarth, L. 1938 On the statistical theory of isotropic turbulence. Proc. R. Soc. A 164 (917), 192–215.Google Scholar
24. Kinzel, M., Wolf, M., Holzner, M., Lüthi, B., Tropea, C. & Kinzelbach, W. 2011 Simultaneous two-scale 3D-PTV measurements in turbulence under the influence of system rotation. Exp. Fluids 51 (1), 75–82.CrossRefGoogle Scholar
25. Kistler, A. L. & Vrebalovich, T. 1966 Grid turbulence at large Reynolds numbers. J. Fluid Mech. 26, 37–47.CrossRefGoogle Scholar
26. Kolmogorov, A. N. 1941 The local structure of turbulence in incompressible viscous fluid for very large Reynolds. C. R. Acad. Sci. U. R. S. S. 30, 301.Google Scholar
27. Krogstad, P. A˚. & Davidson, P. A. 2011 Freely decaying, homogenous turbulence generated by multi-scale grids. J. Fluid Mech. 680, 417–434.CrossRefGoogle Scholar
28. Laizet, S. & Vassilicos, J. C. 2011 Dns of fractal-generated turbulence. Flow Turbul. Combust doi:10.1007/s10494-011-9351-2.CrossRefGoogle Scholar
29. Lavoie, P., Djenidi, L. & Antonia, R. A. 2007 Effects of initial conditions in decaying turbulence generated by passive grids. J. Fluid Mech. 585, 395–420.CrossRefGoogle Scholar
30. Lesieur, M. 1997 Turbulence in Fluids. Kluwer Academic.CrossRefGoogle Scholar
31. Lumley, W. K. 1992 Some comments on turbulence. Phys. Fluids A 4 (2), 203–211.CrossRefGoogle Scholar
32. Makita, H. 1991 Realization of a large-scale turbulence field in a small wind tunnel. Fluid Dyn. Res. 8,.Google Scholar
33. Mathieu, J. & Scott, J. 2000 An Introduction to Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
34. Mazellier, N. & Vassilicos, J. C. 2008 The turbulence dissipation constant is not universal because of its universal dependence on large-scale flow topology. Phys. Fluids 20, 015101.CrossRefGoogle Scholar
35. Mazellier, N. & Vassilicos, J. C. 2010 Turbulence without Richardson–Kolmogorov cascade. Phys. Fluids 22, 075101.CrossRefGoogle Scholar
36. Mohamed, M. S. & LaRue, J. C. 1990 The decay power law in grid-generated turbulence. J. Fluid Mech. 219, 195–214.CrossRefGoogle Scholar
37. Mydlarski, L. & Warhaft, Z. 1996 On the onset of high-Reynolds-number grid-generated wind tunnel turbulence. J. Fluid Mech. 320, 331–368.CrossRefGoogle Scholar
38. Nagata, K., Suzuki, H., Sakai, Y., Hayase, T. & Kubo, T. 2008a Direct numerical simulation of turbulent mixing in grid-generated turbulence. Phys. Scr. 2008, 014054.CrossRefGoogle Scholar
39. Nagata, K., Suzuki, H., Sakai, Y., Hayase, T. & Kubo, T. 2008b DNS of passive scalar field with mean gradient in fractal-generated turbulence. Int. Rev. Phys. 2, 400.Google Scholar
40. Pearson, B. R., Krogstad, P.-A˚. & van de Water, W. 2002 Measurements of the turbulent energy dissipation rate. Phys. Fluids 14, 1288.CrossRefGoogle Scholar
41. Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
42. Queiros-Conde, D. & Vassilicos, J. C. 2001 Intermittency in Turbulent Flows and Other Dynamical Systems. Cambridge University Press.Google Scholar
43. Rotta, J. C. 1972 Turbulente Strömungen: eine Einführung in die Theorie und ihre Anwendung. B.G. Teubner.CrossRefGoogle Scholar
44. Sagaut, P. & Cambon, C. 2008 Homogeneous Turbulence Dynamics. Cambridge University Press.CrossRefGoogle Scholar
45. Schedvin, J., Stegen, G. R. & Gibson, C. H. 1974 Universal similarity at high grid Reynolds numbers. J. Fluid Mech. 65 (03), 561–579.CrossRefGoogle Scholar
46. Seoud, R. E. & Vassilicos, J. C. 2007 Dissipation and decay of fractal-generated turbulence. Phys. Fluids 19, 105108.CrossRefGoogle Scholar
47. Sreenivasan, K. R. 1984 On the scaling of the turbulence energy dissipation rate. Phys. Fluids 27, 1048.CrossRefGoogle Scholar
48. Sreenivasan, K. R. 1998 An update on the energy dissipation rate in isotropic turbulence. Phys. Fluids 10, 528.CrossRefGoogle Scholar
49. Stresing, R., Peinke, J., Seoud, R. E. & Vassilicos, J. C. 2010 Defining a new class of turbulent flows. Phy. Rev. Lett. 104 (19), 194501.CrossRefGoogle ScholarPubMed
50. Suzuki, H., Nagata, K., Sakai, Y. & Ukai, R. 2010 High-Schmidt-number scalar transfer in regular and fractal grid turbulence. Phys. Scr. 2010, 014069.CrossRefGoogle Scholar
51. Taylor, G. I. 1935 Statistical theory of turbulence. Proc. R. Soc. A 151 (873), 421–444.Google Scholar
52. Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT.CrossRefGoogle Scholar
53. Townsend, A. A. 1956 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
54. Uberoi, M. S. 1963 Energy transfer in isotropic turbulence. Phys. Fluids 6 (8), 1048–1056.CrossRefGoogle Scholar
55. Vassilicos, J. C. 2011 An infinity of possible invariants for decaying homogeneous turbulence. Phys. Lett. A 6, 1010–1013.CrossRefGoogle Scholar
56. Wang, H. & George, W. K. 2002 The integral scale in homogeneous isotropic turbulence. J. Fluid Mech. 459, 429–443.CrossRefGoogle Scholar