Published online by Cambridge University Press: 22 July 2019
Direct particle–fluid simulations of heavy spheres and ellipsoids interacting with decaying isotropic turbulence are conducted. This is the rigorous extension of the spherical particle analysis in Schneiders et al. (J. Fluid Mech., vol. 819, 2017, pp. 188–227) to 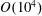 $O(10^{4})$ non-spherical particles. To the best of the authors’ knowledge, this represents the first particle-resolved study on turbulence modulation by non-spherical particles of near-Kolmogorov-scale size. The modulation of the turbulent flow is precisely captured by explicitly resolving the stresses acting on the fluid–particle interfaces. The decay rates of the fluid and particle kinetic energy are found to increase with the particle aspect ratio. This is due to the particle-induced dissipation rate and the direct transfer of kinetic energy, both of which can be substantially larger than for spherical particles depending on the particle orientation. The extra dissipation rate resulting from the translational and rotational particle motion is quantified to detail the impact of the particles on the fluid kinetic energy budget and the influence of the particle shape. It is demonstrated that the previously derived analytical model for the particle-induced dissipation rate of smaller particles is valid for the present cases albeit these involve significant finite-size effects. This generic expression allows us to assess the impact of individual inertial particles on the local energy balance independent of the particle shape and to quantify the share of the rotational particle motion in the kinetic energy budget. To enable the examination of this mechanistic model in particle-resolved simulations, a method is proposed to reconstruct the so-called undisturbed fluid velocity and fluid rotation rate close to a particle. The accuracy and robustness of the scheme are corroborated via a parameter study. The subsequent discussion emphasizes the necessity to account for the orientation-dependent drag and torque in Lagrangian point-particle models, including corrections for finite particle Reynolds numbers, to reproduce the local and global energy balance of the multiphase system.
$O(10^{4})$ non-spherical particles. To the best of the authors’ knowledge, this represents the first particle-resolved study on turbulence modulation by non-spherical particles of near-Kolmogorov-scale size. The modulation of the turbulent flow is precisely captured by explicitly resolving the stresses acting on the fluid–particle interfaces. The decay rates of the fluid and particle kinetic energy are found to increase with the particle aspect ratio. This is due to the particle-induced dissipation rate and the direct transfer of kinetic energy, both of which can be substantially larger than for spherical particles depending on the particle orientation. The extra dissipation rate resulting from the translational and rotational particle motion is quantified to detail the impact of the particles on the fluid kinetic energy budget and the influence of the particle shape. It is demonstrated that the previously derived analytical model for the particle-induced dissipation rate of smaller particles is valid for the present cases albeit these involve significant finite-size effects. This generic expression allows us to assess the impact of individual inertial particles on the local energy balance independent of the particle shape and to quantify the share of the rotational particle motion in the kinetic energy budget. To enable the examination of this mechanistic model in particle-resolved simulations, a method is proposed to reconstruct the so-called undisturbed fluid velocity and fluid rotation rate close to a particle. The accuracy and robustness of the scheme are corroborated via a parameter study. The subsequent discussion emphasizes the necessity to account for the orientation-dependent drag and torque in Lagrangian point-particle models, including corrections for finite particle Reynolds numbers, to reproduce the local and global energy balance of the multiphase system.