2.1. Flow physics: extreme vortex gust–airfoil interaction

As a model problem, we consider an extreme vortex gust–airfoil interaction around an NACA0012 airfoil with angles of attack $\alpha \in [20,60]^\circ$ at a chord-based Reynolds number of 100. The datasets are produced by fully resolved (direct) numerical simulations (Ham & Iaccarino Reference Ham and Iaccarino2004; Ham, Mattsson & Iaccarino Reference Ham, Mattsson and Iaccarino2006; Fukami & Taira Reference Fukami and Taira2023). The computational domain is set over $(x, y)/c \in [-15, 30] \times [-20, 20]$ with the leading edge of the wing positioned at the origin. Verification and validation have been performed extensively with previous studies (Liu et al. Reference Liu, Li, Zhang, Wang and Liu2012; Kurtulus Reference Kurtulus2015; Di Ilio et al. Reference Di Ilio, Chiappini, Ubertini, Bella and Succi2018; Zhong et al. Reference Zhong, Fukami, An and Taira2023).

Without the presence of a vortex gust, a wake at $\alpha = 20^\circ$ is steady while wakes at $\alpha \geq 30^\circ$ exhibit unsteady periodic shedding (limit-cycle oscillation). The current high $\alpha$ is motivated to model unsteady operating (base) conditions at the present Reynolds number. For the disturbed wake cases, an extremely strong vortex gust is introduced upstream of a wing at $x_0/c = -2$ and $y_0/c\equiv Y \in [-0.5, 0.5]$, as illustrated in figure 2. A Taylor vortex (Taylor Reference Taylor1918) is used to model the disturbance with a rotational velocity profile of

(2.1)\begin{equation} u_{\theta}=u_{\theta, max}{\dfrac{r}{R}}\exp\left[\dfrac{1}{2}\left({1-\dfrac{r^2}{R^2}}\right)\right] , \end{equation}

where $R$ is the radius at which $u_{\theta }$ reaches its maximum velocity $u_{\theta, max}$. To cover a variety of wake patterns in this study, the vortex gust is created by randomly chosen gust ratio $G \equiv u_{\theta,max}/u_\infty \in [-4,4]$, its size $D \equiv 2R/c \in [0.5, 2]$ and vertical position of the disturbance $Y$ relative to the wing. Note that the range of gust ratio $G$ considered herein is much larger than that traditionally thought of as flyable (Jones et al. Reference Jones, Cetiner and Smith2022).

Figure 2. (a) Velocity profile of the vortex gust. (b) An example vorticity field with a vortex gust. The parameters considered in the present study are also shown. The same colour scale of vorticity field visualization is hereafter used throughout the paper.

Let us exhibit in figure 3 the entire collection of lift responses in the present data with representative vortical field snapshots. Here, the convective time is set to zero when the centre of the vortex arrives at the leading edge of the airfoil. The present dataset includes 150 disturbed flow cases with 30 cases for each angle of attack. Strong vortex gusts induce a large excitation of aerodynamic forces within a very short time with highly nonlinear transient flow dynamics. Furthermore, the flow exhibits a variety of wake patterns depending on the parameter combination of the set-up including the vortex size, strength and initial position. Due to the nonlinear interaction between the vortex gust and a flow around an airfoil, massive flow separation can occur, creating additional vortical structures.

Figure 3. Entire collection of lift history over the parameter space of $(\alpha,G,D,Y)$ with representative vorticity fields. The vorticity field surrounded by the box (dashed line) is the undisturbed flow for each angle of attack. The dashed and solid lines in the lift curve correspond to the undisturbed case and a representative disturbed case, respectively. The light-blue circles in the parameter spaces correspond to the representative cases chosen for the vorticity field visualizations.

The gust ratio $G$ is one of the critical parameters that influence the flyability of air vehicles. Here, we examine the effect of $G$ on lift coefficient $C_L$ and vorticity field $\boldsymbol { \omega }$ for cases of $(\alpha,D,Y)=(40^\circ,0.5,0.1)$, as shown in figure 4. We consider $G=\pm 2$ and $\pm 4$ as representative examples. For the positive vortex gusts, lift first increases from the undisturbed state. Once the positive vortex gust impinges on the airfoil, the interaction between the gust and the airfoil wake causes massive separation, contributing to the decrease of the lift over $0< t<1$. In contrast, negative vortex disturbances decrease the lift first with subsequent lift value recovery towards that of the original limit-cycle case in a transient manner. Note that the transient lift generated by these vortices is very large compared with the undisturbed lift level. The fluctuation from the undisturbed lift generally increases as $|G|$ becomes large.

Figure 4. Dependence of lift coefficient $C_L$ and vorticity field $\boldsymbol { \omega }$ on the gust ratio $G$. The cases for $(\alpha,D,Y)=(40^\circ,0.5,0.1)$ with $G=\pm 2$ and $\pm 4$ are shown. The grey line in the lift response corresponds to the baseline (undisturbed) case.

It is also observed that the difference in $G$ of the positive gust cases causes the shift in timing for the secondary peak of $C_L$ from $t\approx 0.5$ ($G=2$) to $0.6$ ($G=4$). This is because the gust with $G=4$ interacts with the pre-existing negative vorticity on the suction side of the airfoil more strongly than that with $G=2$. As depicted with the vorticity snapshots at $t=0.125$, a stronger interaction with $G=4$ forms a larger negative vortex near the leading edge, compared with the case with $G=2$.

The dependence of the extreme aerodynamic response on the gust size is also investigated, as shown in figure 5. For comparison, we fix the angle of attack, gust ratio and vertical position $(\alpha, G, Y)=(40^\circ, 3.6, 0.1)$ while varying the gust size $D$ from 0.5 to 2. For all the disturbed cases with different $D$, the lift response exhibits the same trend of first increasing and then decreasing towards the original undisturbed case. The first lift peak appears earlier as the gust size increases since a larger vortex gust reaches the wing earlier, as presented in figure 5. While the gust of $D=0.5$ primarily interacts with the structures near the leading edge, the vortex gust of $D>1$ simultaneously impacts the leading and trailing edge vortices, exhibiting massive separation while newly generating large vortical structures.

Figure 5. Dependence of lift coefficient $C_L$ and vorticity field $\boldsymbol { \omega }$ on the gust size $D$. The cases for $(\alpha,G,Y)=(40^\circ,3.6,0.1)$ with $D=0.5$, 1, 1.5 and 2 are shown. The grey line in the lift response corresponds to the baseline (undisturbed) case.

The extreme vortex–airfoil interaction dynamics are also affected by the vortex position $Y$ in addition to gust ratio $G$ and gust size $D$. This causes the difference in the interaction of a vortex gust with the pre-existing vortical structures around a wing. To examine this point, we cover three vertical positions of $Y = (-0.3, 0, 0.3)$ for fixed parameters of $(\alpha, G, D)=(40^\circ, -2.2, 0.5)$, as presented in figure 6. The lift fluctuation for $Y=0.3$ from the undisturbed case is smaller than that for $Y=0$ and $-$0.3 since only the bottom half of the negative vortex gust impinges on the airfoil. By shifting the vortex position downward, a large portion of the gust interacts with the airfoil, producing a large variation of lift force. For $Y=-0.3$, the wing is largely affected by the negative vortex gust at the pressure side, experiencing a larger drop in lift force compared with the other two scenarios.

Figure 6. Dependence of lift coefficient $C_L$ and vorticity field $\boldsymbol { \omega }$ on the initial vertical position $Y$. The cases for $(\alpha,G,L)=(40^\circ,-2.2,0.5)$ with $Y=-0.3$, 0 and 0.3 are shown. The grey line in the lift response corresponds to the baseline (undisturbed) case.

We further note that the sharp lift responses from extreme vortex gust–airfoil interaction discussed above occur only within two convective times for almost all considered cases. While we easily recognize the difficulty of controlling air vehicles under such a significant variation in the lift force, it also implies that a controller for the present extreme aerodynamic flows needs to quickly modify the flow to attenuate the transient lift responses. This calls for a control technique that can react quickly.

2.2. Lift-augmented nonlinear autoencoder

Analysing the present extreme aerodynamic flows is challenging due to their complexity and nonlinearity. Furthermore, it is challenging to perform a large number of numerical simulations or experiments for studying the vortex–airfoil interaction across a large parameter space with finite resources. Hence, a model that universally captures the fundamental physics of extreme aerodynamics without necessitating expensive simulations and experiments would be beneficial.

In response, we have recently developed a lift-augmented nonlinear autoencoder (Fukami & Taira Reference Fukami and Taira2023) that can compress a collection of extreme aerodynamic vortical flow data across a large parameter space into only a few latent space variables while retaining the original vortex–airfoil interaction. An autoencoder is a neural-network-based model reduction technique (Hinton & Salakhutdinov Reference Hinton and Salakhutdinov2006). As illustrated in figure 7, an autoencoder is composed of an encoder ${\mathcal {F}}_e$ and a decoder ${\mathcal {F}}_d$ while having the bottleneck where the latent vector ${\boldsymbol { \xi }}$ is positioned. The autoencoder model is generally trained to output the same data as the given input data. In other words, the given high-dimensional input data can be compressed into the latent vector $\boldsymbol { \xi }$ if the autoencoder can successfully decode the original data.

Figure 7. Lift-augmented nonlinear autoencoder (Fukami & Taira Reference Fukami and Taira2023).

In this study, the discrete vorticity field $\boldsymbol { \omega }$ is compressed through the autoencoder such that

(2.2a–c)\begin{equation} {\boldsymbol{ \omega}}\approx{\mathcal{F}}(\boldsymbol{ \omega}) = {\mathcal{F}}_d({\mathcal{F}}_e({\boldsymbol{ \omega}})),\quad {\boldsymbol{ \xi}} = {\mathcal{F}}_e(\boldsymbol{ \omega}),\quad \boldsymbol{\omega} \approx \hat{\boldsymbol{\omega}} = {\mathcal{F}}_d({\boldsymbol{ \xi}}), \end{equation}

where $\hat {\boldsymbol {\omega }}$ is the decoded (reconstructed) vorticity field. The weights ${\boldsymbol {w}}$ inside a regular autoencoder are optimized by solving the following minimization problem:

(2.3)\begin{equation} {\boldsymbol{w}}^* = \underset{{\boldsymbol{w}}}{{\rm argmin}}\, \| {\boldsymbol{\omega}} - \hat{\boldsymbol{\omega}} \|_2=\underset{{\boldsymbol{w}}}{{\rm argmin}}\, \| {\boldsymbol{\omega}} - {\mathcal{F}}({\boldsymbol{\omega}; {\boldsymbol{w}}}) \|_2, \end{equation}

where ${\boldsymbol {w}}$ is the weights of the autoencoder. By using nonlinear activation functions inside the neural network, an autoencoder can nonlinearly compress high-dimensional data into a low-order subspace, which often achieves higher compression than linear techniques.

While nonlinear autoencoders can be used to compress a variety of vortical flow data (Omata & Shirayama Reference Omata and Shirayama2019; Xu & Duraisamy Reference Xu and Duraisamy2020; Fukami et al. Reference Fukami, Hasegawa, Nakamura, Morimoto and Fukagata2021a; Racca, Doan & Magri Reference Racca, Doan and Magri2023; Smith et al. Reference Smith, Fukami, Sedky, Jones and Taira2024), we have found that the regular formulation expressed in (2.3) does not produce a physically interpretable data distribution in the latent space (Fukami & Taira Reference Fukami and Taira2023). Extracting low-order coordinates associated with dominant aerodynamic features is important in considering not only the interpretation of extreme aerodynamic flows, but also downstream tasks such as developing control strategies. To facilitate the identification of a low-dimensional subspace from the aspect of aerodynamics, the proposed model referred to as a lift-augmented nonlinear autoencoder incorporates the lift coefficient $C_L(t)$.

In the present formulation, the additional branch network connected with the latent variables ${\boldsymbol { \xi }}(t)$ (lift decoder, the blue-shaded portion in figure 7) outputs $C_L(t)$. This side network enables ${\boldsymbol {w}}$ to be tuned to capture important vortical structures that are correlated lift due to $\varGamma \propto C_L$, where $\varGamma$ is circulation. This augmentation also helps to capture large transient lift caused by the present extreme vortex–airfoil interactions. The optimization for the weights inside the lift-augmented autoencoder is performed with

(2.4)\begin{equation} {\boldsymbol{w}}^* = \underset{{\boldsymbol{w}}}{{\rm argmin}}\,[\|{\boldsymbol{ \omega}}-\hat{\boldsymbol{ \omega}}\|_2 + \beta \|C_L - \hat{C}_L\|_2 ], \end{equation}

where $\beta$ balances the vorticity field and lift reconstruction loss terms. Here, the weights inside the main part and lift decoder are simultaneously optimized. For the present data-driven study, we use 1200 vorticity snapshots over 10.2 convective times per case. A subdomain of $(x, y)/c \in [-1.4, 4] \times [-1.2, 1.2]$ with spatial grid points $(N_x, N_y) = (240, 120)$ is extracted from the computational domain for the machine-learning analysis. Details on this autoencoder formulation are provided by Fukami & Taira (Reference Fukami and Taira2023).

2.3. Vortex–airfoil interaction on a low-dimensional manifold

With the nonlinear lift-augmented autoencoder, the entire collection of extreme aerodynamic vortical flows spanning over a large parameter space can be compressed into only three latent variables. The latent vectors ${\boldsymbol { \xi }}(t)$ in the present three-dimensional space are visualized in figure 8(a). Here, undisturbed baseline cases are shown in colour, while grey lines correspond to all the trajectories mapped from the disturbed vorticity flow field data. A variety of vortical flows with and without gust disturbances across five different angles of attack are considered. All of the extreme aerodynamic cases reside in the vicinity of the undisturbed base states, forming the cone-type structure. This cone shape is referred to as an inertial manifold to which the long-time dynamics converge (Foias, Manley & Temam Reference Foias, Manley and Temam1988; Temam Reference Temam1989; De Jesús & Graham Reference De Jesús and Graham2023). That is, the undisturbed periodic wake dynamics provide the backbone of the manifold with the extreme aerodynamic trajectories lying in the vicinity of this manifold in the three-dimensional latent space.

Figure 8. Extreme aerodynamic trajectories in (a) the three-dimensional latent space and (b) its two-dimensional view for the undisturbed baseline cases. (c) Undisturbed vorticity fields at $\theta = {\rm \pi}/4$ and ${\rm \pi}$ for $\alpha \in [30,60]^\circ$. The values inside each snapshot report the level of unsteadiness with $\sigma _{{\boldsymbol {\omega }}} = \|{\boldsymbol {\omega }}(t)-\bar {\boldsymbol {\omega }}\|_2/\|\bar {\boldsymbol {\omega }}\|_2$.

Here, let us detail the latent trajectories of the undisturbed flows. The latent vectors for the undisturbed flows across the angle of attack are aligned along the ${\xi }_3$ direction. The case of $\alpha = 20^\circ$ is mapped as a single dot while the other baseline cases with unsteady periodic shedding at $\alpha \geq 30^\circ$ exhibit cyclic trajectories. These observations in the latent space correspond to the steady flow at $\alpha = 20^\circ$ and unsteady limit-cycle oscillations at $\alpha \geq 30^\circ$ of vorticity fields.

The two-dimensional (projected) view of the latent space and representative vorticity fields for $\alpha \in [30, 60]^\circ$ at two different phases $\theta = {\rm \pi}/4$ and ${\rm \pi}$ are respectively shown in figure 8(b,c). The radius of each limit cycle for the undisturbed cases of $\alpha \geq 30^\circ$ increases with the angle of attack. They also correlate to the level of unsteadiness present in the vorticity field which we quantify as $\sigma _{{\boldsymbol {\omega }}} = \|{\boldsymbol {\omega }}(t)-\bar {\boldsymbol {\omega }}\|_2/\|\bar {\boldsymbol {\omega }}\|_2$, where $\bar {\boldsymbol {\omega }}$ is a time-averaged vorticity field. These values are listed in the representative snapshots for $\alpha \in [30, 60]^\circ$ in figure 8(c). As shown, the value of $\sigma _{{\boldsymbol {\omega }}}$ increases with the angle of attack. In other words, the increase of the radius is due to the increase in flow unsteadiness for each angle of attack case. Furthermore, undisturbed vorticity fields at each phase depicted in figure 8(c) present a similar wake shedding pattern across the angle of attack. These observations suggest that the undisturbed wakes can be successfully low-dimensionalized while preserving the phase (timing) and amplitude (fluctuation) in the original high-dimensional space.

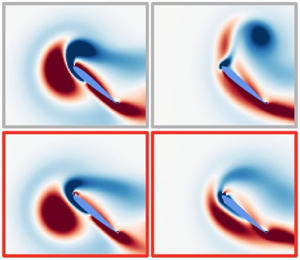
Next, let us focus on the latent space trajectories for the disturbed wake flows. All grey trajectories corresponding to extreme aerodynamic flows reside around the undisturbed orbits. To investigate the implication of low-dimensionalized extreme aerodynamic trajectories, we take an example case of $(G,D,Y) = (-2.8,1.5,0)$ for which a strong, large vortex gust impinges on an airfoil at $\alpha =60^\circ$. The latent variable trajectory and the reconstructed flow fields over time are also shown in figure 9. The value shown in each decoded flow contour reports the spatial $L_2$ reconstruction error norm $\varepsilon = \|{\boldsymbol {\omega }}-\hat {\boldsymbol {\omega }}\|_2/\|{\boldsymbol {\omega }}\|_2$. The vorticity field can be reconstructed well over time from the three variables with only approximately 20 % error. This level of error is reasonable for capturing the coherent structures accurately because the spatial $L_2$ norm is a strict comparative measure (Fukami, Fukagata & Taira Reference Fukami, Fukagata and Taira2019). While this feature of $L_2$ norm is useful for successful training of nonlinear machine-learning models, one can also consider the structural similarity index (SSIM) for assessing rotational and translational similarities of vortical flows (Wang et al. Reference Wang, Bovik, Sheikh and Simoncelli2004; Anantharaman et al. Reference Anantharaman, Feldkamp, Fukami and Taira2023). The error level here is similar across the parameter space. The lift decoder can also provide accurate estimates of lift coefficient $C_L$, corresponding to approximately 1 % $L_2$ error (Fukami & Taira Reference Fukami and Taira2023). This successful reconstruction indicates that the three-dimensional latent variables retain the essence of high-dimensional vortical flows without significant loss of key physics.

Figure 9. Extreme aerodynamic trajectories in the three-dimensional latent space and vortical flow snapshots for $(\alpha,G,D,Y) = (60^\circ,-2.8,1.5,0)$. The value inside of each decoded snapshot reports the $L_2$ spatial reconstruction error norm.

The extreme aerodynamic trajectories depicted in figure 9 exhibit the influence of strong vortex gusts on the flow. From the points (a) and (b) in figure 9, the latent vector dynamically rises and drops across the vertical direction in the latent space. This is likely because of the approach of negative vortex disturbance to the airfoil, which drastically changes the effective angle of attack $\alpha _{eff}$ (Anderson Reference Anderson1991; He et al. Reference He, Deparday, Siegel, Henning and Mulleners2020; Sedky, Jones & Lagor Reference Sedky, Jones and Lagor2020). In other words, the present lift-augmented autoencoder finds the relationship between extreme aerodynamic flows and lift force in a low-order manner. While the latent dimension is generally determined by checking the reconstruction performance of autoencoder, we note that the error behaviour of the present flows plateaus even if the latent dimension is increased as the flows are well approximated in the three-dimensional space with phase-amplitude ($\theta -r$) coordinates and the effective angle of attack.

The present physically interpretable low-dimensional representation of extreme aerodynamic flows is obtained due to the lift-augmented network while a regular autoencoder may not necessarily provide an understandable latent data distribution (Fukami & Taira Reference Fukami and Taira2023). We emphasize that expressing extreme disturbance effects about the undisturbed baseline dynamics is critical in developing flow control strategies because it enables us to identify the desired direction (or control objective) in the low-order coordinates to mitigate the strong impact of extreme vortex gusts.

3.1. Sparsity-promoting low-dimensional dynamical modelling

We model the dynamics of the latent vector ${\boldsymbol { \xi }}$ with a system of ordinary differential equations (ODEs) using sparse identification of nonlinear dynamics (SINDy; Brunton et al. Reference Brunton, Proctor and Kutz2016a). This data-driven technique identifies nonlinear model equations from given time-series data. Let us consider a dynamical system for the latent vector ${\boldsymbol { \xi }}(t)\in \mathbb {R}^3$,

(3.1) \begin{equation} \dot{\boldsymbol{\xi}}(t) = \boldsymbol{F} ( \boldsymbol{\xi}(t) ). \end{equation}

The temporally discretized data of $\boldsymbol {\xi }$ are collected to prepare a data matrix $\boldsymbol {\varXi }$,

(3.2) \begin{equation} \boldsymbol{\varXi}=\left(\begin{array}{@{}c@{}} \boldsymbol{\xi}^T(t_1) \\ \boldsymbol{\xi}^T(t_2) \\ \vdots \\ \boldsymbol{\xi}^T(t_m) \end{array}\right)=\left(\begin{array}{@{}ccc@{}} \xi_1(t_1) & \xi_2(t_1) & \xi_3(t_1) \\ \xi_1(t_2) & \xi_2(t_2) & \xi_3(t_2) \\ \vdots & \vdots & \vdots \\ \xi_1(t_m) & \xi_2(t_m) & \xi_3(t_m) \\ \end{array}\right) \in \mathbb{R}^{m \times 3}, \end{equation}

where $m$ is the number of snapshots. We also prepare a library matrix $\varPhi (\boldsymbol {\varXi })$ including nonlinear terms of $\boldsymbol {\varXi }$. This study uses sine and cosine functions for the library matrix construction,

(3.3)\begin{align} \varPhi(\boldsymbol{\varXi}) &= ( \sin({\boldsymbol{\varXi}}) \quad \sin({\boldsymbol{\varXi}}/2) \quad \sin({\boldsymbol{\varXi}}/4) \quad \sin({2{\boldsymbol{\varXi}}}) \quad \sin({4{\boldsymbol{\varXi}}}) \quad \cdots\nonumber\\ &\qquad \cos({2{\boldsymbol{\varXi}}}) \quad \cos({4{\boldsymbol{\varXi}}})) \in \mathbb{R}^{m \times n_l}, \end{align}

where we include sine and cosine functions of $\xi _i$, $\xi _i/2$, $\xi _i/4$, $2\xi _i$ and $4\xi _i$, resulting in the number of the library series $n_l$ to be 10. While polynomials constructed by given variables are often considered for the library matrix construction (Brunton et al. Reference Brunton, Proctor and Kutz2016a; Brunton, Proctor & Kutz Reference Brunton, Proctor and Kutz2016b; Kaiser, Kutz & Brunton Reference Kaiser, Kutz and Brunton2018; Li et al. Reference Li, Kaiser, Laima, Li, Brunton and Kutz2019), we have found that a trigonometric function-based library can provide a more accurate solution for the present problem. The SINDy-based modelling accuracy is determined by a set of factors including the dataset, the number of snapshots, the library functions and the optimization method (Fukami et al. Reference Fukami, Murata, Zhang and Fukagata2021c).

With the data matrix $\boldsymbol {\varXi }$ and the library matrix $\varPhi (\boldsymbol {\varXi })$, the latent dynamics is modelled as a form of ODE by determining the coefficients for each library term. A coefficient matrix $\varPsi$ is obtained by solving the following regression problem:

(3.4)\begin{equation} \dot{\boldsymbol{\varXi}}(t)=\varPhi (\boldsymbol{\varXi}) \varPsi, \end{equation}

with

(3.5)\begin{equation} \varPsi = (\psi_{\xi_1} \quad \psi_{\xi_2}\quad \psi_{\xi_3}) = \left(\begin{array}{@{}ccc@{}} \psi _{(\xi_1,1)} & \psi_{(\xi_2,1)} & \psi_{(\xi_3,1)} \\ \psi _{(\xi_1,2)} & \psi_{(\xi_2,2)} & \psi_{(\xi_3,2)} \\ \vdots & \vdots & \vdots \\ \psi _{(\xi_1,n_l)} & \psi_{(\xi_2,n_l)} & \psi_{(\xi_3,n_l)} \\ \end{array}\right). \end{equation}

In this study, the adaptive lasso (Zou Reference Zou2006; Fukami et al. Reference Fukami, Murata, Zhang and Fukagata2021c) is used to optimize the coefficient matrix $\varPsi$. Once we obtain an accurate low-dimensional dynamical model (3.4), the model is then used to perform the phase-amplitude reduction, which provides the optimal timing and location of control actuation to efficiently and quickly modify the dynamics.

3.2. Phase-amplitude reduction analysis

Here, let us introduce phase-amplitude reduction for a periodic, stable limit-cycle oscillator $\dot {\boldsymbol { \xi }}(t) = {\boldsymbol {F}}({\boldsymbol { \xi }}(t))$ obtained by the SINDy for each angle of attack case. It is assumed that this ODE has a stable limit-cycle solution ${\boldsymbol {\xi }}_0(t) = {\boldsymbol {\xi }}_0(t+T)$, where $T = 2{\rm \pi} /\omega _{\alpha }$ with the natural frequency $\omega _{\alpha }$ of the latent variable ${\boldsymbol { \xi }}$ for the undisturbed baseline case at each angle of attack $\alpha$. The natural frequency in the latent dynamics matches that in the high-dimensional wake dynamics as the encoder is applied to a time series of flow snapshots.

Given the aforementioned ODE system for the undisturbed system at each angle of attack, we define the phase and amplitude variables $\theta$ and $r$ of the latent system state ${\boldsymbol { \xi }}$, as illustrated in figures 8 and 10,

(3.6a,b)\begin{equation} \theta = \varTheta (\boldsymbol{ \xi}), \quad r = R(\boldsymbol{ \xi}), \end{equation}

where ${\varTheta }({\boldsymbol { \xi }})$ and $R({\boldsymbol { \xi }})$ are the phase and amplitude functions, respectively. Here, the phase and amplitude functions provide a global linearization of the original nonlinear dynamics in the basin of attraction of the limit cycle for each angle of attack. The phase function $\varTheta$ is defined to satisfy the condition that the phase $\theta$ increases with a frequency $\omega _\alpha$ at an angle of attack $\alpha$. Hence, the generalized phase dynamics is described as

(3.7)\begin{equation} \dot{\varTheta}({\boldsymbol{ \xi}}) = \langle \boldsymbol{\nabla}{\varTheta}({\boldsymbol{ \xi}}), \dot{\boldsymbol{ \xi}} \rangle = \langle \boldsymbol{\nabla}{\varTheta}({\boldsymbol{ \xi}}), {\boldsymbol{F}}({\boldsymbol{ \xi}}) \rangle = \omega_{\alpha}, \end{equation}

where $\langle {\boldsymbol {a}},{\boldsymbol {b}}\rangle = \sum _{i=1}^N a_i^*b_i$ is a scalar product.

Similarly, the generalized amplitude dynamics can also be derived with the assumption that $r$ exponentially decays to zero as ${\dot r}=\lambda r$ of the limit cycle, as presented in figure 10. Here, $\lambda$ denotes the decay rate given by the Floquet exponent, which characterizes the linear stability of ${\boldsymbol {\xi }}_0$. The connections among the natural frequency $\omega _\alpha$, phase sensitivity function $\varTheta$, Floquet exponents and amplitude sensitivity function $R$ ease the evaluation of phase and amplitude functions as discussed later. Although there are generally $n-1$ amplitudes for $n$-dimensional oscillators associated with the Floquet exponents $\lambda _i$, the dominant, slowest-decaying dynamics is sought whose exponent is denoted as $\lambda$ for simplicity (Nakao Reference Nakao2021). Thus, the amplitude function needs to satisfy

(3.8)\begin{equation} \dot{R}({\boldsymbol{ \xi}}) = \langle \boldsymbol{\nabla}{R}({\boldsymbol{ \xi}}), \dot{\boldsymbol{ \xi}} \rangle = \langle \boldsymbol{\nabla}{R}({\boldsymbol{ \xi}}), {\boldsymbol{F}}({\boldsymbol{ \xi}}) \rangle = \lambda R({\boldsymbol{\xi}}). \end{equation}

Now considering an external control input ${\boldsymbol {f}}(t)$ to the system, the oscillator dynamics is described as

(3.9)\begin{equation} \dot{\boldsymbol{ \xi}}(t) = {\boldsymbol{F}}({\boldsymbol{ \xi}}(t)) + {\boldsymbol{f}}(t). \end{equation}

For this perturbed system, the dynamics of phase $\theta$ and amplitude $r$ satisfy

(3.10a)$$\begin{gather} \dot{\theta}(t) = \omega_{\alpha} + \langle \boldsymbol{\nabla}\varTheta({\boldsymbol{ \xi}}(t)), {\boldsymbol{f}}(t) \rangle, \end{gather}$$

(3.10b)$$\begin{gather}\dot{r}(t) = \lambda r(t) + \langle \boldsymbol{\nabla} R ({\boldsymbol{ \xi}}(t)), {\boldsymbol{f}}(t) \rangle. \end{gather}$$

Here, we further assume that the control input ${\boldsymbol {f}}(t)$ is of ${O}(\epsilon )$ with $0 < \epsilon \ll 1$. These equations can be then approximated by neglecting the terms of order ${O}(\epsilon ^2)$,

(3.11a,b)\begin{equation} \dot{\theta} = \omega_{{\boldsymbol{ \alpha}}} + \langle {\boldsymbol{Z}}(\theta),{\boldsymbol{f}}(t) \rangle, \quad {\dot r} = \lambda r + \langle {\boldsymbol{Y}}(\theta),{\boldsymbol{f}}(t) \rangle, \end{equation}

where ${\boldsymbol {Z}}(\theta )=\boldsymbol {\nabla } \varTheta |_{{\boldsymbol { \xi }}={\boldsymbol {\xi }}_0(\theta )}$ and ${\boldsymbol {Y}}(\theta )=\boldsymbol {\nabla } {R}|_{{\boldsymbol { \xi }}={\boldsymbol {\xi }}_0(\theta )}$ are the phase and amplitude sensitivity functions, respectively, evaluated on the limit cycle for each angle of attack $\alpha$.

The phase sensitivity function ${\boldsymbol {Z}}(\theta )$ describes the sensitivity of the system phase and the amplitude sensitivity function ${\boldsymbol {Y}}(\theta )$ reveals the sensitivity of the system amplitude about the periodic orbit against external forcing. Although it is generally difficult to measure the phase and amplitude sensitivity functions, they can be obtained by assessing the left Floquet eigenvectors if a dynamical model is explicitly given (Kuramoto Reference Kuramoto1984; Takata et al. Reference Takata, Kato and Nakao2021).

If a low-order model is available through SINDy, we can derive from Floquet theory the phase and amplitude sensitivity functions ${\boldsymbol {Z}}(\theta )$ and ${\boldsymbol {Y}}(\theta )$, respectively. Here, we introduce the right and left Floquet eigenvectors ${\boldsymbol {U}}_i$, and ${\boldsymbol {V}}_i$ that are the $T$-periodic solutions,

(3.12a)$$\begin{gather} {\dot{\boldsymbol{U}}_i}(t) = [{\mathcal{J}}({\boldsymbol{ \xi}}_0(t)) - \lambda_i]{\boldsymbol{U}}_i(t), \end{gather}$$

(3.12b)$$\begin{gather}{\dot{\boldsymbol{V}}_i}(t) ={-}[{\mathcal{J}}({\boldsymbol{ \xi}}_0(t))^{{\dagger}} - \lambda_i^{\dagger}]{\boldsymbol{V}}_i(t) \end{gather}$$

for $i=0,1,\ldots, N-1$, where the superscript ${\dagger}$ represents the Hermitian conjugate and ${\mathcal {J}}$ is a $T$-periodic Jacobian matrix of $\boldsymbol {F}$ evaluated about ${\boldsymbol { \xi }}={\boldsymbol { \xi }}_0(t)$ (Ermentrout Reference Ermentrout1996; Brown, Moehlis & Holmes Reference Brown, Moehlis and Holmes2004; Shirasaka et al. Reference Shirasaka, Kurebayashi and Nakao2017; Kuramoto & Nakao Reference Kuramoto and Nakao2019). The phase sensitivity function ${\boldsymbol {Z}}(\theta )$ and the dominant amplitude sensitivity function ${\boldsymbol {Y}}(\theta )$ are then respectively expressed as

(3.13a,b)\begin{equation} {\boldsymbol{Z}}(\theta) = {\boldsymbol{V}}_0(\theta/\omega_{{\boldsymbol{ \alpha}}}), \quad {\boldsymbol{Y}}(\theta) = {\boldsymbol{V}}_1(\theta/\omega_{{\boldsymbol{ \alpha}}}) \end{equation}

for $0 \leq \theta < 2{\rm \pi}$. To obtain the phase and amplitude sensitivity functions ${\boldsymbol {Z}}(\theta )$ and ${\boldsymbol {Y}}(\theta )$, we first solve the ODE in the forward direction (i.e. the direct problem). The adjoint equation is then solved once the Jacobian at each phase for the time period is available so that ${\boldsymbol {U}}_1$ and ${\boldsymbol {V}}_1$ can be calculated (Takata et al. Reference Takata, Kato and Nakao2021).

3.3. Optimal fast flow control with amplitude constraint

Next, we consider feedforward control based on the phase and amplitude sensitivity functions. As illustrated in figure 10, suppressing the amplitude modulation in the low-order space can lead to the mitigation of the gust impact. Furthermore, since we now have a clear direction in the phase-amplitude space to mitigate the impact of gusts, it is possible to achieve fast synchronization with amplitude penalty such that the latent dynamics quickly returns to the undisturbed baseline dynamics while suppressing amplitude deviations (Harada et al. Reference Harada, Tanaka, Hankins and Kiss2010; Zlotnik et al. Reference Zlotnik, Nagao, Kiss and Li2016; Takata et al. Reference Takata, Kato and Nakao2021). For the vortex–airfoil interaction, synchronization at a higher frequency than the natural frequency with amplitude constraints would provide smaller vortical structures in a wake that are weaker than the undisturbed baseline case (Zhang & Haque Reference Zhang and Haque2022; Godavarthi et al. Reference Godavarthi, Kawamura and Taira2023), thereby swiftly reducing the vortex gust impact in the high-dimensional space. Hence, the objective of the present controller is to quickly attenuate the transient dynamics in the low-dimensional latent space ${\boldsymbol { \xi }}$ with phase locking. We obtain the actuation pattern to achieve the above objective by leveraging the optimal-synchronization waveform with amplitude suppression (Takata et al. Reference Takata, Kato and Nakao2021).

To begin with, let us introduce the relative phase (phase difference) $\phi (t) = \theta (t) - \omega _{{\boldsymbol {f}}}t$, where $\omega _{{\boldsymbol {f}}}$ is the forcing signal frequency. Assuming that the the control input ${\boldsymbol {f}}$ is given in the form of ${\boldsymbol {f}}(t) = {\boldsymbol {b}}_{{\boldsymbol { \xi }}}(\omega _{{\boldsymbol {f}}} t)$, the phase dynamics becomes

(3.14)\begin{equation} \dot{\theta} = {\omega}_{{\boldsymbol{ \alpha}}} + \langle {\boldsymbol{Z}}(\theta),{\boldsymbol{b}}_{{\boldsymbol{ \xi}}}(\omega_{{\boldsymbol{f}}} t) \rangle. \end{equation}

The dynamics of the relative phase is provided as

(3.15)\begin{equation} \dot{\phi}(t) = \Delta \varOmega + \langle {\boldsymbol{Z}}(\phi + \omega_{{\boldsymbol{f}}} t),{\boldsymbol{b}}_{{\boldsymbol{ \xi}}}(\omega_{{\boldsymbol{f}}} t) \rangle, \end{equation}

where $T_{{\boldsymbol {f}}}$ is a period of the periodic forcing input and $\Delta \varOmega = {\omega }_{\boldsymbol {\alpha}}-\omega _{{\boldsymbol {f}}}$. Since this equation is non-autonomous, we consider deriving an autonomous form by averaging over a period of forcing (Kuramoto Reference Kuramoto1984; Hoppensteadt & Izhikevich Reference Hoppensteadt and Izhikevich1997). The asymptotic behaviour of the relative phase dynamics can be approximated as

(3.16)\begin{equation} {\dot\phi}(t) = \Delta \varOmega + \varGamma(\phi), \quad \varGamma(\phi) =\dfrac{1}{T_f}\int_0^{T_{{\boldsymbol{f}}}} \langle {\boldsymbol{Z}}(\phi + \omega_{{\boldsymbol{f}}} \tau),{\boldsymbol{b}}_{{\boldsymbol{ \xi}}}(\omega_{{\boldsymbol{f}}} \tau) \rangle \,{\rm d}\tau, \end{equation}

where $\varGamma (\phi )$ is called the phase coupling function. Phase locking can be achieved if the relative phase becomes a constant such that $\dot \phi \rightarrow 0$. This phase locking is achieved when $- \max \varGamma (\phi ) < \Delta \varOmega < - \min \varGamma (\phi )$, uncovering the Arnold tongue that captures the condition for synchronization (Shim, Imboden & Mohanty Reference Shim, Imboden and Mohanty2007).

Next, we seek the optimal input to achieve the present control objective. The controller is first asked to synchronize the system to a forcing (target) frequency as quickly as possible. In other words, the rate of convergence of $\phi$ to a fixed, stable phase-locking point $\phi ^*$ needs to be maximized to satisfy $\dot {\phi ^*} = \Delta \varOmega + \varGamma (\phi ^*) = 0$. Furthermore, we also aim to suppress the excitation from the limit-cycle dynamics in the latent space.

To derive the periodic waveform that can satisfy the above conditions, the following cost function is used to formulate an optimization problem,

(3.17)\begin{align} {\mathcal{L}}({\boldsymbol{b}}_{{\boldsymbol{ \xi}}}) &={-} \varGamma^\prime (\phi^*) + \nu \left(P - \dfrac{1}{T_f}\int_0^{T_f} \langle {\boldsymbol{b}}_{{\boldsymbol{ \xi}}}(\omega_f\tau), {\boldsymbol{b}}_{{\boldsymbol{ \xi}}}(\omega_f\tau) \rangle \,{\rm d}\tau\right) \nonumber\\ &\quad + \mu (\Delta \varOmega + \varGamma (\phi^*)) - k \left(\dfrac{1}{T_f}\int_0^{T_f} |\langle {\boldsymbol{Y}} (\phi^*+\omega_{{\boldsymbol{f}}} \tau), {\boldsymbol{b}}_{{\boldsymbol{ \xi}}}(\omega_{{\boldsymbol{f}}} \tau)\rangle|^2 \,{\rm d}\tau\right), \end{align}

where $\nu$ and $\mu$ are Lagrangian multipliers, and $P$ is a constant satisfying $\sqrt {P} \sim {O}(\omega _{{\boldsymbol { \xi }}}\delta )$. The first term contributes to maximizing the synchronization rate $-\varGamma ^\prime (\phi ^*)$, the second term constrains the energy of actuation and the third term directly corresponds to the rate of convergence of $\phi$. In addition, the fourth term penalizes the excitation of the amplitude variable of the amplitude sensitivity function with the weight $k$.

The above optimization problem can be solved using the calculus of variations (Zlotnik et al. Reference Zlotnik, Chen, Kiss, Tanaka and Li2013; Takata et al. Reference Takata, Kato and Nakao2021) once we obtain the phase and amplitude sensitivity functions ${\boldsymbol {Z}}(\theta )$ and ${\boldsymbol {Y}}(\theta )$, respectively, through Floquet analysis for the latent evolution equation derived by SINDy. We can finally derive the optimal waveform as

(3.18)\begin{align} {\boldsymbol{b}}_{{\boldsymbol{ \xi}}}(\omega_{{\boldsymbol{f}}} t) &= \tfrac{1}{2} [ \nu {\boldsymbol{\mathsf{I}}} + k \,Re({\boldsymbol{Y}}(\phi^* + \omega_{{\boldsymbol{f}}} t) {{\boldsymbol{Y}}}^{\dagger} (\phi^* + \omega_{{\boldsymbol{f}}} t)) ]^{{-}1}\nonumber\\ &\quad \times[-{\boldsymbol{Z}}^\prime (\phi^* + \omega_{{\boldsymbol{f}}} t) + \mu {\boldsymbol{Z}}(\phi^* + \omega_{{\boldsymbol{f}}} t)], \end{align}

where ${\boldsymbol {Z}}^\prime$ is the derivative of phase sensitivity function with respect to phase and ${\boldsymbol{\mathsf{I}}}$ is an identity matrix. The weight value $k$ can be chosen either empirically or through the $L$-curve analysis (Hansen & O'Leary Reference Hansen and O'Leary1993) to balance the terms for fast synchronization and the amplitude constraint (Takata et al. Reference Takata, Kato and Nakao2021).

Because the optimal waveform in (3.18) is derived in the latent space, we need to convert it to forcing in the original physical space. Here, we derive the relationship of the perturbation between the latent and physical spaces, $\Delta {\boldsymbol { \xi }}$ and $\Delta {\boldsymbol { \omega }}$, respectively, for which we assume that the encoder ${\mathcal {F}}_e$ is continuously differentiable. To find such a perturbation $\Delta {\boldsymbol { \omega }}$ towards a particular direction in the physical space, we consider an input vorticity field ${\boldsymbol { \omega }}(t^*)$ with an arbitrary perturbation in the high-dimensional space $\Delta \tilde {\boldsymbol { \omega }}(t^*)$. The latent vector corresponding to the given vorticity field can be approximated with the Jacobian matrix ${\mathcal {J}}_{{\boldsymbol { \xi }}}(\boldsymbol { \omega })$ of ${\mathcal {F}}_e$ evaluated at time $t^*$ such that

(3.19)\begin{align} {\boldsymbol{ \xi}} + \Delta \tilde{\boldsymbol{ \xi}} &= {\mathcal{F}}_e ({\boldsymbol{ \omega}}+\Delta \tilde{\boldsymbol{ \omega}})\nonumber\\ & \simeq {\mathcal{F}}_e({\boldsymbol{ \omega}}) + {\mathcal{J}}_{{\boldsymbol{ \xi}}}(\boldsymbol{ \omega}) \Delta \tilde{\boldsymbol{ \omega}}. \end{align}

For the current three-dimensional latent-vector model, we consider giving three different patterns of perturbation to the physical flow field through $\Delta \tilde {\boldsymbol { \omega }}_m$ $(m=1,2,3)$. From (3.19), the deviation of the latent vector due to the perturbation in the physical space is expressed as

(3.20)\begin{equation} \Delta \tilde{\boldsymbol{ \xi}}_m = {\mathcal{J}}_{{\boldsymbol{ \xi}}}\Delta \tilde{\boldsymbol{ \omega}}_m. \end{equation}

For the unit vectors ${\boldsymbol {e}}_1$, ${\boldsymbol {e}}_2$ and ${\boldsymbol {e}}_3$ in the latent space, the relationship between the perturbation in each direction of the latent dynamics and the deviations in (3.20) is expressed through a coefficient matrix ${\boldsymbol{\mathsf{H}}} \in \mathbb {R}^{3\times 3}$,

(3.21) \begin{align} {\boldsymbol{\mathsf{I}}}& = ({\boldsymbol{e}}_1 \quad {\boldsymbol{e}}_2 \quad {\boldsymbol{e}}_3) =(\Delta \tilde{\boldsymbol{ \xi}}_1 \quad \Delta \tilde{\boldsymbol{ \xi}}_2 \quad \Delta \tilde{\boldsymbol{ \xi}}_3) \left(\begin{array}{@{}ccc@{}} {\mathsf{H}}_{11} & {\mathsf{H}}_{12} & {\mathsf{H}}_{13} \\ {\mathsf{H}}_{21} & {\mathsf{H}}_{22} & {\mathsf{H}}_{23} \\ {\mathsf{H}}_{31} & {\mathsf{H}}_{32} & {\mathsf{H}}_{33} \\ \end{array}\right)\nonumber\\ &= {\boldsymbol{D}}_{{\boldsymbol{ \xi}}} {\boldsymbol{\mathsf{H}}}. \end{align}

Hence, to individually perturb the latent system in the ${\boldsymbol {e}}_1$, ${\boldsymbol {e}}_2$ and ${\boldsymbol {e}}_3$ directions, the perturbation in the high-dimensional space towards a particular direction $\Delta {\boldsymbol { \omega }}_i$ $(i=1,2,3)$ is derived as

(3.22)\begin{equation} \Delta {\boldsymbol{ \omega}}_i = \sum_{j=1}^3 {\mathsf{H}}_{ji} \Delta \tilde{\boldsymbol{ \omega}}_j, \end{equation}

where the coefficient matrix can be determined as ${\boldsymbol{\mathsf{H}}} = {\boldsymbol {D}}^{-1}_{{\boldsymbol { \xi }}}$.

In the present study, the three different perturbations in the physical space (for (3.20)) are determined by a momentum injection at the leading edge of the airfoil at $45^\circ$, $90^\circ$ and $135^\circ$ relative to the local tangential direction. The actuation cost with the steady momentum coefficient $c_\mu = (\rho u_{jet}^2 \sigma )/(0.5 \rho u_\infty ^2 c)$, where $u_{jet}$ is the actuation velocity and $\sigma$ is the actuator width, is set to be 0.016. Here, three perturbations in (3.20) are individually derived at each $\theta$ over the periodic dynamics because the linearization in (3.19) is locally valid for small perturbation.

The perturbed flow fields and latent vectors (in (3.19)) and the derived forcing in the high-dimensional space corresponding to a perturbation for each direction in the latent space (in (3.22)) are shown in figure 11. The shift of latent vector shown as red, blue and green circles at each phase in figure 11(a) is quite small due to the small forcing input of $\Delta \tilde {\boldsymbol { \omega }}$. The magnitude and shape of forcing structures depicted in figure 11(b) vary over the dynamics and across the latent variables. The designed forcing is localized due to small forcing inputs for the three different patterns of $\Delta {\boldsymbol { \omega }}$. In this study, we examine how extreme aerodynamic flows can be controlled by such localized actuation spanning over a very small area with the assistance of optimal waveform analysis within a very short time duration.

Figure 11. Conversion from latent perturbation to forcing in the original space. (a) Examples of perturbed vorticity fields ${\boldsymbol { \omega }} + \Delta \omega$ and the corresponding latent vectors ${\boldsymbol { \xi }} + \Delta \tilde {\boldsymbol { \xi }}$. The colour used for the points in the latent space corresponds to the flame colour for the vorticity field. (b) Perturbation in the high-dimensional space towards a particular direction $\Delta {\boldsymbol { \omega }}_i$.

The identified relationship of the perturbation in the latent and high-dimensional spaces is also used to verify the phase sensitivity function ${\boldsymbol {Z}}(\theta )$ which is derived in (3.13) (details to be provided later with figure 13). Here, the designed perturbation ${\boldsymbol {K}}_\omega ({\boldsymbol {x}},t)= \epsilon {\boldsymbol {b}}_{{\boldsymbol { \xi }}}(t)\Delta {\boldsymbol { \omega }}({\boldsymbol {x}},t)$ is added to the right-hand side of the vorticity transport equation as

(3.23)\begin{equation} \partial_t {\boldsymbol{ \omega}}({\boldsymbol{x}},t) ={-}{\boldsymbol{u}}\boldsymbol{\cdot} \boldsymbol{\nabla} {\boldsymbol{ \omega}} +{Re}^{{-}1} \nabla^2 {\boldsymbol{ \omega}} + {\boldsymbol{K}}_{{\boldsymbol{ \omega}}}({\boldsymbol{x}},t), \end{equation}

where the designed perturbation in the velocity form ${\boldsymbol {K}}_{{\boldsymbol {u}}} = \boldsymbol {\nabla } \times {\boldsymbol {K}}_\omega$ is used for performing the present simulations (Kawamura et al. Reference Kawamura, Godavarthi and Taira2022). In the next section, we assess the amount of attenuation that can be achieved for extreme aerodynamic flows with the present localized forcing and the optimal waveform.